疑問と計画
をテイラー展開したものを解析接続の手法で定義域を拡げて行き,原点の周りを一周すると
だけズレるという話を聞いた.しかしそのズレというのが一体どのような理由で具体的にどのように出てくるのかについてはイメージし辛い.
今回,自分なりの方法で泥臭く確かめてみたので,その手順を記録しておこうと思う.まずは計画を聞いてもらうことにしよう.
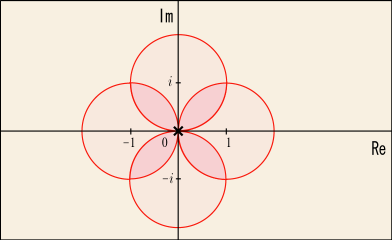
初めにを中心としたテイラー展開を考える.これは
に引っかかるので収束半径は 1 である.次に
を中心としたテイラー展開を考える.これも
に引っかかるので収束半径は 1 である.この二つの収束円には共通部分があるので,そこを頼りにして二つのテイラー展開が一致するように調整してやれそうだ.
次はを中心にしてテイラー展開したものを同じように繋げてやり,その次は
を中心にしたものと繋げてやる.これが最初の
を中心としたテイラー展開と矛盾なく繋がるかどうかが見どころである.
第 1 段階
を中心とした
のテイラー展開は次のように表されるのだった.
どこを中心にしてテイラー展開するにしても,この式に当てはめてゆけば良い.まずは
を中心にしたテイラー展開だが,次のように表せるだろう.
には無限多価性があって,本来ならば
であるのだが,ここではその中から敢えて
を採用したのである.
次にを中心にしたテイラー展開を書き出そう.
ここではまだ
の値を具体的には定めないでこのままにしておく.
さあ,次に何をするか?(2) 式と (3) 式が,両者に共通な定義域内で一致することを確かめたい.どちらも同じという関数をテイラー展開したものなのだから一致するのは当然のような気はするのだが,これだけ見た目が違うと,同じ
を代入したときに同じ値を返してくれるのかが不安になるのだ.
色々と検討してみたが,共通な点としてを使って検証するのがもっとも計算が楽だろうという結論に至った.なぜならば,この点は
であり,偏角が
であるから,
というとても簡単な値になることが既知だからである.複素平面上の対数関数は意外とややこしくて,他の点では規則性がつかみにくいのである.
では (2) 式と (3) 式にを代入してみよう.
さあ,困った.この右辺がどちらも同じ値になることをどうやって証明したらいいのだろう?計算が得意な人はすぐに分かるのかも知れない.しかし私は頑張って展開を試みたりしてパターンをつかもうとしたがうまく行かず,かなりの時間を費やしてしまった.実はこの
の点でやるしかないという諦めの境地にたどり着いたのは,そういう試行錯誤の末のことであった.
さて,私がどうやって解決したかというと,(5) 式のの部分については (4) 式をそのまま受け入れて
になるのだろうと考えることにしたのである.多分間違ってはいないだろう.(6) 式の
の計算についてはお手上げだったので,ネット上の数式計算機であるWolfram Alphaに丸投げしてみた.なんと!どうやって計算したのか分からないが,答を返してくれたのである.それに気を良くして,以後の計算は全てコンピュータに計算してもらった.
『sum (-1)^(n+1) (1/n) (1/i)^n ((sqrt(2)/2)(1+i)-i)^n, n=1 to infinity』と入れれば答を出してくれるのである.
その計算が本当に合っているかどうかを自力で確認する方法は後になって思いつくことになるのだが,とりあえずは結果を見てもらうことにしよう.
計算結果の列挙
結果を列挙したいのだが,などという書き方は分かりにくいし場所も食うので,複素平面上の 4 つの点を A, B, C, D と名付けることにしよう.
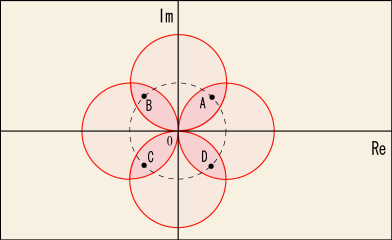
そして例えば,点を中心に展開したテイラー展開の
に例えば A の値を代入したものは
と表し,他も同じように表そう.
この (7) 式と (8) 式は先ほどの (5) 式,(6) 式と同じものである.
解決編
ここまでやれば知りたかったことが出てくるのはもうすぐだ.
解析接続のためには (7) 式と (8) 式は一致していなくてはならないはずだが,結果は違っているように見える.しかし (8) 式のの値をまだ決定していなかったのだった.これを
だとしておけば問題ないであろう.
(8) 式と (9) 式は全く同じテイラー展開の式にそれぞれ違う値を代入して作ったものだから,(9) 式で使っているは (8) と同じく
だとしておかないといけない.つまり (9) 式は
である.(9) 式と (10) 式は同じ値になっていなくてはならないはずなのでどうしたらいいか.(10) 式で使っている
の値を
とすればいいのである.
気持ちが焦る.続けよう.(10) 式と (11) 式で使っているは同じものだから,(11) 式の値は
だ.これと (12) 式が同じ値になっているはずなので,(12) 式で使われている
の値は
,いや,
だ.
結果が見えてきた.思ったような結果になりそうだ.あと少し.(12) 式と (13) 式で使っているは同じものだから,(13) 式の値は
.これと (14) 式が同じ値になるには・・・
でなくてはならない!
これが欲しかったものだ.初めにの周りに展開した時には
だと解釈していたのだった.しかし 1 周してきた時には
だとしておかないと解析接続ができないのである.これは元の
の周りのテイラー展開とは別のものである.解析接続で繋いできたひと続きの「同一の関数」ではあるが,一周してきたところで繋がる相手は元のテイラー展開ではなく,
だけズレた「別のテイラー展開」なのである.
検算
さて,コンピュータに教えてもらった値を使ってここまでの結果を出したわけだが,式を良く見れば,そんなに難しくはない気がしてくる.(7),(9),(11),(13) 式のの計算部分は,実は同一であることが変形で簡単に示せるではないか.
同様に,(8),(10),(12),(14) 式のの計算部分も同一であることが示せる.しかしそれらの値が
になることは直接は分からない.
それについては (14) 式のの部分を見ればいいのだ.それは無限多価性を考えずに
に点 D の値を代入したものと同じなので,
を既知だとすれば納得できる.










