物理数学：ローラン展開

ローラン展開の導出

複素平面でもテイラー展開ができるという大発見をしてしまったらそれだけで満足してしまいそうなものだが,天才たちはテイラー展開を導いた時のやり方を利用してさらに一歩先へ進んだのだ.テイラー展開は正則である領域でしか使えなかったが,孤立特異点を中心にして表す方法もあることを発見したのである.

コーシーの積分公式というものがあった. テイラー展開はこの式を変形することで導かれたのだった.この式の一周積分は f(w) が正則であるような領域で行う必要があるのである.すると,次の図のような妙なコースで積分してもそのコースに囲まれた内部が正則であることには変わりがないから,この公式は問題なく使えるわけだ.

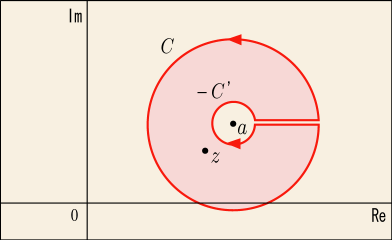
このコースは反時計回りの外側の円と時計回りの内側の円 -C' に分かれており,それらの間を往復するコースでの積分は打ち消し合うと考えて最初から無視するとして,(1) 式は次のように 2 つの項に分けて表されるだろう. 右辺第 2 項にある積分も反時計回りのコースで行うように統一しておきたいので全体をマイナスにして調整しておいた.

さて,前にテイラー展開の式を導いた時には,積分コース上を移動する変数は積分コースの内側の変数よりいつも外側にあったので,コースの内部に勝手に点を考えて, |w-a|>|z-a| という条件を満たすかのような変形を行うことができたのだった.(2) 式の第 1 項については今回もそれと同じ変形が出来るだろう.しかし第 2 項についてはの方が中心点に近くなるので大小関係が逆転し, |w-a|<|z-a| という条件で変形をしないといけなくなる.

要するに,第 1 項だけなら前に導いたテイラー展開と同じことなのだ.内側のコースを追加したことで,一体どんな結果が生まれるのだろうか.第 2 項だけ計算過程を書いてみよう.途中までは前にやったのとだいたい似たようなものだが,結果の見た目は大きく異なる. それで結局 (2) 式の全体では次のようにまとめられる. まだまとまっていないって？前にテイラー展開を導いた時には第 1 項に「グルサの公式」を当てはめてもう少し簡単な「いかにもテイラー展開」と分かる形にまでしたのだった.しかし今は意図があってそこまでしないで置いてある.とりあえず,この式をよく見て,パターンを把握してみて欲しいのである.

前にコーシーの積分公式を導いた回の冒頭のところで,「外側の反時計回りコースでの積分は,内側の反時計回りコースの積分で代用できる」と説明したことがある.もちろん,内側のコースを外側のコースで代用することができると言っても同じことだ.(3) 式の第 2 項の積分の経路は今はとなっているが,図を見てもらえば分かるようにとの間に挟まれた領域は正則であるので,これを第 1 項の積分で使っている経路と同じものに替えても結果は変わらない.これで,もっとまとめられるのではないだろうか？のの範囲を負にまで拡張してからまでにしたら一つのパターンに収まってしまった.関数 f(z) をこのような形に展開することを「ローラン展開」と呼ぶ.もう少し分かりやすく書くと,ローラン展開は要するに,こんな形になっているのである. ここで $a_{n}$ と表現したものは定数であり,次のようにして計算できる. (5) 式の 1 行目を「主要部」と呼び,2 行目を「正則部」と呼ぶ.

まだ何が何だか分からないかも知れない.導出が出来ても意味が把握できてないということはよくある話だ.この展開の意味についてはこれから説明するので安心してほしい.

誤解しないための予防線

ローラン展開とは何だろう？関数 f(z) をテイラー展開の形にしたり,ローラン展開の形にしたり,どちらの形にでも好みに応じて展開できるということだろうか？いやいや,そうではない.正則な関数はローラン展開しようとしてもテイラー展開と同じものになってしまうのである.

本当にそうなっているのか確認してみよう.テイラー展開と同じというためには (5) 式の 1 行目,「ローラン展開の主要部」と呼ばれる部分が邪魔である.つまり,(6) 式で表されている a_n が,が負の場合には 0 になっていないとおかしい.(6) 式を次のように書いた方が分かり良いだろう. n≦-1 なら (-n-1)≧0 であるので, f(z) が正則ならばこの被積分関数の全体も正則であって一周積分は 0 になってしまう.つまり n≦-1 では $a_{n}$ はすべて 0 であり, n≧0 では $a_{n}$ はグルサの公式で書き換えられて,(5) 式はテイラー展開そのものになる.

ローラン展開はテイラー展開を含んだ拡張版なのである.

すると,関数 f(z) が正則ならテイラー展開になり,関数 f(z) が特異点を持つようならローラン展開になる,という理解をしておけばいいだろうか？いや・・・,まだ少し言葉が足りなくて正確でない気がする.なぜなら,特異点を持つような関数であってもテイラー展開はできたではないか.点を中心にした円形の領域内で関数が正則なら,その範囲内でテイラー展開は収束したのである.それより外側には特異点があっても良かった.今回のローラン展開でも,そういう状況なら結果の式はテイラー展開になるのである.ということは,どう表現すればもっと正確になるだろう？

我々に選べるのは,「どの点を中心にして」「どの範囲で」展開するかということだけである.(6) 式を見ると分かるが,展開の中心であるの値と積分の円形コースの選択が我々の手に残されている.選んだ円形コースの内側に特異点が含まれていればローラン展開の形になり,選んだ円形コースの内側の全域が正則であれば自動的にテイラー展開の形になる.どちらの形で展開されることになるかについては我々には選べない.それは勝手に決まるのだ.

その辺りの状況はローラン展開の具体例を幾つか見てもらった方が分かり易いのだが,まだ幾つか説明したいことがあるので後回しにしておこう.

なぜ後回しにするかというと,ローラン展開を具体的に行うために (6) 式を使って各係数をいちいち計算するのは骨が折れる作業だからである.もっと簡単にローラン展開を実行する方法があるのだ.

テイラー展開と違って,ローラン展開は特異点を中心にして展開することも出来る.なるほど,グルサの公式というのは点での f(z) の微分を表す式だったから,が特異点になっている場合には微分の値など定まるはずもなく,グルサの公式は当てはめることができない.先ほどローラン展開の式を導く際にあえてグルサの公式を一律に当てはめなかった意図はそこにあったわけだ.

留数

さて,(6) 式で表されたローラン展開の係数 $a_{n}$ は,変数を含んでいない.つまり,これを実際に計算すれば,何らかの定数としての値が得られるはずである.このことは大変重要なことを教えてくれている.

つまり,今やほとんどの関数は・・・そう,幾つかの孤立特異点を持っていたとしても・・・ (5) 式の形で表されると分かったわけで, f(z) を積分しようとする場合には (5) 式の形にしたものを項別に積分すれば良いということになる.その際に, $a_{n}$ は全て定数と見なして構わないわけだ.これはとてもやりやすいのではなかろうか？

さらに都合が良いことがある.例えば, z=a に特異点を持つような関数 f(z) をの周りを回るようなコースで一周積分をすることを考えてみよう.これまではこのような積分計算はなるべく避けて,幾つかの特別な場合だけを考えてきたのだった.

f(z) を (5) 式のように表現しておいたとする.このとき, $a_{0}$ 以降の項,それは「正則部」と呼ばれていたが,それについては全て正則なので 0 になることが分かっているではないか！計算がかなり省けることになる.

あとは 1/(z-a)^n という形の関数をの周りで一周積分したときにどうなるかを公式として知っていればいいのだ.いや待てよ, n=1 の場合については以前にやったことがあるのだった.確か, 2πi になるのだ.すると n≧2 の場合についてだけ確かめればいいだろう.点は特異点であり,その周囲を一周するような経路を考える必要がある.そしてその経路は一周してさえいればどんな形であろうと結果は同じ値になるというのは前にも説明した通りだ.先ほども「外側の反時計回りコースでの積分は,内側の反時計回りコースの積分で代用できる」と言っていた原理のことである.だから経路をとしておこう.これは点を中心にして半径の円形を反時計回りに回るコースだ. ん？0・・・？確かにゼロだ.

ということは,(5) 式を特異点の周りで積分した結果として残るのは $a_{-1}/(z-a)$ の項からの効果だけだというのか！？つまり,関数 f(z) をその孤立特異点 z=a の周りで一周積分した時の結果は $2πia_{-1}$ と表されると！？ローラン展開をした時の係数の中で,一周積分して残るのは $a_{-1}$ だけだというので, $a_{-1}$ のことを「留数（りゅうすう）」と呼ぶ.留まる数,残る数,という意味である.

留数はどこを中心にして展開したかによって値が変わるものなので,いつも $a_{-1}$ と表していたのでは不便なことが出てくる.それで関数と中心点を指定して, Res[a,f(z)] のように表すことがある.わざわざ関数を指定しなくても通じる場合には Res(a) と書いてもいいだろう.その辺りは教科書によって様々であるが,だいたい似たような書き方にはなっている.

留数の計算方法

孤立特異点の周りでの積分を計算するときには留数を求めるのがとても重要であるということが分かってもらえたと思う.留数を求めるにはどうすればいいだろうか？(6) 式に n=-1 を当てはめてみよう. ナンジャコリャ？すごく当たり前の結果でしかないじゃないか. f(z) の一周積分を楽に計算するために留数が欲しいというのに,それを求めるためには f(z) の一周積分を計算する必要があるとは何とバカバカしい話だ！

この方法は使いものにならない.別の事を考えよう.

実はわざわざ (6) 式を使わなくてもローラン展開する方法が幾つかある.何とかして自力でローラン展開の形に変形してやれば,それがローラン展開なのである.・・・と言いたいところだが,少し違う.それがややこしいところだ.

(6) 式に頼らないローラン展開の具体例を少しやって見せよう.

具体例（その1）

次の関数をローラン展開してみよう. 正則な点を中心にして展開してみてもテイラー展開と同じになってしまって面白くなさそうなので,ここでは孤立特異点を中心にして展開してみたい.この関数の特異点は見てすぐ分かるように z=1 と z=3 である.もちろん,どちらを中心にして展開するかによって結果は異なる.どちらでもいいのだが,ここでは z=1 を選んでやってみよう.

ところで,関数 f(z) をローラン展開したものを使うとき,当然だがに代入する値は正則な領域から選ばなければならない.しかしながら,我々はローラン展開の式を導き出す時に等比級数が収束する条件を使っているから,正則な領域を円形で分割して指定する必要がある.分かりにくいだろうから今の状況を図にしてみよう.

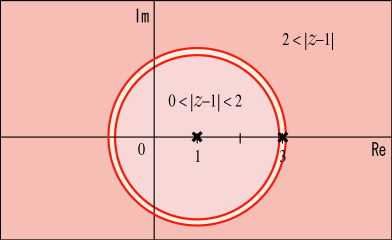
z=1 から最も近い特異点までの距離は 2 である.だから z=1 を中心とする半径 2 未満の領域は正則であると言えそうだ.いや,正しくはそこから z=1 の点を除く必要がある.すなわち 0<|z-1|<2 という条件を満たす領域が正則だと言えそうである.またこの他に,半径が 2 より大きい領域でも正則である.それは |z-1|>2 と書けるだろう.ところが,ちょうど |z-1|=2 となる円上には特異点 z=3 が乗っているので,残念ながらこの条件に合うはローラン展開には代入できない.

というわけで,2 つの領域でローラン展開が可能だと言えそうだ.

まずは,

を満たす領域でのローラン展開を実行してみよう.

定石として,次のように部分分数分解を行う.高校でも良くやっただろう. 第 1 項はすでにローラン展開の項の一部になりそうなので放っておいて,第 2 項にある 1/(z-3) から z-1 という要素を抽出する作業に取り掛かろう. 難しそうに見えるがそうでもない.最後は分母を 2 で割りたいと思って結果としてこうなっただけである.何がやりたいかと言うと,すでに複素平面上でのテイラー展開やローラン展開の導出でもお馴染みの,等比級数の公式を使える形になるように狙っているのである. 今は |z-1|<2 という条件でやっているのだから, | (z-1)/2 |<1 が成り立っており,この公式が使えそうだ. いつでもこんなに都合よく変形できるはずがないと思うかも知れないが,毎回,なぜかうまく行くのである.以上の結果を総合すると,次のようになるだろう. これが一つ目の答だ. 1/(z-1) の係数のことを留数と言うのだったから,留数は -1/2 である.

次に

を満たす範囲でのローラン展開を計算してみよう.

実は途中までは同じなのだ.見覚えのあるところから分岐してみよう. 難しそうに見えるがそうでもない.最後は分母を z-1 で割りたいと思って結果としてこうなっただけである.何がやりたいかと言うと,やはりさっきと同じ公式に当てはめたいのである.今は |z-1|>2 なのだから, | 2/(z-1) |<1 を満たしており,公式に当てはめることが出来る. 以上の結果を総合すると,次のようになるだろう. これが二つ目の答だ.さて,今回の留数は 0 だと言って良いだろうか.

いや,言わないのだ.先ほどは詳しく書かなかったが,実は留数というのは特異点のごく周辺の正則な領域で展開した場合の係数 $a_{-1}$ のことを指している.だからこちらの領域で行ったローラン展開の係数は留数とは呼ばないのである.

具体例（その2）

これだけではまだ「完全に分かった！」という感じにはなれないだろうから他にも幾つかの例をやってみよう.大切なことは先ほど説明し終えているので,もう少し短く終われるだろう.先ほどと同じ式を使う. 先ほどは「正則な点を中心にして展開してみてもテイラー展開と同じになってしまって面白くなさそう」と書いたのだが,どうやらそうでもなさそうな気がしてきた.それで z=0 を中心にして展開してみる.状況は次の図のようになっている.

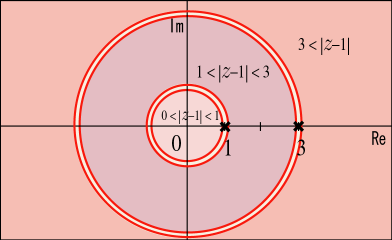
要するにローラン展開の使える領域が,次の 3 つに分類できるわけで,ただのテイラー展開とは違ったことが見れそうだ. まずは定石として部分分数分解を行う.前の例と同じだ. そして,このそれぞれの項のカッコの中を展開してやる.先ほどの例でも使った公式が使えるだろう.

初めは領域 I から行こう. 2 行目の式では z/3 という部分があるが,今は |z|<1 という条件でやっているのであり, |z/3|<1 を「十分すぎるほど」満たしているので同じ公式が使えたのである.結果をまとめると次のようになる. なるほど,の冪乗の項だけが並んでいて,確かにテイラー展開のような形だ.

次は領域 II である.公式に当てはまるようにするにはどうしたら良いかと迷うかもしれないが,先ほどの例でも出てきたパターンを使うだけである. 結果をまとめると次のようになる. の冪乗の項だけでなく,負冪の項が出てくる形になった.いかにもローラン展開といった感じだ.

最後に領域 III である. 結果をまとめると次のようになる. 負冪の項だけになった.だからと言って特に付け加えて言うこともない.

まぁ,こんな具合にすればいいというだけの例だ.

いや,一言付け加えておきたい・・・.先ほどは「ローラン展開はテイラー展開を含んだ拡張版」などと表現したが,ひょっとして,ローラン展開はそれよりももっとすごいものなんじゃないだろうか.テイラー展開ではカバーできなかった範囲でも収束するように展開できるというのだから,もう万能じゃないか！

具体例（その3）

もう少しうまく行かなさそうな例を試してみようか.どんな関数が来ても自力で展開できるという自信を付けてもらいたいのである.とは言うものの複雑なものはそれなりに難しいし,どんな関数でも必ずうまく展開できるテクニックがあるというわけでもない.

ここまでは領域を分けてやっていたが,時間がかかるので肝心な部分だけにしておこう.我々の目的は留数を求めることであり,その為には特異点の周囲でのローラン展開を導きさえすれば良いのである.我々が留数を求めるのは,一つの特異点だけを周るコースでの複素積分を簡単に実行するためである.だからそのような領域で関数がどういう展開で表せるかということに強い関心があるわけだ.

次のような例を試してみよう. 特異点は z=i と z=-1 の二つ.両方やってみたいが,ここでは z=i の方を選んでみよう.

二つの特異点の間の距離は |-1-i| であるから,それより小さい半径内で展開する.条件は 0<|z-i|<|1+i| である.関数の中にある 1/(z-i)^2 の部分はすでに展開後の形に似ているから残しておいて, 1/(z+1) の方を展開してやる. ここまでの例と少し違うのは,等比級数の公式に当てはめるためにマイナスをわざわざ追加しているところだろうか.そのために,結果には正の項と負の項が交互に現れることになっている.等比級数の公式はこういう使い方をしてもいいわけだ.

ちょっと分かりにくいが,主要部が 2 項だけで,残りは正則部が無限に続く形になっているところにも注目しておいて欲しい.主要部が何次の項まであるかによって特異点が分類されることになるのである.それについては次回話そう.

具体例（その4）

前の例と同じ関数を使う. 次は z=-1 の方でやってみよう.つまり (z+1) の冪として展開してやりたいのである. 1/(z+1) の方はすでにその形になっているのでしばらく置いておくとして, 1/(z-i)^2 の方についてはどうやって展開したら (z+1) の冪で表せるというのだろう？

ここは,次のようなテイラー展開の公式を利用するのである. この右辺の収束半径は 1 である.つまり |x|<1 の範囲で使える公式である.今回は k=2 の場合を使うことになる.やってみよう. 結果は割りとどうでもいい.途中で放り出そうと思ったくらいだが,意外とまとまりそうだったので頑張って最後までやってみた.ここではどんな公式を使ったらいいかを伝えたかっただけである.

具体例（その5）

ここまでの例は全て分子に 1 を持ってきていた.なるべく説明を楽にしたかったためである.もし分子に変数を含む場合にはどうなるだろう. あまり心配は要らない.次のように変形して分子の次数を下げてやればいい.高校の数学でもこれくらいのことをやるだろう. あとはここまでの話と同じになる.分数の外へ掃き出した z-2 については,もし (z-1) の冪に展開したいのなら z-2=-1+(z-1) と変形してやればいいのだし, (z+3) の冪に展開したいのなら z-2=-5+(z+3) と変形してやればいい.

今の例では分数の外へ掃き出した関数が z-2 という単純なものだったが,さらに次数が高い複雑なものだったらどうしたら良いだろう？例えば,複雑なものになると次のようなものが出てくる可能性もあるわけだ. これを (z+3) の冪で表せとなったらどうするか？

まぁ,計算は面倒だがそんなに問題ではない.新しい変数を導入して t=z+3 と置いてやればいいのだ.これを変形すれば z=t-3 になるので,これをさっきの式に代入してやり・・・これを全て展開する. そしてこれを元の変数に戻せば出来上がりだ. 調子に乗って次数を増やし過ぎたせいで大変なことになったが,技術的には難しい作業ではない.

具体例（その6）

ここまでの例は「整式」ばかりであった.「もっとこう,ここまでの具体例とは全く違った形の関数が出てきた場合にはどう対処したらいいんだ？」という疑問を持った人のために,こんな例題はどうだろうか？特異点が z=i の一つだけなので,そこを中心に展開してみよう.次のように変形すればいい. e^i というのは $e^{iθ}$ に当てはめると θ=1 であって, θ=π で180°なのだからだいたい 57.3°くらいだ.具体的数値としては 0.54+0.84i くらいの点を意味している.ここではただの複素数の定数値ということで e^i のままにしておこう.

また e^z という関数をテイラー展開したものは, であるが,これは複素平面の全域で収束するのだから,のところにどんな値を入れてもいい.もちろん z-i を入れてもいいのだから,次のようにできる. 結局はというわけだ.色んな関数のテイラー展開の式とその収束する範囲を知っていれば,ローラン展開の役に立つだろう.

具体例（その7）

ついでにもうひとつ. これは前回,「真性特異点」を持つ例として出てきた関数だ. z=0 がその真性特異点になっている.

これも先ほどと同じように指数関数 e^z のテイラー展開を利用すればいい.先ほどのテイラー展開の式のの代わりに 1/z を代入してやればいいのである. このように主要部の項が無限に続くというのが,真性特異点の周りでローラン展開した時の特徴である.このことについても次回,もう一度まとめることにしよう.