物理数学：一次変換

基本的な一次変換の表現

一次式の使い道は連立方程式を解くばかりではない.次のようなことも表現できる. 見ての通り,変数 (x,y,z) の値を決めると,それに応じて (x',y',z') の値が決まるというのだ.これは 3 次元空間中の点 (x,y,z) から別の点への移動,あるいは 2 点の対応関係を表しているというイメージで見ることもできる.こういうのを「一次変換」あるいは「線形変換」と呼ぶ.

それにしても・・・.これは連立一次方程式と形が非常に似ているではないか！まぁどちらも一次式だという縛りの中でやっているのだから当たり前と言えば当たり前か・・・.今何を考えたかと言うと,この式を前のように係数だけ抜き出して略して表示できるのではないかということだ.次のように書けるだろう. 今回は (x,y,z) を省略してしまわないで残しておいた.それは今までとは目的が違うからだ.行列内の係数を使って (x,y,z) を変換することで (x',y',z') になるというニュアンスを残す必要があった. (x,y,z) を縦に表示しているのは,これが左辺にあると対等な存在であることを表現したものである.

しかし毎回このような行列を書くのは面倒なことがある.さらなる略表現を工夫しよう.係数の詰まった行列部分を大文字のアルファベットで表し,ベクトル (x,y,z) の部分をいかにもベクトルだという感じに太字でとでも書こう. これらの略記法を使えば, のように楽に書けて説明に便利だ.今後は時と場合に応じてこのような表現を使って行くことにしよう.

行列の積の導入

先ほどは行列によって点が点へと移動させられる様子を表現した.そのが別の行列によって,今度はさらなる別の地点 x'' へと移動したとする.例えばこんな感じ. 略記法を使えばこうだ. この (3) 式の (x',y',z') の部分に先ほどの (2) 式の右辺を丸ごと代入できそうだ.すると,次のように書けるだろう. これは (x,y,z) から (x'',y'',z'') へと変換する式だと言える.略記法を使えばこういう感じだ. このの部分にはから x'' へ至る道筋のデータが詰め込まれている.さて,これを一つの行列にして表現することは可能だろうか？つまり地点を経由しないで直接 x'' へ向かうのような変換を実現してみたいのだ.それは可能だ.そこで,結果がという行列になるような,行列と行列の積を定義してやることにする. この具体的な計算方法は,読者に強い興味と暇があれば自力で導き出すことだって出来るだろう.しかし今は先を急ぐので,今から結果だけ書いてしまうことにする.答えを先にばらすようなこの話の進め方にちょっと罪悪感がないでもないが,意味も説明しないままにいきなり「行列の積とはこういうものだ」と計算手順を示すところから入る教科書だって多くあるのだから,責められるほどのことでもないはずだ.

行列の積の計算手順

行列の積の計算手順は,理屈で覚えるよりも形で覚えた方が早い.

まず,最初の行列の 1 行目と,後ろの行列の 1 列目を取り出す.

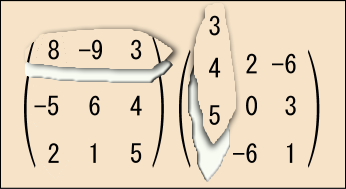
そして,これらの 1 番目どうし,2 番目どうし,3 番目どうしを掛け合わせて,全部足す.ここの例では次の計算をすればいい. これが行列の (1,1) 成分の値になる.次は,最初の行列の 1 行目,つまりさっきと同じものと,後ろの行列の今度は 2 列目を取り出して同じことをする.その結果が行列の (1,2) 成分の値になる.同じ調子で,今度は後ろの行列の 3 列目を取り出して計算して (1,3) 成分の出来上がり.そこまで行ったら,最初の行列の 2 行目を使って (2,1) 成分, (2,2) 成分, (2,3) 成分.こんな具合にして,9 個の成分の値を一つ一つ,ちまちまと求めていくわけだ.

ここでやった計算手順は式を使ってシンプルに表すこともできる. 説明が必要だろうか？念のため書いておこう. $c_{ij}$ というのは行列の (i,j) 成分.それを計算するためには,行列の (i,k) 成分と行列の (k,j) 成分を,の値を変えながら足し合わせて行くという意味だ.今やったのとまったく変わらない.

交換法則について

ところで早めに注意しておいた方が良いことが幾つかある.その一つは,行列の積の順序に関することだ.

今計算したのはという順序で計算した積である.これをもしという順序にして計算すると,まったく違った結果になるだろう.行列の積では $\color{red}{AB=BA}$ という関係が成り立っていないのである.

これは意味を考えれば当たり前だとも言えるだろう.点をまずを使ってどこかへ飛ばし,その飛んで行った先の地点をを使ってさらに飛ばすことをするのがだ.しかしを計算すれば,それは点をまずを使ってさっきとは違うどこかへ飛ばし,それをを使ってまたどこかへ飛ばしたことになるわけだ.これらが同じ地点にたどり着く保障なんてまるでないのがイメージできるだろう.

数学用語を使えば「行列の積では交換法則が成り立っていない」と表現できる.

しかし場合によってはたまたま AB=BA となる状況もないではない.条件を絞れば,たまたまでなく常に AB=BA となったりする状況も作り出せる.例えば対角行列どうしの積の場合には順序を交換しても同じになることがすぐに確認できるだろう.他にもそういう例があるが,あとで話すことにする.

形の異なる行列の積

注意点はまだ幾つかある.行列の積は正方行列どうしの間だけに定められるものではない.例えば次のような式を見て欲しい. これは 3 次元中の点 (x,y,z) を 2 次元平面上の点 (x',y') へと対応させる変換である.これも線形変換の一種である.この場合の変換行列は 2×3 の行列として表されるであろう.

この平面上の点 (x',y') をさらに次のような式で 4 次元空間内の点 (w'',x'',y'',z'') に飛ばすこともできる. この場合の変換行列は 2×4 である.これらの行列を使って,次のような積を考えることができるだろう. 先ほど説明したのと同じ方法で計算できるはずだ.これは 3 次元上の点を 2 次元を経由して 4 次元上の点に飛ばすと言う意味であり,計算結果は 4×3 の行列となる.これは 3 次元上の点を直接 4 次元上へ飛ばす行列になっている.

しかしこれらの行列を次のように逆にして計算することは出来ない. この場合には先ほど説明した計算方法を当てはめることが出来ないことが分かるだろう. m×n の行列と p×q の行列があるとき,の計算をするためには n=p になっていなければ実行不可能なのである.こういう意味でも AB=BA は常に成り立たないというわけだ.

ところで,(2) 式の右辺を見てもらいたい.これは 3×3 の行列と 3×1 の行列の積だと考えることができる.(1) 式の右辺はこれと同じ意味だが,先ほど説明した積のルールにちゃんと従っているのが分かるだろう.例外なく同じルールが支配しているのを見るのは気持ちがいいものだ.

結合法則について

ABC という,行列の積が連続する状況があるとする.これは点をまず行列で変換し,変換した先の点を次に行列で変換し,さらにで変換するというイメージである.この行列を計算するとき,先にを計算してもから先に計算しても結果として行き着く先は変わらないはずである.つまり,次のことが成り立っている. これは数学用語を使えば「行列の積においては結合法則が成り立つ」と表現できる.

これは三つの行列の積に限った話ではない.幾つもの積が並んでいる状況であっても,どこから計算してもいいというわけだ.

加算について

行列の関係を等式で表すようになったからには,それを移項した表現に直したりすることもあるだろう.そこで,行列どうしの和や差についても定義しておく必要がある.しかし大して難しいルールではない.

行列の足し算や引き算は,同じ型,つまり行と列の数が一致する行列どうしの間でのみ成立すると決めておこう.計算方法は,同じ位置にある要素どうしを足したり引いたりするだけだ.

わざわざ書くことでもないが,一応書いておこう.行列の加算では交換法則が成り立つ. A+B=B+A が成り立つということだ.

そうそう,結合法則も成り立っている.これは (A+B)+C=A+(B+C) だということだ.

零行列

行列内の要素が全て 0 であるような行列を「零行列」（ぜろぎょうれつ・れいぎょうれつ）と呼び,アルファベットのオーの大文字を使って表す.私の場合,を使わずに数字の 0 を使うかもしれないが,あまり気にしないで文脈から正しい意味を読み取ってもらいたい.

すぐに分かってもらえることだと思うが,行列の積の計算の中に一つでもこれが入っていると,結果は必ず零行列になる.他の行列に零行列を加えても,何の変化もない.これは普通の数字の 0 に良く似た性質のある行列だ.

単位行列

さて,ここまでは行列の型に関係なく通用する話だったが,これからしばらくは正方行列に限った話をしようと思う.次元の異なる空間へと点を飛ばすことには今のところは興味がないからだ.あとでそのようなことも論じるかも知れないが,それはずっと後になるだろう.

さて,点を元の位置からまったく移動させない線形変換がある.行列で書けば,例えば次のようなものだ. これらを「単位行列」と呼ぶ.これを表す記号はやが良く使われる.はドイツ語の Einheitsmatrix,は英語の Identity matrix がその起源だと言われている.どちらも単位行列という意味だ.

私はどちらの記号を使おうか.考えてみると,頭の中が数学モードの時はを使い,物理モードの時はを使っている気がする.多分,過去に受けた授業の影響だろう.この数学の記事中ではを使うことにしよう.

単位行列は,どのような行列との積を計算しても,もとの行列を変化させることはない.次のようである. 意味を考えれば当たり前だな.単位行列は,行列の積においては,まるで数字の 1 のような性質を持っていると言える.

逆行列

正方行列どうしの積を計算した結果として,次のようになることがある. 行列とで立て続けに移動した結果を一つの行列で表すと,単位行列になるというのだ.これは結局は何も動かさなかったのと同じ.つまり,行列でどこかに移動して,別の行列によって元の位置に戻ってきたという意味だ.

互いに掛け合わせた結果が 1 になるというイメージなので,逆数に似た性質だと言えるだろう.そこで,このような行列のことを「 $\color{red}{A}$ の逆行列」と呼び, $A^{-1}$ という記号で表す.

この記号を使って先ほどの式を書き直すと,つまりはこういうことだな. ところが不思議なことに,逆行列には次のような関係も成り立つという性質がある. 積の順序を交換しても結果が変わらないだと！？なぜこんなことになるのか,イメージできるだろうか？もしの逆行列がだとすると,の逆行列はだというのだ.

イメージを再確認しておこう.行列で点がどこかへ移動したとすると,それがもとの点に戻るための行列は一つきりに違いない.つまり行列が定まれば,行列,すなわち $A^{-1}$ はきっと一つだけ存在するわけだ.

いや,実はそうとは言い切れない場合がある.例えば行列によって 3 次元上の点が,3 次元内に存在する,ある一つの平面の上や,ある一つの直線の上に集中してしまう場合だ.一度こうなると,それぞれがどこから来た点であるかが区別できなくなって,どう頑張ってももとの 3 次元内の位置に戻しようがないのである.つまりこういう場合には逆行列を持たないわけだ.そういう,ちょっと悪い癖のある行列についてはあとでゆっくり考えることにしよう.

とにかく普通の行列ならば,逆行列を一つきりだが持つはずである.そこで,逆行列を持つ普通の行列のことを「正則な行列」と呼ぶことにしておこう.

今不思議なのは,最初に逆行列 $A^{-1}$ を使ってをどこかに移動させておいても,それをを使ってもとの場所に戻すことが可能だというのである.と $A^{-1}$ とはまったく別の中身を持った行列であるのにだ！

不思議なことではあるが,そうでなくてはならない証明なら簡単にできる.今,の逆行列をとしよう.そして,にも逆行列があるが,それはだとは認めたくないのでとでも表しておこう.つまり,次のような関係が成り立っている. このとき, CBA という 3 つの行列の積を計算してみよう.計算手順の違いによって次の二通りの結果が得られるはずだ. どちらも同じもののはずなので, C=A であることを結論しなくてはならない.どうだい,これ！？

まとめと次回予告

一次変換を行列で表せること.一次変換の繰り返しを行列の積で表せること.その計算の定義を学んだ.

興味深いのは逆行列の存在だ.逆行列の具体的な形は計算で求めることができる.次回はその話でもしてみようか.