固有ベクトルとは? 固有値とは?
線形変換によって位置ベクトルの方向や長さが変化するという図形的イメージを学んだ.
ところが,ちょっと変わったものもあって,線形変換の前後で方向の変らないベクトルというのが存在することがある.それを「固有ベクトル」と呼ぶ.方向が変わらないことが大事であって長さは変化してもいい.固有ベクトルの長さが変換の前後で何倍に変わったのかを表す倍率のことを「固有値」と呼ぶ.用語の意味としてはたったそれだけのことだ.
今回はその固有ベクトルと固有値の求め方について説明する.こんなものが何の役に立つのかについては次回まで明らかにならないだろう.あまり先走った疑問を抱えて疲れないようにしてほしい.
本当は固有ベクトルが何の役に立つのかの方から先に説明しようとしたのだが,そのためには固有ベクトルと固有値の性質を少しは知っていないと話が進まない.予め少しだけ話しておくというのも中途半端な気がするので,いっそのこと,一通りをここでまとめて説明してしまうことにした.
固有ベクトルのある場合、ない場合
変換の前後で方向の変らないベクトル!三つ前の回で学んだイメージを再び思い出そう.
例えばもともとだったものが線形変換によって反時計回りに傾き,
だったものが時計回りに傾いてくる.そんな 2 次元での変換を想像してみよう.間に挟まれたベクトルはそれらに合わせるようにして,あるものは時計回りに,あるものは反時計回りに位置を詰めてくる.その中間のどこかに必ず,向きを変えないベクトルが存在するはずだ.

そういうベクトルは一つきりじゃない.それと同じ方向を向いた,長さの違う無数のベクトルが当てはまる.しかし元から長いベクトルはそれだけ遠くへと変換されるのであり,長さの変化の倍率はどれも同じ.つまり固有値はどれも同じだ.逆方向を向いているベクトルも固有ベクトルである.

固有ベクトルは一つの方向だけだろうか.いや,と
とが間を詰めた分だけ,別のところでは広がった領域もあるだろう.広がっていくその領域の中間のどこかにもう一つ,固有ベクトルの一群が存在する方向があるはずだ.その固有値は先ほどとは違っていてもいい.いや,違っている事の方が多いかも知れない.次の図では変換後のベクトル(赤)の方が変換前(黒)よりも短くなっており,固有値は 1 より小さいのだろう.

しかしこんなのは一例に過ぎない.
と
とがどちらも同じ向きに回転するように動いたとしたらどうだろう.少しばかりひしゃげながらも平面全体が同じ方向へ向かって回転する.そのような状況で向きの変わらないでいられるベクトルなんて存在するだろうか?無いような気がする.いかにもそんな気がするだろう?このように,固有ベクトルは存在しない場合もある.
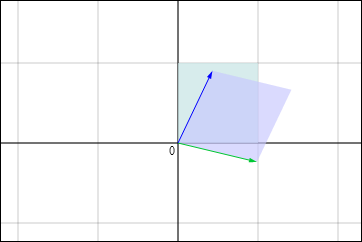
しかし実はこのような状況であっても固有ベクトルが存在することもあるのである.例えば,次のような具合に.赤い線が固有ベクトルの方向を表している.
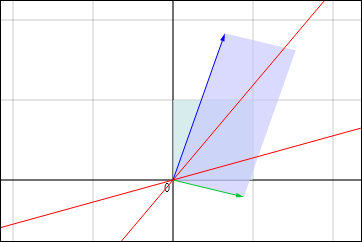
このように,直感を裏切るようなことがたびたび起きる.しかし変換前後の平行四辺形の形を見て,どの点がどこに対応するかを考えれば,なぜそうなるのか分かるはずだ.
これら以外にも意外な方向が固有ベクトルになる状況が起こり得る.固有値は負の値でも構わないのである.変換前後で向きが逆転してもいいわけだ.こういうのは変換後にと
の位置が入れ替わるか,それに近い状況で起こるだろう.詳しく考えることは読者に任せることにする.
以上の話は固有ベクトルというものをより具体的にイメージしてもらいたくて書いたものである.あらゆる状況を言い尽くしてはいない.こういうことをあまり深く考えなくとも,これ以降の話を理解するのには支障はないと思う.しかしあれこれと考えてみるのは良いことだ.
あ,そら見ろ,まだあるぞ.と
とが変換後にどちらも同じ直線上に乗る場合なんてのはどうか.平行四辺形がひしゃげて完全に潰れてしまう状況だ.元からその直線上にあったベクトルだけが固有ベクトルであろう.
他にはと
のどちらか一つの向きだけが変化する場合.動かなかった方の軸上にあるベクトルが固有ベクトルであり,それ以外のベクトルはすべて向きを変えるのではなかろうか.この場合には固有ベクトルは一つの方向だけとなるだろう.いや,最初はそう思ったのだが,実際に試してみると必ずしもそうなるとは限らないようだ.
うーん,ひょっとして今ので言い尽くしてしまったかな?いやいや,まだまだあるな,大丈夫.
試してみよう
ここまでに書いたことを手軽に確かめることができるように,今回もウェブアプリを用意してみた.申し訳ないが,今回も HTML5 対応のブラウザでしか使うことができないし,まだスマートフォンにも対応していない.対応ブラウザは世の中にいくらでもあるから不便はそれほどはないだろう.
固有値と固有ベクトルの求め方
では次に,これらの固有ベクトルを計算で求める方法を説明しよう.固有ベクトルをで表す.これを行列
で変換すると
となる.変換した結果,元の
を定数倍したものになるというのだから,その状況を素直に式で表すと次のようになるだろう.
ここに使った定数
というのが固有値のことである.この式の右辺を移項してやると,次のようになる.
ここで出てきた
というのは単位ベクトルで,これを掛けても何も変化しないのだった.行列
と形式を合わせて括弧でくくるために導入したのである.
さて,この式に表された条件を満たすようなとはどんなものだろうか?
というのはその一つではあるが,まるで面白くない答だ.ゼロベクトルは固有ベクトルとは呼ばない.それ以外の解に興味がある.
ここからは具体的な例を使って計算した方が分かり易いだろう.行列を次のようにしてみよう.
今からこのような 2 次の行列
の固有ベクトル
を求めるのである.さて,この行列
の具体的な数値を使うと,(1) 式の
の部分は次のように書ける.
要するに,次のような式を満たす
が欲しいわけだ.
の値がまだ不明ではあるが,この (2) 式は形としては
と
についての連立方程式である.連立方程式が唯一の確定した解を持つ条件というのは「行列式が 0 でないこと」だった.さっきも言ったように,ここでの唯一の明らかな解というのは
かつ
というものだが,それはつまらな過ぎるので欲しくないのだ.だとすれば,行列式が 0 になるように仕向けてやればいいではないか!
こうなるように
の値を決めてやるのだ.この条件式 (3) には「固有方程式」という呼び名がついている.今回の場合には 2 次方程式だから解は二つ出てくる.
こうして固有値が求められた.
それぞれの値について,これから同じような計算を繰り返すことにしよう.まずは (2) 式にを代入してやる.
行列の中の二つの行が,一方を定数倍したら他方と同じになるというような関係になった.行列式が 0 になるようにしたのでこういうことが起こるのは当然なわけだ.結局のところ,この式の意味するところはこうだ.
この関係を満たすような
と
を用意してやればいい.シンプルなものを選ぶなら例えば
というのがその一つだ.これを定数倍したものもみんな当てはまる.マイナスを掛けてもいい.ただ,0 を掛けてしまうと特徴がなくなってしまうので除外しておこう.ゼロベクトルは固有ベクトルではないのだ.ベクトルの長さが 1 になるように調整して,
のように表すこともあるが,そうしなければならないということもない.これを定数倍したもの全てが求めようとしていた固有ベクトルであり,「固有値 5 に属する固有ベクトル」という呼び方をする.
固有値はもう一つあるのだった.次にを (2) 式に代入して同じことをしてみよう.
これは
を意味しており,これを満たすベクトルのうちでシンプルなものを挙げれば
である.これを定数倍したものもすべて「固有値 2 に属する固有ベクトル」である.目立つように(つまり,説明の構造が視覚的にも分かりやすいように配慮して)ベクトルの長さを 1 に調整してやったものを書いておこう.
繰り返すが,ベクトルの長さを 1 に調整しておくなんてことは全く本質ではないのだ.ただ私が,見た目がすっきりしているという理由だけで多数の固有ベクトルの中から一つのベクトルだけを選んで書くことにどうにも納得できなかったから,せめて長さが 1 だという特徴のあるベクトルを代表として選んでみただけのことである.
固有値の数
ここまでの手順が理解できたら,細かいことはもう読者に任せて大丈夫だろう.たとえ行列の次数が増えても考え方は上で説明したものと何も変わらない.ただ計算の手間が少しばかり増えるだけである.
・・・と言って話を終わらすことが出来たならどんなに良かっただろうか.
確かに手順自体は今説明した通りなのだが,実際に色々な行列について計算してみると予想外の事態に遭遇することがある.その対処法もちゃんと話しておかないといけない.
例えば 3 次の行列になれば,固有方程式は 3 次方程式になる.そうなると固有値は 3 つになるだろう.だからそれぞれについて 3 通りの固有ベクトルを求めてやらないといけない.いや,そんなに単純ではないな.固有値は必ず 3 つあるとは限らない.重解になる場合があるからだ.
それを言ったら 2 次の行列でも重解になる場合が出てくる.それどころか,実数解を持たないことさえあるだろう.
補足:2 次方程式は実数解を持たないことがあるが,3 次方程式は必ず一つは実数解を持つと言える.それはグラフを思い描けば理解できるだろう.奇数次の曲線は x 軸との交点を必ず持つが,偶数次の曲線は交点を持たない場合があるからである.
実数解がない場合には固有値は一つも存在しないし,対応する固有ベクトルも存在しないと考えて良い.そういうことも起こり得るのだ.
予告:ただし,しばらく後で行列やベクトルの成分を複素数に拡張するという思い切ったことをするつもりでいる.その時には固有値が複素数であるという事態も許されることになるし,それに属する固有ベクトルも複素数で表される.つまり,固有ベクトルはいつでもちゃんと存在するということになるわけだ.しかしそうなるともう図形的にイメージすることが非常に困難になるので,抽象的な論理として割りきって受け入れるしかないだろう.だからそういう話は一通りの話を終わったあとでやるつもりである.
固有ベクトルが決まらない?
その他には何か特別な事が起こり得るだろうか?あ,そうだ.あらゆるベクトルが固有ベクトルになるという事態があり得る.それはを計算したときに全ての成分が 0 になるような場合である.
そうなるとどんなベクトルでも条件が成り立ってしまうのである.それが起こるのは
が単位行列だったり,その定数倍だったり,そういうものに似た形だったりという極めて限られた場合だけであろう.
今回用意したウェブアプリでそういう状況も作り出せるので色々と試してみてほしい.というか,アプリを開いた直後の状態がまさにそのような状況の中の一つになっている.
こういう時には,例えば 2 次の場合には,線形独立な二つのベクトルを何でもいいから
のように勝手に選んでやって,これらが固有値〇〇に属する二つの固有ベクトルです,と答えておけばいい.こんな風に,同じ固有値に属する線形独立な固有ベクトルが複数あるということがあるのである.固有値が
重解の場合にはその固有値に属する固有ベクトルが最大で
個まで存在するのだが,それ以下の場合もある.それについての詳しい話はいつか機会があればということにしておこう.
あらゆるベクトルに固有ベクトルの資格があるはずなのに,なぜこんな風に代表となるような固有ベクトルをわざわざ勝手に選ぶのかと不思議に思うかも知れない.実は,そういう考え方をしておいた方が次の話にスムーズにつながるからである.答は次回までおあずけである.ここでは最もシンプルな選び方をしたが,都合に応じて他の選び方をしてやってもいい.線形独立ならどんな二つのベクトルを代表に選んでやってもいいだろう.
楽するためのヒント
その他に言っておいた方がいいこと・・・.うーん,考えてみたらまだ色々とあるものだなぁ.勘の良い人なら自分で対処できるかも知れないけれど,つまづく人も多いと思うのだ.仕方ない.思い付いたものから一つずつ潰していこう.
上でやった例では 2 次だったから固有方程式を作るのは簡単だった.しかし 3 次以上になると,行列式の公式に従ってかなり複雑な計算をしなくてはならなくなる.・・・って,そんな効率の悪いことをしてちゃいけないよ!?
すでに行列式の値を変えないで行列を変形する方法は話したし,上三角行列を作る方法も説明済みである.そこまでやれば対角成分の積を計算してイコールゼロと置くだけで固有方程式が出来てくるはずではないか.
とは言ったものの・・・.うーん,が混じってるものを上三角行列に変形するのはやっぱり大変だ.ちょっと試してみたが,3 次くらいではまだ普通にサラスの公式で計算した方が楽だと思う.4 次以上を計算することになったらそういうやり方もあるということを思い出してみてほしい.
教科書の例題や演習問題というのは,簡単に計算できたり,結果が綺麗な整数値として出てくるように色々と細工がしてあるものである.載ってる解法もかなりエレガントに見えるが,それはページ数の都合に違いない.私が自分で適当に作った問題で試してみたら,めちゃくちゃ面倒な計算を強いられたし,結果も複雑だった.どうやらいつでも簡単に計算に応用できるような便利なテクニックというものはなさそうだ.安心して迷わず地道に計算してほしい.まぁ,やり方さえ知ってれば,そういう作業はコンピュータにやらせりゃいいんだよ.
次数が増えたとき、困惑しないために
先ほどの 2 次の行列を使った計算例は,分かりやすいという利点はあるのだが,逆に簡単すぎるという弱点もある.同様のことを 3 次の行列で試してみるだけで,先ほどとは変わった状況が出てきてしまうのである.
例えば先ほど,行列に固有値
の具体的な値を代入したときに,
のように 1 行目と 2 行目が互いに定数倍であるという関係になっていた.ところが 3 次以上の場合にはこんなに分かりやすいことにはならないのが普通だ.
次の行列を使うというのは
個の連立方程式を考えているのと同じである.ところがこれらの式が全て独立になっていると一つに定まった解を持ってしまう.今は一つに定まった解というのはゼロベクトルのことであって,それは面白くないので避けたい.それで行列式が 0 となる条件を考えて,それらの式を独立ではなくしてしまったわけだ.要するに,得られた固有値
を代入した後では,行列のランクが
より小さくなっているということである.
2 次の場合には 2 より小さなランクは 1 か 0 しかないので,先ほどのような簡単な説明だけで起こり得る状況をほとんど言い尽くせてしまったのである.というわけで,3 次以上の場合に起こる事についても少し補足しておいた方がいいと考えている.
説明する側にとって都合の良すぎる例を持ち出してみよう.例えば,計算していて次のようになったとする.
これは 3 つの式の連立一次方程式を表しているが,それぞれの式はすでに独立ではないはずだ.(そうなるように
を定めて代入した結果がこれなので.)ランクが 3 以外,つまり 2 か 1 だろう.0 ではないのは一目で分かる.もしランクが 0 なら行列内の全てが 0 のはずだからだ.ガウスの消去法によって上三角行列を作るように変形すればはっきりする.
独立な式は二つしかない.つまりランクは 2 だったわけだ.この式の意味するところはこうである.
これらの式を満たす
はどういうものだろうか.「解は不定」で終わらせずに詳しく考えてみよう.条件が一つ足りないのだから,不定値一つ分の自由度があるはずだ.とりあえず
とでも置いてやることにしよう.すると 2 番目の式から
であり,これを最初の式に代入して
であることも出てくる.まとめて書けばこうだ.
は任意の実数であることだし,なるべくすっきりするように調整すれば,固有ベクトルの代表を次のように書いてもいいだろう.
先ほどはベクトルの長さを 1 に揃えるための係数をこだわって付けていたわけだが今回は面倒くさくなったのでやめておこう.所詮その程度のこだわりだったということも知っていてもらいたい.
次は 3 次の行列を使った時に起こり得る他の例,ランクが 1 の場合をやってみよう.例えば計算していって次のようになったとする.
よく見ると,各行が互いに定数倍という関係になっている.それに気付けばもうわざわざ掃き出し法を使う必要はないのだろうが,気付かないこともあるだろうから,いずれにしても掃き出し法を使ってやればいい.次のようになるはずだ.
確かにランクは 1 だ.そしてこれは
であることを表している.これは解を確定させるための条件式が二つ足りないわけだから,二つ分の自由度があるはずだ.その自由度を表す二つの変数
,
を用意して,
,
とでも置けばいい.すると
となるだろう.結果をまとめて書けばこうだろうか.
これをどう解釈すべきかが問題である.
と
は任意の実数なのだから,平面の自由度がある.上の式に見えている二つのベクトル
と
とを含む平面内に乗っているようなベクトルならどれでも,固有ベクトルとして相応しいのである.
そんな中からどれかを選べと言われても困ってしまうが,ここではその平面内から,線形独立な二つのベクトルを,好みと都合に応じて選ぶことにしよう.
こういうことは先ほど 2 次の場合にもやっただろう.同じ固有値に属するベクトルが二種類あると考えておけばいいわけだ.
これと似たような状況がもう少し分かり易く現れる例をもう一つ見ておこう.計算していって,掃き出し法も使った後の結果として例えば次のようになったとする.
ここから分かるのは
つまり
であることが確定だということだ.ただし
と
が不定である.要するに
平面内のベクトルならどれでもいいわけだ.その中から独立な二つのベクトルを選べと言われたら,普通は次のような無難なものを選ぶところだ.
しかしもちろん,
みたいな妙ちくりんな組み合わせを選んだとしても間違いとは言い切れない.
さあ,これだけ紹介しておけば,未知の事例に遭遇したときにも困惑することはなくなるだろう.同じような考えで乗り切ればいいわけだ.
舞台裏
え?ここまでに例として挙げた色んな状況がどういう行列を使ったときに発生するかって?そういう良い疑問が生じたなら自分で確かめてみるといいだろう.私は説明に都合のいい,かつ美しい具体例を見出そうとして散々苦労した.その苦労の一部でも分かち合おうではないか.
ヒント:苦労したとは言っても,気付いてしまえば実はくたびれ儲けだったかも知れないと思える.逆の方向から考えればとっても簡単な話に過ぎなかったのだ.まずはランクを落とした上三角行列を都合のいいように好き勝手に作ってやって,基本変形を使って元の形を適当に隠し,普通の行列のように見せかける.それから勝手に決めた固有値を対角成分に足してやれば,望み通りの結果をもたらす例が作れるというわけだ.ああ,もちろん,完全に無駄な苦労だったとは思っていない.ここに書いてない色んなことを自力で発見できた.
今回の話の目的は固有値,固有ベクトルを求める方法が分かることなので,それ以上の内容に踏み込むつもりはない.数学書には載っているような様々な定理の紹介もまだしない.固有ベクトルを何に使うのかも分からない内からそんな事にまで興味が湧かないという人も多いことだろう.
修正履歴
(2025/08/21)
・誤植の修正.「次数が増えたとき,困惑しないために」のところの3次の行列の右下の値 (誤)2 → (正)-2










