論理ゲートの話
前回の話で出て来た「量子ゲート」というのは,古典的コンピュータが「論理ゲート」と呼ばれる要素を組み合わせることで実現されていることにイメージを重ねたネーミングである.
量子コンピュータと古典的コンピュータの仕組みは似ている部分があるので,少し古典的コンピュータの仕組みについての説明に寄り道してみよう.古典的コンピュータでは 1 か 0 かがはっきり定まっている状態を利用している.これを普通は「ビット」と呼ぶのだが,ここでは「量子ビット」と話が混じらないように「古典ビット」と呼ぶことにする.
論理ゲートというのは古典ビットの入力に対して,古典ビットを出力してくるユニットである.例えば ANDゲート,ORゲート,NOTゲートなどがある.一つの論理ゲートを構成するのに数個から十個程度のトランジスタを組み合わせて回路を組む必要があるが,一つの IC の中に数個の論理ゲートが封入されたものが売っているので今となっては自分でゲート自体を設計する必要はない.論理回路の設計者は,論理ゲートの組み合わせを作ることだけに集中すればいいのである.
論理ゲートの幾つかを紹介しておこう.NOTゲートというのは 1 つの古典ビットの入力に対して 1 つの古典ビットを返すゲートである.1 を入れると 0 が出てきて,0 を入れると 1 が出てくる.要するに,古典ビットが反転して出てくるのである.
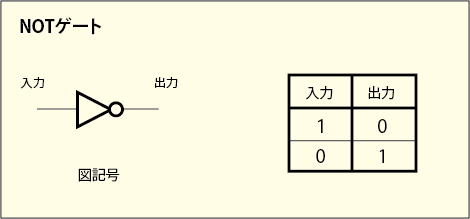
電源は別のところから供給されているので図記号では省略されている.このようなブラックボックス化は実際の回路の複雑さに煩わされることがないので便利である.他のゲートも同様である.
ANDゲートというのは 2 つの古典ビットの入力の組み合わせに対して 1 つの古典ビットを返すゲートである.入力の両方が 1 であるときに限って 1 を返し,それ以外は 0 を返してくる.
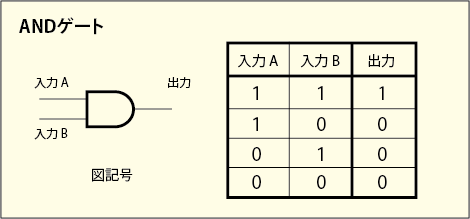
ORゲートというのは ANDゲートと同じで,2 つの古典ビットの入力の組み合わせに対して 1 つの古典ビットを返すゲートである.入力のどちらか片方でも 1 であるなら 1 を返してくる.
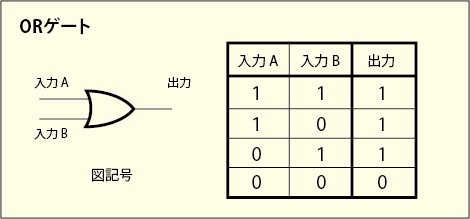
論理ゲートには他にも種類があるのだが,この 3 つがあれば十分である.なぜならこの 3 つはブール代数における「否定」「論理積」「論理和」に対応しており,あらゆる古典的な論理はこの 3 つのルールに分解して表せることが分かっているからである.
これらのゲートを組み合わせることで,2 進数で表された数値の足し算などの機能が実現できるのである.多数の古典ビットを並べてそれを 2 進数で表された数値と見なし,それぞれの数値の古典ビットの状態の組み合わせを見て,どんな値を出力すれば足し算を実行したことになるかを考えて論理回路を組む.例えば 2 進数の 1 桁どうしの足し算は次のような論理回路を組めば実現できる.
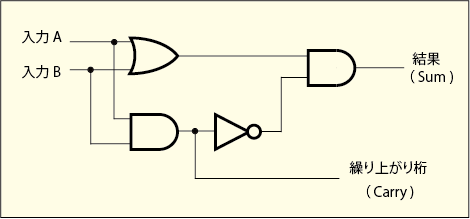
2 桁どうしの 2 進数の足し算は下の桁からの繰り上がりがあるかどうかを判断基準に入れる必要があるので,今見たような論理回路を使ってから,再度,繰り上がりを加えるための回路を通せばいい.同じような回路を二つも書くと複雑なので,上の回路を次のようにブラックボックス化してみよう.
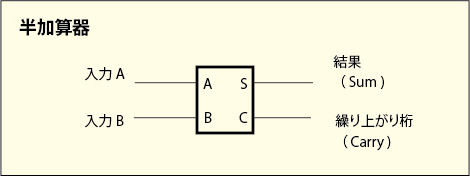
これを二つ使えば繰り上がりを考慮した回路の動作も簡単に理解できる.

これは「全加算器」と呼ばれている.これだけ色んなゲートを組み合わせても 1 桁分の計算が出来るだけである.しかしこれがあればあとは簡単だ.桁数が増えてもこれと同じものを桁数分だけ並べてやるだけでいい.8 ビットのコンピュータならこの「全加算器」を 8 個並べてやることになるだろう.実はこのような論理回路をいちいち設計しなくても,一つの IC に幾つかの全加算器を封入したものが売られている.
古典的コンピュータが行う計算というのはこのように機械的な仕組みで実行させている.数値を 2 進数で表して,それを電圧で表して,論理回路に入れてやれば,しばらくは桁の繰り上がりなどで結果が変動するだろうが,遅くとも数マイクロ秒後には状態が落ち着き,正しい計算結果が得られるというわけである.
例えばクロック周波数が 1 MHz 程度のコンピュータなら約 1 μ 秒後より以前に結果が安定していればいいのである.現在のコンピュータはトランジスタの電子の移動度も高くてもっと速いし,それ以外にも早く安定した答えにたどり着くための様々な工夫がしてある.要するに,繰り上がりの結果が下の桁から順に上がってきて結果がなかなか安定しないのが問題なので,そこに論理的な近道を作ってやればいい.例えば,上半分の桁と下半分の桁を分けてやってそれぞれを独立して計算させてやる.上半分の桁については繰り上がりがある場合とない場合を計算する二通りの回路を用意しておいて,それぞれの計算結果を得る作業を先に同時に済ませておく.あとで下半分からの繰り上がりを見てから,それに応じてどちらかの計算結果を採用するという論理回路も組めるだろう.回路はかなり複雑になるが,すばやく安定する.8 ビットならともかく,最近の 32 ビットや 64 ビットのコンピュータではそのような方法で高速化しておかないとつらいだろう.
引き算の回路は意外と簡単である.2 進数で負の数を表す方法を知れば足し算と同じ回路で計算ができる.「2の補数表現」というものだ.これを作るのは簡単で,全部のビットを反転させて 1 を加えるだけでいい.つまり引こうと思っている数値の信号を全て NOTゲートを通してから普通に足し算の回路に通して,さらに 1 を加えるという方法でいい.一番下の桁にも全加算器を使っていれば,その使っていない下の桁からの繰り上がりの信号線を利用して 1 を加える回路ができるだろう.
セレクタ回路
論理回路で実現できるのは足し算や引き算だけではない.古典ビットを並べて 2 進数とみなしたとき,その 2 進数が表す数値がだったとすると,
番目の線だけに電気を流すという仕組みも作れる.これは「セレクタ」あるいは「マルチプレクサ」などと呼ばれている.
例えば 3 つの線を使って数値を表現してみる.その場合,0 ~ 7 の合計 8 つの 2 進数を表せることになる.この数値に応じて 8 つの線のうちの一つだけに電圧がかかるようにしたい.それは次のような回路で実現できる.
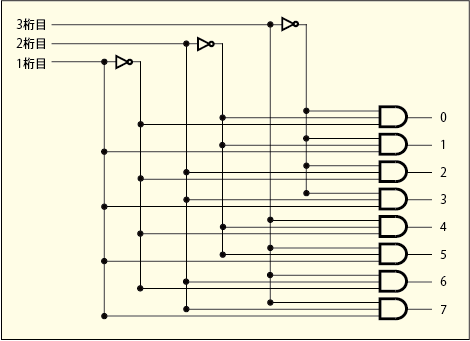
普通の回路図の約束とは違って配線の曲がり角にも黒丸が付けてあるが,これはどういう規則で配線をしているかを分かりやすくするためである.
どういう考えで組まれているかを知るために左上の「3桁目」というところから見ていこう.2 進数で 3 桁目が 1 ならばその数値は 4 ~ 7 のいずれかである.だからそちらに 1 の信号がそのまま行くようにしてある.もし 3 桁目が 0 ならば,その数値は 0 ~ 3 のいずれかなので,NOTゲートで反転させてそちらに 1 の信号が行くようにしてある.
同様な考えで,2 桁目が 1 になる場合と 0 となる場合とでどんな数値になる可能性があるかを考えて,そこに 1 という信号が行くようにしてある.1 桁目も同様である.
それで結局,右側の 8 本の線のそれぞれには 3 つずつの配線が来ているが,その全てが 1 になったときに限って反応するように ANDゲートを入れてある.この ANDゲートは先ほどの説明とは違って入力が 3 つあるが,その全部が 1 の時に限って出力が 1 となるゲートである.それは普通の 2 入力の ANDゲートを組み合わせても実現できるものだが,図が面倒になるのでやめておいた.
これを利用すれば,古典ビットで組み合わせて作った数値に応じてLEDを光らせたりして,2 進数に慣れない人間にも,電線を流れている信号が意味する数値を読めるようにできる.数字の形に光らせるようにすればなお分かりやすい.実はこのような面倒な配線をひとまとめにしてくれてある IC もちゃんと売られているのである.
デジタル表示の数字の形に光るLEDは「7セグメント」と呼ばれているが,それを光らせるための専用 IC もある.2 進数で表した信号を入れるとそれが意味する数字の形に光らせてくれるわけだ.実はゲートの出力は幾つもの LED を直接光らせるほどの電流を取り出すことは出来ない.そこで,トランジスタ回路をつなげて電源を別に取って光らせたり,内部でそのようなことまで面倒を見てくれている専用 IC を使う必要があるのである.
メモリの原型
さらに,論理ゲートの出力を再び入力側に戻すという反則技のようなことをすれば面白い性質を持つ回路が実現できる.
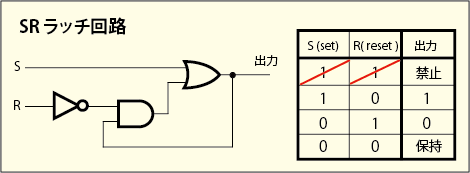
これは「SRラッチ」と呼ばれる回路である.入力が二つあって,S(セット)と R(リセット)を意味している.S = 1 かつ R = 0 にすれば出力は 1 になり,その後に両方を 0 に戻しても出力はそのまま 1 である.S = 0 かつ R = 1 にすれば出力は 0 になり,その後に両方を 0 に戻しても出力はそのまま 0 である.つまり,出力を好きに変化させることができて,なおかつそのままの状態を保たせることも出来るのである.
ちなみに S と R の両方を同時に 1 にするのは無意味である.なぜなら,そこから両方を 0 に戻す過程で必ずどちらかが先にごくわずかだけ早く 0 に戻り,セットかリセットのどちらかを行ったのと同じ状態を経由するからである.どちらになるかは運次第で分からないということだ.
このラッチ回路も IC が売っていて,入力を両方同時に 1 にすることを禁止しているものもある.内部的に同じ機能を持つ独自の回路を構成していて,何かまずいことが起こるのだろう.故障することもあるので説明書には従った方がいい.そういう理由で念のために上の表でも禁止ということにしておいた.しかしこの回路だと出力は 0 になるし,それで問題が起こるわけではない.
このままだと使いにくいというなら,この前段階に次のような論理回路を入れておけばいい.
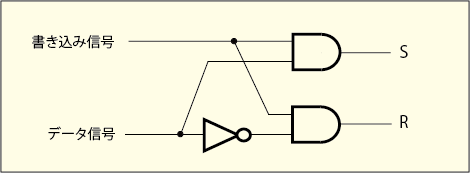
これなら禁止されている状態を入力してしまうことはないし,書き込み信号が 1 になったときに限って,そのときのデータ線の状態をそのまま記憶するという仕組みに出来る.
これはメモリとして使えるだろう.これだけだと 1 ビットしか記録しておけないが,多数並べれば数値を記録しておけるようになる.
メモリを実現するにはこの他にも色々な方式があって,現在のコンピュータはこのような論理回路を組み合わせたものを利用するというよりは,もっと高速に動作する独自の回路を組んでいたりする.書き込み信号もトリガ的なパルスを利用している.それでもここで説明したものはその原型のようなものである.
その他の論理ゲート
上で紹介した 3 種の論理ゲートの他にも幾つかのゲートがある.例えば XOR ゲートや NAND ゲートや NOR ゲートなどというものである.それらは先ほどのゲートの組み合わせでも実現できるのだが,時にはそういうものを利用した方が回路がシンプルになる場合もある.(例えば先ほどの半加算器で繰り上がりの信号線を使わなければ 1 個の XOR ゲートと全く同じものである.)
特に NAND ゲートと呼ばれるものが重要である.
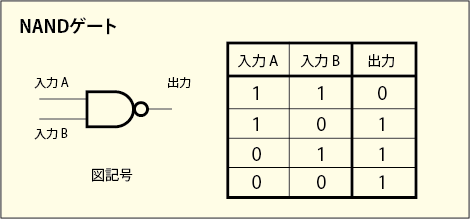
これは AND ゲートの出力側に NOT ゲートを付けたものとして理解できる.NAND ゲートは「万能ゲート」の一つであり,これが 1 種類ありさえすればうまく組み合わせて他の全てのゲートと同じ働きを実現できるのである.しかも NAND ゲートを実現するためのトランジスタ数はかなり少なくて済む.
NOR ゲートというのも万能ゲートなのだが,NAND ゲートの方がIC 内部の回路構造的にごくわずかに楽に作れたり,組み合わせを作りやすいので人気があった.今はそういうことをあまりしないので,それもほとんど過去の話である.
同じ機能を持つ論理回路を作る方法は一通りではなく,手持ちのゲートの種類の都合,回路基板の大きさの都合,配線の都合,予算の都合で,あれこれ調整を行う必要が出てくる.ゲート数を少なく抑えたり,近くの回路と共有できる部分を探したりする.情報学科の学生は「ブール代数」や「カルノー図」などの理論を駆使しながら,その辺りの可能性を自由に取捨選択できるように訓練を受けるのである.
先ほどから「ある程度まとまった機能を封入した IC がすでに用意されている」だとか言っているが,今は論理ゲートを組み合わせて実際の複雑な回路を制作することはほとんどない.そのような IC もあまり使わない.パソコンの上で論理回路を設計して,FPGA というチップに書き込んで使うのである.現在の FPGA は内部に何度でも書き換え可能なメモリを持っており,起動直後にそこに書き込まれた設計のとおりに内部の多数の論理ゲートどうしを接続してから,大規模な論理回路として動く.FPGA は安いものだが,値段によって使えるゲート数も違っており,やはりゲート数を節約する設計の知識は必要になってくる.
古典的コンピュータの発展
古典的コンピュータはここまでに話したところからさらなる大飛躍を遂げている.
例えば,先ほど話したセレクタ回路と 1 ビットのメモリ回路を組み合わせてみよう.たくさんのメモリ回路をずらりと並べてやって,それぞれにセレクタ回路からの線をつないでおく.するとセレクタ回路で指定してやったどれか一つだけのメモリを選んで書き込み信号を送り,そこに情報を書き込むことが出来るようになる.また,全てのメモリ回路から常に出ている何らかの出力とセレクタ回路からの線をともに ANDゲートの入力にしてやれば,セレクタで指定したメモリだけから情報を読み出してくる仕組みを作ることも出来る.こうして,広大なメモリに自由にアクセスして読み書きができるわけだ.
しかし 1 回につき 1 ビットずつしか読み書きができないのではあまりに効率が悪いので,8 ビットほどをひとまとめに読み書きするようにした方がいいだろう.1 つのアドレスを指定するとそこには 8 ビットの情報が書かれている.それが現在のメモリ構造の原型になっている.「RAM」の誕生である.
メモリとは別に,メモリから読み出したデータを仮に保存しておくための場所もあったほうがいい.そういうものを一つではなく目的に応じて幾つか用意しておいてやると便利である.それは「レジスタ」と呼ばれる.例えば,A レジスタと B レジスタを加算器につないでおいて,結果が C レジスタに保存されるような仕組みにしておくこともできる.こうすれば,A レジスタと B レジスタに数字を入れることで足し算の結果が C レジスタに残るというわけだ.
メモリにアクセスするためのアドレスを専門に扱うレジスタもあったほうがいい.「インデックスレジスタ」である.このレジスタの数値はセレクタの入力に接続されていて,あらかじめここにアドレスの数値を入れてから読み込みや書き込みの指令を出せばその通りのことが実行されて,どこか別のレジスタにメモリから数値が読み込まれたり,どこか別のレジスタの内容がメモリに保存されたりするわけだ.
電気信号が作る一定周期のタイミングに合わせて 1 ずつ足し算をする回路を用意すればカウンターになる.このようなカウンターを実現するための専用のレジスタも用意してやろう.このレジスタの数値をセレクタを通してメモリに繋ぐと,0 番地から順にデータを読み出してゆく仕組みが作れる.このレジスタには特別な役割を与えたいので先ほどのインデックスレジスタを通さないで動くように独立させておこう.メモリにプログラムを入れておき,このレジスタが指し示すアドレスから順にプログラムを読み取るのである.このレジスタは「プログラムカウンタ」と呼ばれる.
プログラムカウンタが指し示すアドレスからデータを読み取る.それはただの数値に過ぎないのだが,その数値が 1 なら足し算を実行する,2 なら引き算を実行する,3 なら A レジスタの内容をそのまま D レジスタに移動する,4 なら A レジスタの内容をインデックスレジスタに書かれているアドレスに保存する,などのようにあれこれ決めておけば,その数値は命令としての意味を持つ.命令を読み取ったらそれをセレクタを通して,命令ごとにどれか 1 本の線だけに信号が入るようにしよう.その信号線をあちこちにつなげて,その信号が来たときにはその通りに実行されるように回路を組んでおけばいい.
プログラムの中には具体的な数値を入れておきたい場合もある.あとの計算命令に備えて,あるレジスタにその数値を入れたい場合などだ.そういう命令を受け取った場合には自動的に次のアドレスも読みに行くようにして,プログラムカウンタを 2 つ加算すればいい.次回は問題なくその次の命令を受け取れるようになる.
プログラムカウンタの数値を書き換える命令も用意しておけば,プログラムの実行順序をプログラム自身を使って変えられる.計算結果が 0 になっているときだけプログラムカウンタの数値が変わるような命令を用意しておけば,条件によってプログラムの進行手順が変えられるようにもなる.
このようにして,用意したプログラムを使って自動的に連続的に計算を実行することの出来る装置が出来上がった.基本的に出来ることといえば足し算や引き算,レジスタ間のデータの移動,メモリへのアクセスくらいだが,それをうまく組み合わせて手順よく実行してやれば,掛け算や割り算や,もっと複雑な計算も可能になる.
このような複雑な回路を全てひとまとめにしてくれてある IC というのも売っている.いや,これくらい大規模なものはもはや IC ではなく LSI と呼ばれるレベルなのだが,それが「CPU」だ.
多くの CPU はメモリは別になっており,メモリへアクセスするためのアドレスを指定する端子と読み書きするデータを伝えるための端子,読み書きの指令を伝える端子,CPU の外部とデータをやり取りさせるための端子(ポート)などが付いている.一定周期の電気信号「クロック信号」を作り出すための水晶発振子も外に繋ぐ.それでチップの周囲を囲むようにあんなに沢山の端子が出ているわけだ.(近頃の大型のCPUは端子が底面にびっしりという形になっている.)
そのうち,CPU も発達し,色んな命令が追加されてゆき,掛け算や割り算くらいならプログラムを使わなくても機械的に自動実行してくれるようなものが当たり前になっていった.
プログラムの発達
初期の古典的なコンピュータは,このように CPU の内部構造を把握した上で,職人的にプログラムが書かれていた.いわゆる「マシン語」「アセンブリ言語」などと呼ばれるものだ.装置の土台に近いレベルで動かすプログラムなので「低レベル言語」「低級言語」「低水準言語」などと呼ばれる.
しかしこれでは具体的にどんな計算をしているのかが分かりにくいし,CPU の構造が違えば全く流用が利かないものである.
そこで,もっと人間に分かりやすい形式で書いたものを,その CPU に合った形の手続きに自動変換してから実行するというプログラムが作られるようになっていった.それが「高レベル言語」「高級言語」「高水準言語」と呼ばれるものである.「FORTRAN」「COBOL」「LISP」「BASIC」「C言語」など色々と作られ,流行り廃りを経ながら,今でも新しい概念を取り入れたりしてどんどん種類が増えている.
量子コンピュータとの違い
さて,長い話になってしまったが,そろそろ量子コンピュータの話に戻ろう.古典的な論理ゲートと量子ゲートとの違いは入力や出力に量子ビットが使えることである.
古典的なコンピュータはプログラム的なことを自動で実行できるようになって使い途が拡がったのであるが,量子コンピュータはこのような方向への発展はしていない.古典的コンピュータに例えるならば「論理ゲートをこんなふうに組み合わせたら足し算ができるよね?」とか「引き算はこうすればいいよね?」みたいなことをあれこれ探している段階である.また,小型で安くて確実に動く量子ゲートを作るにはどうしたらいいかを試行錯誤している段階である.古典的コンピュータで起きたような次の段階への劇的な進化があるかどうかも予想が付かないし,発展のさせ方も分からないような状態である.
量子ゲートを使っても単純な足し算や引き算は実行可能だが,古典的な論理ゲートを使うよりも速いわけではないのであまり意味がない.せっかく量子ビットが使えるのだから,それを利用したもっとすごいことをやらせないともったいない.
古典的コンピュータでの様々な計算アルゴリズムというのは論理ゲートの組み合わせではなくプログラム言語の上で発達したものだった.一方,量子コンピュータの計算アルゴリズムというのは,量子ゲートをどのような組み合わせで接続したらすごいことを計算させられるかという意味である.少なくとも現在はそうだ.
もしこの先,量子コンピュータのためのプログラム言語が作られるにしても,目的に合わせて量子ゲートの組み合わせを自由につなぎ替えて,出てきた結果を拾うだけのようなものではないかと思う.もしそうなら,古典的コンピュータの下請けとしてたまに利用されるすごい関数といった位置づけだろう.今の自分の貧弱な想像力では,それくらいのことしか思い付かない.
次回は幾つかの量子ゲートとその機能を紹介していくことにしよう.











少しは知っておかないとね。