万能ゲートは本当に万能か？

制御ユニタリゲートを作る

1 量子ビットに対するユニタリゲートとCNOTゲートの組み合わせでどんな制御ユニタリゲートでも作れるという話をしたが,本当にそんなことが可能なのだろうか？今回はそれを調べる話に集中しよう.とりあえず次のようなゲート構成を考えてみよう.

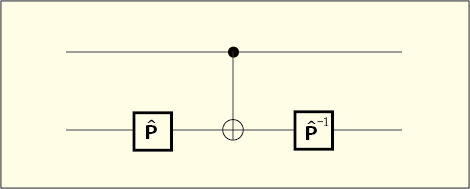
$\hat{P}$ というのは何らかのユニタリゲートである.ユニタリゲートの動作は 2 行 2 列のユニタリ行列で表せるから逆行列も存在していて,図中の $\hat{P}^{-1}$ というのはそれを実現するユニタリゲートである.

もし制御ビットが |0>} ならば標的ビットは何の変化も受けないので, $\hat{P}$ と $\hat{P}^{-1}$ を順に通って,結局何もなかったのと同じ結果になる.しかし,もし制御ビットが |1>} ならば標的ビットは途中でNOTゲート,すなわち $\hat{σ}_x$ による変化を受けて出てくるので, $\hat{P}$ , $\hat{σ}_x$ , $\hat{P}^{-1}$ の順で変化を受ける.行列の積で表せば,順に左へと掛けていくので, $\hat{P}^{-1}\hat{σ}_x \hat{P}$ である.もしあらかじめという条件を満たすように $\hat{P}$ が用意されていれば,これは $\hat{U}$ を使った制御ユニタリゲートと同等の結果になるわけだ！この方法でどんな $\hat{U}$ についても実現できるのではないだろうか？

いや,とても残念なことに (1) 式ではあらゆるユニタリ行列 $\hat{U}$ を実現できないのである.(1) 式の左辺の行列はどれもユニタリ行列であり,ユニタリ行列の積はユニタリ行列になるので,もちろん右辺もユニタリ行列である.そこまでは問題ない.しかしこの $\hat{U}$ には制限が掛かってしまう.どんな制限であるかを分かりやすく表すのはなかなか難しい.異なる $\hat{P}$ が同じ $\hat{U}$ を実現する形になっており,あらゆる形の $\hat{U}$ には結びつけられないのである.

P と U の対応関係を何とか分かりやすく表せないかと数日悩んでみたが,あまり見せたくもない結果に終わってしまった.U の行列成分の一つが必ず実数になってしまったりする.とにかく,1対1対応ではないのである.

この問題を解決するために回路を次のように組んでみよう.

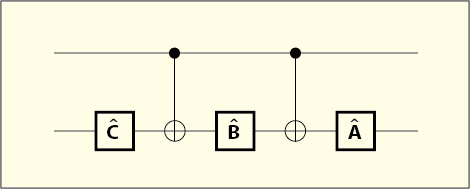
前回の話でCNOTゲートの働きを表す演算子として $\hat{C}$ を使ってしまったが,今回の話で使う $\hat{C}$ はそれとは無関係である.

そして,次の条件を満たすように $\hat{A}$ , $\hat{B}$ , $\hat{C}$ を定めるのである. $\hat{I}$ は単位行列である.理屈は先ほどとほとんど同じだから,何を意図しているかはもう分かるだろう. $\hat{A}$ と $\hat{B}$ を定めれば $\hat{C}$ は (2) 式によって勝手に決まる.実質,二つの行列を使って $\hat{U}$ を実現させようというわけだ.(1) 式よりも選択肢も増えたのでうまく行きそうな気はする.しかし本当に (3) 式を満たすような行列がいつでも見つかるという保証はあるのだろうか？

実はちょっとした問題がある.ユニタリ行列の行列式は絶対値が 1 になるという性質を持っている.それはつまり,1 あるいは -1 だけでなく,かも知れないし, $e^{iθ}$ で表されるなんらかの複素数である可能性もあるということだ.行列の積を計算した結果として得られる行列の行列式は,それぞれの行列の行列式の積に等しい.ここで (3) 式を見てみよう. $\hat{U}$ の行列式は左辺にあるそれぞれの行列の行列式の積で決まるということだ. $\hat{A}$ , $\hat{B}$ , $\hat{C}$ は 3 つの積が単位行列になるのだから,それぞれの行列式を掛け合わせた値は 1 でなければならないだろう.そして, $\hat{σ}_x$ の行列式はである.これが二つある.つまり $\hat{U}$ の行列式はこの方法ではにしかなりえないのである.そのような一部のユニタリ変換しか実現できないということである.

実は (1) 式でもこれと同じ問題があって,どう頑張っても行列式が -1 になるような行列しか作れないことが分かる.しかし (1) 式はそれ以前にどうしようもなく使い物にならなかった.つまり,行列式が -1 のユニタリ行列に限ってみても全てを表せない.それでわざわざ行列式の話はしなかったのである.

さて,この発想にこだわる限り,いくらCNOTゲートの数を増やしてみてもうまく行きそうにない. $\hat{U}$ の行列式の値はCNOTゲートの数によって決まってしまい,1 か -1 のどちらかにしかならないことになる.困ったものだ.

ユニタリ行列の復習

2 次のユニタリ行列の行列式が 1 になる場合とそれ以外になる場合とで一体何が違うのだっただろうか.

群論などで SU(2) という「行列式が 1 になるユニタリ行列」の話を考えたことは何度かあったが,それ以外の場合をあまり意識してこなかった.そういえば 3 つのパウリ行列でさえ行列式はどれも -1 なのだから SU(2) ではないのである.

行列式が $e^{iθ}$ になる行列の具体例を考えてみると,最も簡単なものとして次のような行列が思いつく. ありがたいことにこれはユニタリ行列でもある.これを行列式が 1 のユニタリ行列に掛ければ,行列式が $e^{iθ}$ のユニタリ行列が作れるわけだ.

しかしそれであらゆる種類のユニタリ行列が漏れなく作れるものだろうか？少し言い直そう.行列式が 1 であるような全てのユニタリ行列にこれを掛けるだけで,あらゆるユニタリ行列が作れるのだろうか？

群論的に言えばもっとすっきり表現できて,要するに SU(2) と U(2) の関係がどう結びついているかを考えているのである.

行列式が 1 であるようなユニタリ行列は次のような簡潔な表現でまとめられる. ただし |a|^2 +|b|^2 =1 という条件も要る.これを導くのは多少の手間が要るが,これで全ての状況を表し切れている.これに先ほどの行列を右から掛けると,次のようになる. この表現があらゆる 2 次のユニタリ行列を表し切れているかどうかだが,「ユニタリ行列は,互いに直交する単位複素ベクトルを表す縦ベクトルを並べたものである」という観点で眺めると確かにそうなっているし, $e^{iθ}$ が一方のベクトルに掛かっていることで二つのベクトルのあらゆる可能な位相差が表されていることも分かる.

群論的に言えば,SU(2) に exp(iθ) に相当する自由度が加われば U(2) になるという構造なわけで, exp(iθ) は U(1) と同じ構造の群だったから U(2) = U(1) × SU(2) と表せるのである.

ところで,先ほどから使っている行列は,どこかで見覚えがあると思ったら,少し前の記事に出てきた位相ゲートの働きを表す行列と同じものである. (3) 式では行列式が 1 になる行列しか作れないのだったが,これを組み合わせればどんな行列式を持つユニタリ行列でも作り出せる.すると,「制御位相ゲート」なるものを作ることができたら問題は解決に近付くのではないだろうか.次の図のように,前段にそれを設置するのである.

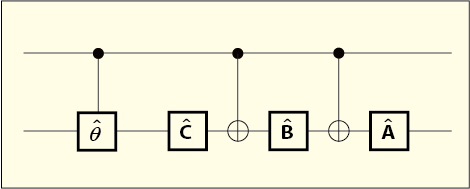
制御位相ゲートは制御ビットが |1>} の時に限って位相を変化させるので目的に適っている.

こうして問題は二つに分けられた.一つは,果たして (3) 式を使う方法で行列式が 1 の行列ならどんなものでも作り出せるという保証があるのかという問題.もう一つは制御位相ゲートを作る方法である.

制御位相ゲートの作り方

ここまでに考えた方法では,行列式が 1 や -1 になるユニタリ行列を使った制御ユニタリゲートしか実現の見込みはない.しかし先人が CNOT ゲートとユニタリゲートがあれば何でも作れると言っているのだから,何か方法があるはずだ.つまり,ここまでにやらなかった方法を試すしかない.制御ビットの方にもユニタリゲートを仕掛けてやるのである.

うまく説明できないので,試行錯誤した結果だけを見てもらうことにしよう.次のような構成にするとうまくいく.

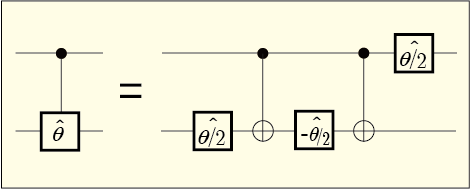
これでなぜうまく行くのかの説明は簡単である.まず,二つの量子ビットの状態が最初は次のような形で入力されたとしよう. 位相ゲートというのは |1>} の係数の位相だけを変化させるゲートだった.つまり最初に出会う θ/2 の位相ゲートは標的ビットが |1>} となっている項だけに働いて,状態は次のように変化する. 次に通るのはCNOTゲートだが,これは制御ビットが |1>} となっている項の係数を入れ替えるのだった.つまり,第 3 項と第 4 項の入れ替えである. さらにここで -θ/2 の位相ゲートに通す.先ほどと同じように第 2 項と第 4 項が影響を受ける. 再びCNOTゲートで第 3 項と第 4 項の係数の入れ替えをする. 最後に制御ビットの側に位相ゲートを通す.つまり,制御ビットが |1>} となっている項の係数だけが影響を受ける.それは第 3 項と第 4 項だ. こうして,第 4 項だけに $e^{iθ}$ の位相の影響を及ぼさせることに成功した.つまり,制御ビットが |1>} の時に限り,標的ビットの |1>} だけ位相をずらす機能を持ったゲートである.まさにこれが制御位相ゲートだ.

分かってしまうと意外と単純である.この考えで変形を繰り返せば何でもできそうな気がしてくる.

4次の行列を使う

制御位相ゲートの説明のために今行ったような係数の変化を 4 行 4 列の行列を使って表すことも出来る.制御位相ゲートは次のようになるだろう. これは (4) 式の状態 |Ψ>} が次のようなベクトルだと考えて,それに対して使うのである. ちなみに,CNOTゲートの機能を行列で表したければ,次のように書けばいい. これは (4) 式の第 3 項と第 4 項の係数を入れ替えるのと全く等価である.このようなものを作って次々と掛けていくことで,どんなゲートの機能も表せるだろう.

もう少し考えてみよう.1 量子ビットに働くゲートが次のように表されていたとしよう. これを標的ビットの方に入れたときの変化は次のように表せることになる. 制御ビットの状態に関係なく標的ビットが変化する様子が表されている.

制御ビットの方だけにゲートを入れたときの変化は次のように表せる. ちょっと分かりにくいかもしれないが,(4) 式で考えるなら,これは第 1 項と第 3 項の間だけで考えた係数の混じり合いと第 2 項と第 4 項の間だけで考えた係数の混じり合いを実現している.

ここまでの話にこのような行列を使うのは大袈裟だと考えて使わないでやってきたが,いちいち項の中身を見て,どの項とどの項が入れ替わるのかなどと考えて式変形を連ねるよりも,このような行列による機械的な作業に置き換えたほうが楽であることもあるだろう.

ここまでは量子ビットを 2 つまでしか考えなかったが,3 つになれば |0>}|0>}|0>}～|1>}|1>}|1>} という 8 つの状態の重ね合わせを考えることになる.そうなると 8 行 8 列の行列を使うことになるだろう.量子ビットが一つ増えるごとに状態の数は倍々に増えることになる.行列の次数も恐ろしく増えることになるわけだが,毎回手で計算するわけでもないので,行列の考え方を導入しておいた方が理論的にも扱いやすくなるはずだ.

任意の制御ユニタリゲートを作る処方箋

ではいよいよ最後に残った問題に決着を付けよう.行列式が 1 のあらゆるユニタリ行列が (3) 式の形で作れるかどうかというものだ.もうこれは量子コンピュータの話というよりも,面子を掛けて挑むような数学の話である.

しかし量子コンピュータに無関係だとも言えない.実際に量子コンピュータを作る場合には,欲しい機能を実現するためにどうやって $\hat{A}$ , $\hat{B}$ , $\hat{C}$ を用意したらいいかという具体例の一つでも知っておく必要はあるだろう.実用的であるかどうかはまた別である.

「行列式が1のユニタリ行列」という表現を何度も繰り返すのは面倒なので,ここからは群論で使われている SU(2) という表現をたびたび使わせてもらうことにする.この SU というのは Special Unitary の略である.行列式が 1 だという特別な条件を課した 2 次のユニタリ行列だという意味である.

多数の変数を使って確かめてみるという方法は,式が複雑になりすぎてうまくまとまらず玉砕した.

このノートでPQRと書いてあるのはABCのことである.この記事の仕上げ前の段階ではABCではなくPQRを使おうと思っていた.計算ミスの修正跡もそのまま残っている.

これは諦めて,オイラー角の考え方を使ってみることにしよう.球を回転させて別の姿勢にする回し方は色々とあるが,合計 3 回の回転角を適切に選ぶだけで,どんな姿勢にでも出来てしまうという定理がある.あらかじめ 2 つの回転軸を定めておいて,交互に回転させるのである.

ここで問題が生じる.ブロッホ球の任意の回転というのは行列式が 1 にならないようなユニタリ行列を含んでしまっている.今確かめたいのは行列式が 1 になる $\hat{U}$ を実現する方法が必ずあるかどうかということだけであって,そのためには話を簡単化して $\hat{A}$ も $\hat{B}$ も $\hat{C}$ も行列式が 1 になるようなものに限定して探してやれば十分なのである.

そこで,少しややこしい技巧を使う.現実の 3 次元空間での回転の座標変換をしたときに,電子のスピン状態がどのように変化して見えるかという状態変化は SU(2) の対象性があるのだった.つまり,行列式が 1 のユニタリ行列で表されるのである.このことを使って,3 次元の回転をユニタリ行列に対応させることにしよう.

分かりやすいように 2 つの回転軸として軸と軸を選ぶことにする.軸を避けたのは軸にはこのあとで特別な役目を負わせるためである.軸の周りでの角度の回転を R_y(α) と表し,軸の周りでの角度の回転を R_z(β) と表そう.そして次の式の右辺で表されるように交互に回転させれば,どんな姿勢にでも対応できるのだから,それを使って $\hat{U}$ を表してしまおう. この R_y(α) や R_z(β) というのは現実世界の 3 次元回転をイメージした記号だが,その実質はそれに対応する SU(2) の行列だと考えてもらいたい.

軸の特別な役割というのを説明しよう.軸周りでの 180°の回転をと表すことにすると, という関係が成り立っている.これは頭の中でイメージしてもらうとそうなっていることが分かるだろう.このも何らかの SU(2) 行列に対応しているのだが,具体的な話は後である.

ここで 3 つの行列を次のように選ぶ. すると, が成り立っているし, も成り立っている.これは (2) 式を満たしていることになるが,まだ (3) 式を満たしているとは言えない.が $\hat{σ}_x$ と同じかどうかが確認されていないからである.

それを確認してみよう.ここで空間の回転と SU(2) 行列との対応関係をはっきりさせる必要が出てくる.結論を言えば次のように表せる. これが導かれる過程については『スピノル（イメージ重視）』という記事で説明している.その記事では観測者が視点を回転させる立場で書いているのでこのような結果になるが,観測対象が回転する場合にはこの右辺の指数の肩についているマイナスは要らなくなる.どちらを使うかによってこのあとの計算が少し違ってくるが,ほとんど同じ議論になるから問題ないだろう.

R_x(θ) は次のように計算できる.途中で k=-(i/2)θ と置いて変形の手間を省いている. というのは R_x(π) のことだったから,この結果に θ=π を代入すれば求まる. 余分な係数が付いているだけでは $\hat{σ}_x$ とほとんど同じものである.これを (7) 式に代入すると,(3) 式と同じに……ならない？うまくいかないものだな.辻褄を合わせるために,(5) 式の右辺にマイナスを入れてやって $\hat{U}$ を作るようにしてやれば,(7) 式の右辺にもマイナスが必要になって,(3) 式と同じになるだろう.これで,どんな制御ユニタリゲートでも実現する方法があることが示せて,めでたしめでたし,だ.

目的は果たせたが,あまり実用的ではない気がする. $\hat{U}$ が (5) 式にマイナスを入れたものを使って必ず表せると書いているが,ここを具体的に考えるのは特に手間がかかるだろう.

もっと簡単にならないか？

これで今回の話を終えてもいいのかも知れないが少しだけ補足しておこう.最後の話でわざわざ 3 次元回転の座標変換を経由する必要性は説明したが,ブロッホ球の回転も同じイメージなのだから,直接オイラー角の考えを当てはめて同じことが出来るのではないだろうか.

そのようなことをすると行列式が 1 ではない場合も混じってきてしまうし,(3) 式を使う限りは行列式が 1 になるような $\hat{U}$ しか作れないのも既に分かってはいるのだが,なぜそのような直接的なイメージが利用できないのだろうか？

実はブロッホ球上では (6) 式のような分かりやすい関係が成り立たないのである.イメージだけで考えると普通の球と変わらないので成り立たない理由が分からないのだが,具体的なユニタリ行列を考えてやってみると余計な係数が付いてきてしまう.それで等式が作れないのである.

ブロッホ球というのは全体に複素数が掛かっていても同じ状態であると考えて,同一の点で表している表示法である.だから余計な係数が付いてきても気にしないというおおらかな態度を取れば何とかなるのかも知れない.しかしそういうゆるい議論をすると信用度が下がるし,どんな場合にどんな係数が付いてくるのかを調べるのも面倒になったのでやめておいた.そういう小手先の調整を入れる話をしていると議論のシンプルさが失われ,何をしているのか分からなくなってくるだろう.

今回の話では,行列式が 1 になるユニタリ行列ばかりを組み合わせた部分と制御位相ゲートとを別にするという構成で任意の制御ユニタリゲートが作れるという可能性を説明したが,少し冗長である可能性がある.うまくやればゲート数をもっと減らして構成できるだろう.

最小限のゲート数で望みの機能を実現するにはどうしたらいいだろうか.今回使った $\hat{A}$ , $\hat{B}$ , $\hat{C}$ などのゲートですら,位相ゲートやアダマールゲートを組み合わせて実現する必要がある.その辺りまで考えに入れるとかなり多くの調整が要りそうだし,あれこれ工夫する余地がある.どんな場合にどこまで減らせるかという条件を調べてみたり,素早く最適な構成を導くための実用的な手順を考えるのも面白いだろう.

私は今回の記事を書くためだけに数十ページの行列計算をしており,そのようなチャレンジをする前に少し長めに休みたい気分である.