量子力学：金属結合

金属とは何なのか

金属原子どうしはなぜ結合するのだろうか？貴ガスのように単独の原子として飛び回っているよりも,集まって存在していた方が安定する仕組みがあるはずである.

金属というのは「自由電子」の塊だと言える.一つの原子に束縛されない電子が金属結晶中を自由に行き来しているような状態になっている.原子の一番外側を回る幾つかの電子を引き止める力がかなりゆるいために,そういうことが起きるのである.

証拠は幾つか挙げられる.電気抵抗が小さいのは自由電子が大量に存在しているからである.少しの電圧を掛けただけでも電流が良く流れる.金属的光沢があるというのも金属の特徴だが,これも自由電子が原因である.ピカピカの金属表面を見るとき,それは電子の存在を見ているようなものだ.

光沢があるというのは光をよく反射するということに他ならない.電子気体というのは一種のプラズマであって電子密度が高いほどプラズマ振動数が高いから,ほとんどの振動数の光を表面でそっくり反射してしまう.一方,金属でない物質はそれほど電子密度が高くないので,電磁波が物質内部へ吸収されたり,透過したりする.
参考記事「プラズマは電磁波を反射する」

結合の腕の方向が強く定まっているわけではないから,変形させても簡単に折れたり砕けたりはせず,伸びたり曲がったりする.この性質は「展延性が高い」という表現がされる.熱伝導率の高さも電子によって説明される.

自由電子が飛び回る「電子の気体」の中に,正電荷を持った多数の金属イオンが沈められているというイメージで語られることもある.この金属イオンというのは,原子核とそれに束縛されて一体となっている多数の電子をまとめてそう呼んでいる.遊離した電子の分だけ少し負の電荷が足りていないから正電荷を持つ.このように,金属イオンと自由電子とに分けて考えると状況が把握しやすい.

このように寄り集まった状態は金属にとってなぜ居心地が良いのだろうか？なぜバラバラにならないで済んでいるのだろうか？残念ながらその仕組みを正しく解説できている記事はネット上ではほとんど見つけることができない.

よくある間違った説明

例えばこんな解説が良くある.金属イオンの間には正電荷どうしの反発力があるが,自由電子が間に入り込むので反発力が中和されて反発しないで済んでいるのだ,と.これは爆発的に分解しないでいることの説明にはなっているかも知れないが,残念ながら,互いに離れないで寄り集まっていることの説明にはなっていない.

今の話はさすがに説得力が弱いのだが,もう少し本当っぽく聞こえる次のような解説も良く見かける.自由電子はどれかの金属イオンに属するということなく,多数の金属イオンによってうすぼんやりと共有されている.すべての電子がすべての金属イオンを引っ張っているような状況になっているので一体になっていられるのだ,と.結果としてはそういう状況になっているのかも知れないが,なぜその状況になっている方が安定なのかが分からないままである.

自由電子だけのかたまりと金属イオンだけのかたまりがあれば,当然両者の間には引力が働くだろう.ところがそれぞれは単独ではかたまって存在していられないようなふわふわな存在だ.いや,それどころか,互いの反発力で飛び散るような存在だ.だからそれぞれのかたまりが引き合ってがっちり固定し合っているという考え方では無理がある.それぞれ単独では散らばろうとするような不安定なものが電気で引き寄せ合って集まっているだけであろう.結局,引き寄せ合っている力は正電荷と負電荷の間の力だけのようであり,電気的に中性になった金属原子がバラバラに存在している状況より有利な点があると言えるのだろうか？

ファンデルワールス力というものがある.電気的に中性な分子（または原子）の電荷分布が偏ることで,二つの分子が極めて接近したときにだけ,ごくわずかな電気的な引力が発生するというものである.ところが金属の場合には,自由電子が広域に分布しており,しかもばらばらであるので,多数の金属原子の集まりの中でそのような固定した電気的な偏りが維持できるとは考えられない.

共有結合はどうだろうか？あれは複数の電子を複数の原子核が共有して安定しているのだった.金属結合も似た状況だとは言えないだろうか？

残念ながら仕組みが大きく異なっている.共有結合は,量子力学的に説明が付いている.原子がバラバラに存在しているときよりもエネルギーが低くて安定した電子軌道が存在しているのでそのような結合状態に落ち込むのである.そこから再び互いに離れた状態になるにはエネルギーが必要なので,エネルギーを得るまでは結合したままの状態を保つのである.一方,金属結合の場合の電子はそのような安定した軌道を持っているわけではない.そういうわけで,金属結合を一種の共有結合であるかのように説明するのも正しくない.

今話したことは重要である.原子の結合というのは低いエネルギー状態に落ち込んだ状態だと言える.原子が互いに離れた状態へと変化するためにはエネルギーが必要で,それが足りていないから,エネルギーを得るまでは仕方なく結合を維持した状態にとどまっているのである.その点では金属結合も同じであるから,どうして集まっていた方がエネルギーが低くなるのかを説明しないといけない.

もう一つ,次のような説明も見かける.金属の塊というのは次のような箱形のポテンシャルを形成しており,近づいて来た別の金属原子はそこへ落ちるから引力が働いているのだという.

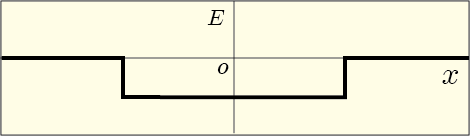
これは結果を説明したに過ぎない.このポテンシャルがなぜできるのかを説明しないといけない.金属イオンの集まりによる電気的引力だろうか？いや,全体としてはすでに電気的に中性になっているからそのような引力は働かないだろう.

簡単に言えばこれだけ

金属結合でエネルギーが低い状態が実現しているのは,実は電子の量子力学的な振る舞いが原因である.

電子には狭い領域に押し込められると運動量が増すという性質がある.位置が特定されると運動量の幅が広がるというイメージなので不確定性原理を思い出すかと思うが,不確定性原理そのものではないので,あまり不確定性原理という言葉を使うのも避けたいところではある.とにかく,金属原子どうしが繋がっていることによって自由電子が前より広い範囲に広がって存在できるようになると,運動量が小さくなる.つまり,運動エネルギーが小さくて済む.それで一個の原子内に電子が閉じ込められているときよりもエネルギーが小さくなるのだ.

そういう点では先ほど否定した共有結合でも似たことが起きていて,電子軌道がより大きな広がりを持っていた方がエネルギーが低くなっている.しかしあまり一緒にするのも誤解の元なので別物と考えておいた方がいいだろう.

理論的な説明

もう少し理論的な根拠をはっきりさせたいのなら井戸型ポテンシャルの問題を利用して考えるといいだろう.多数の金属イオンの正電荷が集まっている状況は大雑把に考えれば井戸型ポテンシャルのようなものである.電気的な引力があるので電子は金属のかたまりから容易には飛び出せなくて,井戸の中にとどまることになる.井戸の中にいる限りはそれほど力を受けないでいられる.

井戸型ポテンシャルの話はこのサイトでは書いていないが拙著『趣味で量子力学』が分かりやすくてお勧めである.大抵の入門書には出てくる話なので,ここであまり説明しなくても大丈夫だろう.

先ほど「箱型（井戸型）のポテンシャルがなぜできるかを説明しないといけない」と書いたのは金属原子にとってのポテンシャルの話であった.今話しているのは金属イオンの集団が作る「電子にとっての」ポテンシャルの話であるから,それとは別の話であることに気をつけよう.しかも,「もし金属イオンが集まって存在していたらどういうポテンシャルになって,そこでの電子はどういうエネルギーになるか」という仮定の話を考えようとしているのである.もしそういう状態が形成されて,その方が全体のエネルギーが低くなるのなら,その状態が安定状態として実現するであろう.

有限な深さの井戸型ポテンシャルで考えた方がより現実に近いが,あれは計算結果を簡単な式で表せないので説明に不向きだ.無限の深さの井戸型ポテンシャルの結果で代用しよう.その状況で電子に許されるエネルギーは次のように表される. この式は井戸の底で静止している電子のエネルギーを基準にしたものである.実際にはそのような電子は存在できないので n=0 という状態は存在しなくて, n=1,2,3,… である.この式は複雑に見えるかもしれないが, ΔxΔp≒h というのは今の状況では Lp ≒ h であり,これと E=p^2/(2m) を組み合わせればおおよそ似た形の式が出てくるわけで,大雑把に不確定性原理と電子の運動エネルギーという言葉で説明するのはそれほど的外れでもない.

この式を見ると幅が大きくなるほどエネルギーがどんどん下がっている.ということは,金属結晶が大きく成長するほど結合力が増すということだろうか？いや,それは大した問題ではない.エネルギーは下がって行ってもせいぜい限りなく 0 に近づくだけだから,単独でいる金属原子とのエネルギー差は一定の値で頭打ちになる.結合力はすぐにほとんど変化しなくなるだろう.

それより大きな問題は,結合する金属原子がどんどん増えるに従って電子がどんどん上の準位へと積みあがってゆくことだ.新たに参入する電子のエネルギーが高くなりすぎると結合するメリットがなくなってしまうではないか？！一方でが大きくなればエネルギーは全体的に下がるのだから,果たして,エネルギーが下がる勢いの方が勝つのか,上がる方が勝ってしまうのか？

実はこの問題は簡単に解決できる.今は 1 次元だけで考えているので,金属原子が一つ結合に参加するのは「が一つ増えて,が一定値増加すること」に相当する.とは比例という状況なのではいつでも一定値となる.エネルギー準位の上端は,結合する粒子数が増えようとも,ずっと変わらないままでいられるのである！

さらにもう少しこだわった説明

今のは 1 次元での簡略化した説明だったし,ちゃんと 3 次元で説明したらどうなるのだろうか？井戸型ポテンシャルを拡張して使うよりもフェルミ球という概念を使ったほうが話が簡単そうである.

金属中の電子はいわば気体のようなものである.自由に運動するのだが,フェルミオンであるので複数の電子が同じ状態を取ることができない.つまり,位置と運動量のどちらかは異なっていないといけない.そこで,3 次元の空間と,3 次元の運動量を一緒にした 6 次元の仮想的空間をイメージしよう.多数の電子はその 6 次元空間の一定範囲の中に詰め込まれており,同じ位置を占めることができない.

自由に動ける空間の体積は,金属結晶の体積で表すことが出来る.一方,運動量はというと,どの電子もエネルギーのなるべく低い状態を占めようとするだろう.その結果として次のような球状の分布になる.

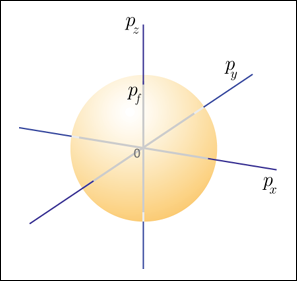
これを「フェルミ球」と呼ぶ.フェルミ球の半径をとすると,フェルミ球の体積は (4/3)πp^3 と表せる.このというのはこの電子の集団の中で最大の運動量の絶対値を意味する.新たな電子がこの集団に加わろうとする場合,すでに多数の先客が低いエネルギー準位を占めているので以下にはなれないのである.

結局電子は 6 次元的体積 V×(4/3)πp^3 の空間に詰め込まれていることになる.ここにどれだけの電子が同じ状態を取らずに収容可能だろうか？特に仕切りもなにもない連続的な空間の中で一体どの程度離れれば互いに異なる状態だとみなされるのだろうか？しかも位置と運動量は不確定性関係で結ばれており,値が確定せずにぼんやりと広がっている.

さて,これはとても不思議なことなのだが,量子統計力学の理論と実験との比較により,1 個の電子が主張する自らのテリトリーの体積は h^3 程度だということが分かっている.つまり 6 次元体積を h^3 で割ってやればいい.電子のスピンが異なれば別の状態だとみなされるので,さらに倍の電子が収容できる. ここから逆に電子数が個ある時のフェルミ運動量が求められる. さらにこれを電子の運動エネルギー E=p^2/(2m) の式に当てはめれば金属のフェルミエネルギーが求められる. が増えるというのは金属原子が結合に加わったことを意味しており,金属結晶の体積もに比例して増える.つまり,この式でも結合する粒子数に関係なくエネルギーは一定だということが言えるのである.

ところでこの式には 2/3 乗という面倒な形が出てくるが, V=L^3 だと考えれば先ほどの井戸型ポテンシャルで考えたのとほとんど変わらない状況であることが分かる.

念の為もう一つ補足しておくと,このフェルミ球の話ではまったく自由に振る舞う電子気体を仮定しており,それはエネルギー 0 から積み上がっていくイメージである.しかしこれら全ての電子は原子核の引力ポテンシャルに引かれているわけだから,そのエネルギーの底はマイナスになっていて,そこから積み上がっていっている.金属の塊は金属原子にとって引力となっているのだから,その底の部分から積み上がったエネルギーの上端でもまだマイナスだという状況なのだろう.

というわけで,「どうして金属原子どうしは結合するの？」と聞かれたら,「原子が単独でいる時よりも金属のフェルミエネルギーの方が低いからだよ」と返事しておけばすごく頭の良さそうなふりが手軽に出来るのである.

ところがそんなに単純でもない

と,まぁ,ここまで書いて意気揚々とこの記事を公開しようと思ったのだが,この話を裏付けるような実験データはあるのだろうかというのが気になってしまった.

ところがそれは簡単ではない.2 つの原子を引き離すときに必要なエネルギーのデータは見つかっても,金属の塊の表面から 1 個の原子だけを引き離すときに必要なエネルギーの一覧というのはなかなか見付けられない.1 個の電子を取り除くエネルギー（仕事関数）なら見つかるが,知りたいのはそれではない.

実際,どういう実験で測定したらいいものやら自分には思い付かないし,金属の塊の大きさによっても値は微妙に変わってくる可能性もあり,どういう条件に合わせたら良いのかも分からない.金属表面にある金属原子といっても,平らな面から 1 個だけを掘り出すように取り除くのと,平らな面に出っ張るように付いている原子を取り除くのとでは話が全く違ってくるだろう.

ごく僅かに探し当てたデータを見ても金属ごとにエネルギーが大きく違っており,ひょっとしてそれは実験方法の違いによるものかもしれないので単純に比較して良いものかどうかも分からない.例えば遊離した金属原子が金属イオンになっている場合もあり,その場合にはイオン化エネルギーの分だけ補正してやらなければならない.このように,分析に手間がかかる割には推測部分も多くなって,かなりの不確かさを含むデータになってしまうのである.

何か他のデータで代用できないだろうか？そういえば,金属結合の強さと言えば,金属の硬さなどに関係しているだろう.そこから考えてみたらどうだろうか？しかし金属にも極端に柔らかいものもあれば,相当に硬いものもある.先ほどの話だけでこの大きな違いを説明できるだろうか？そもそも金属の硬さとは何か？曲がりやすさとは何か？その違いは何によって説明できるのだろうかということも気になり始めてしまった.どうにも規則性が読み取れない.

これを調べるとなかなか面白いのである.金属の様々な性質は金属結合だけで説明できるものではないことが分かってくる.例えばタングステンの硬さの秘密は,自由電子だけではなく内側の電子も結合に関わっていたりするところにあるらしい.

先ほどフェルミ球のエネルギーの底はマイナスだという話をしたが,その深さは金属の種類ごとに違っているだろう.その底の部分のエネルギーの値を何とか簡単に導けないだろうか？ところがエネルギーの底と言っても平らなわけではない.金属イオンが並んでいて,そこから引力を受けているわけだから場所によってポテンシャルの高さがデコボコしているわけである.その辺りは専門の教科書ではどのように取り扱っているのだろうかということも調べようとして泥沼にはまってしまい,この記事の原稿はすっかり忘れ去られてしまっていた.

金属結合の話をするならいずれはイオン結合や共有結合についても書かなくちゃな,みたいなことを考えて,その仕組みを探っていくうちに今では分子軌道法にまで手を出して四苦八苦している.挑戦はまだ続いているのだ.

そう言えば,金属結合で原子間距離がどう決まるのかということも考えからすっかり抜けていた.なるべく原子間の距離が長くなって電子の移動範囲が広くなればなるほどエネルギーが下がるのだから得であろう.しかし離れすぎると今度は逆に,電子は原子から原子へと飛び越えるために余分なエネルギーが必要になるだろうから,両者のバランスの取れたところ辺りで安定しそうである.
実際には金属イオンが作る周期的ポテンシャル（デコボコの形をしたポテンシャル）の中での,金属結晶全体に広がる波としての電子のエネルギーを計算することになると思う.そうなるとクローニッヒ・ペニー・モデルやバンド理論の出番となるわけか.バンド理論のごくごく基本については拙著『趣味で量子力学２』がお勧めである.

こういうわけで,金属結合についてのいいかげんな解説は世に多いが,ちゃんとした説明がほとんどないのは,正確に説明しようとするとすぐに様々な問題にぶつかって挫折するからであろうということを思い知ったのである.