相対性理論：ブラックホールの見え方

この記事の動機

2019年4月10日の夜に行われた記者会見のネット中継で,人類が初めてブラックホールの撮影に成功したという知らせを聞いた.ピントがぼやけたドーナツのような画像であった.

それまで私はブラックホールを画像として捉えることができるなどとは想像していなかったから,ブラックホールが実際にどう見えるかという話題にはほとんど関心を持っていなかった.せいぜい SF のネタとして使える程度の知識だろうという感覚だ.人類が宇宙船で直接見に行くとしても私の生きている間には叶いそうにもない夢物語だろう.

ところが,世界中の電波望遠鏡をリンクさせることで,地球サイズの電波望遠鏡として使って,我々の銀河とは別の銀河の中心にある巨大ブラックホールを見たのである.見たと言っても,今回は可視光の領域ではなく,電波領域である.

想像画で見るのとはかなり違った.細かい星が見える宇宙を背景にして真っ黒い円があるような映像や,ブラックホールに吸い込まれる物質が眩しく光を放つ映像が印象に残っていたが,どちらでもなかった.赤くて濃いぼんやりしたドーナツである.もちろん,今回は電波領域だけを見ているので,映像の色も本物ではないし,見る振動数が変われば違った様相が見られるのかもしれない.

このドーナツの明るい部分がブラックホール周りのプラズマが放つ光であり,真ん中の暗い部分がブラックホールである.ただし,ブラックホールのシュバルツシルト半径は暗く写っている部分の 40 ％ほどであるらしい.

ブラックホールがどう見えるかについて現実味が感じられるようになったので,急に好奇心が湧いてきて自分も計算してみたくなったというわけである.

参考：「Event Horizon Telescopeによる超大質量ブラックホールの事象の地平面スケールの観測」

用語の説明

ブラックホールの周りを光が永久に回り続ける半径を「光子半径」と言ってシュバルツシルト半径の 3/2 倍であるらしい.この半径の球面を「光子球」(Photon Sphere) と呼ぶ.もしブラックホールが回転していればそれはもう少しだけ小さくなるようだ.

なぜわざわざここで光子という表現を使うのだろう？光子じゃなくて光でいいじゃないか？と思ったが,太陽などの恒星の表面を表す「光球」(photosphere) と区別するためなのだろう.

光のコースが光子半径を横切って内側に入ると,その光は必ずブラックホールのシュバルツシルト半径へと到達する.一度光子半径の内側に入ってから途中で抜けてくるということはない.光子半径の内側では光子半径の地点よりも時空が強く曲がっており,ブラックホールのある方向にしか曲がりようがないからである.光子半径の地点が,ぎりぎり,内側に入らずに周りを一周できる限界なのである.

無限遠からやってきた光がこの光子球に突入するような半径のことを「射影半径」と呼び,シュバルツシルト半径の (3√3 )/2 ≒ 2.6倍であるらしい.

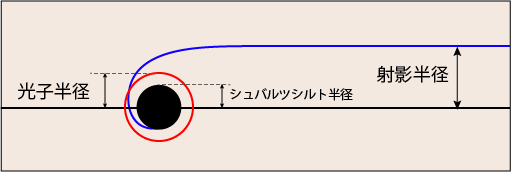
逆に光子半径近くから出てきた光は,無限遠まで進むとシュバルツシルト半径の 2.6 倍の円状に広がって分布するように見える.記者会見で,観測したブラックホール映像の黒い部分の40％くらいがシュバルツシルト半径だと思ってくださいと言っていたのは,1 / 2.6 ≒ 0.38 ≒ 40 ％だからだろう.記者会見では断定せずに少しばかり表現を濁しておられたように見えたが,ブラックホールの回転によっては比率が変わる可能性があるからかもしれない.あるいは今回得られた画像の解像度が十分ではないので,黒い部分の境界がどこにあるのかまだはっきりしないせいかもしれない.

今回撮像に成功したリングは,ブラックホールのごく周辺のガスから発せられたものだろうと分析されているが,もし光源がブラックホールから離れたずっと奥にあっても似たような黒い穴が映るだろう.例えば,ブラックホールの背景に一様な光源があったと想像してみよう.ブラックホールの向こう側から来た光は重力で曲げられて,光子半径以内に入ればブラックホールに吸収されてしまうし,光子半径のギリギリのところをかすめる形で吸収を免れた光は射影半径まで広がって観察されることになるからである.

射影半径の内側には決して光が見られないというわけでもないので注意が必要だ.ブラックホールのごく近くの物質から発せられた光は,光子半径の内側からであっても一部は脱出可能であり,射影半径より内側のコースを通ってこちらに向かってくることはあり得るからである.

ではそろそろ光子半径や射影半径をどう計算して求めたらいいのかを考えてみよう.

光子半径を求める

重力場中の光や物質の進路は測地線の方程式で表されているのだった.そこにシュバルツシルト解の計量を代入し,光の進路の場合にはさらに ds=0 だという条件を入れてやれば良い.

この作業は以前にもやったことがある.「光の湾曲」というタイトルの記事を読み返してみよう.

ずーーーっと読み進んで,(6) 式が出てくるところまで,まったく同じ議論が使えそうである.得られたのは次のような式であり,今回もそのまま使えそうだ. この式の中のはコースの軌跡を表すためのただのパラメータであり,物理的な意味は特にないのだった.

さて,光子半径というのはずっとブラックホールからの距離が変わらないままのコースなのだから dr/dσ =0 であり,これを代入すれば, というのがすぐに出てくる.こうして,光子半径はシュバルツシルト半径のぴったり 3/2 倍であることが導かれるのである.

射影半径を求める

射影半径を求めるためにはそのコースが光子半径以内に入るものを探せばいいということになる.いや,知りたいのは光の運命を決めるギリギリのラインがどこにあるかだから,光子半径にギリギリ接するという条件が必要になるわけか.しかしそれを式にどうやって当てはめて求めたらいいものだろうか.

ブラックホールから無限に離れた先ではコースは直線に近付いていくだろう.方程式を解けばそれは自然に出てくる話だろうからわざわざ仮定する必要はない.しかし,その直線をまっすぐブラックホールの方へと伸ばしたときにブラックホールの中心からどれだけずれているかという,いわゆる衝突径数との関係を取り込んでおきたい.

先ほど振り返って読んでみた記事の続きがそのヒントを与えてくれる.そこには次のような図が描かれていた.今回のために記号を変えて描き直しておこう.

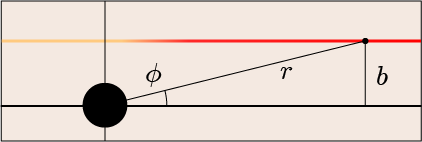
こうすれば,無限遠の極限では,ブラックホールからの距離と衝突径数の間に次の関係があることが言えるようになる. この角度は,無限遠では 0 である.この図の関係を取り入れるためには,をの関数 r(φ) として表すような微分方程式が欲しいところだが,先ほどの (1) 式をそのように書き換えると少し面倒な形の方程式が出来てきてしまう.やはり,以前の記事でやったのと同じように次のようなの逆数になっているような関数を新たに導入してやるのが良さそうだ. これを使うと,無限遠では次のような形の関係が成り立っていると言えるわけだ. u(φ) が満たす方程式を得るために,以前の記事の中の (7) 式が導かれるところまで同じやり方を真似しても大丈夫である.それは次のような式であった. この式にはなんら特別な物理的な仮定などは含まれておらず,安心して今回の問題にも使える.この式を解いてやるだけで光のコースは求められるはずなのだ.しかし,光子半径と接触するかどうかという条件をどう入れて解けばいいのかはまだよく分からない.

φ→0 で r→∞ ,つまり u→0 となっているのだから, u(φ) の初期条件として u(0)=0 を使って解くことになるだろう.もう一つ条件が欲しいところだが,無限遠では (2) 式を微分した u'=cosφ/b が成り立っているのだから, u'(0)=1/b という条件を当てはめてやればいい. (3) 式は非線形微分方程式なので初等的な関数で解を得ることはできそうにないだろうと早々に諦めて,コンピュータを使った数値計算を利用してグラフを描いてみた.すると,確かに初期条件のの値によって振る舞いが変わってくるのが分かる.の値が (3/2)√3 a を少しでも下回るとの値が発散するのである.はの逆数であるから,つまりやがてブラックホールに墜落することを意味する.

こうして,具体的なコースをコンピュータに描かせる手段は手に入った.しかし気になるのは,このスッキリした (3) 式のどこに, b=(3/2)√3 a という値が隠されているのかという点だ.

(3) 式を何とかもっと簡単に解く方法はないのかと思っていじってやる.よくある手として,(3) 式の両辺にを掛けて積分してやるというものを試してみる. ここで先ほどの初期条件 (4) と (5) を代入してやると C=1/b^2 でないといけないことが分かる.つまり,次のような新たな式が得られた. 非線形ではあるが一階の微分方程式になったし,もう簡単に解けてしまうのではないかと期待したがそう甘くはなかった.変数分離形の公式に当てはめて解こうとしたが,積分が複雑過ぎて諦めた.

ここで発想を変えてやる.ブラックホールに落ちるコースでははやがて 0 になる.落ち始めたら二度と半径が増えることはない.はその逆数なのだから単調に増加して無限大に発散するのである.念のために,その逆の場合も考えてみよう.ブラックホールに落ちないコースでは半径は一度は減っていくが,どこかで再び上昇に転じるはずである.

つまりこれらの違いは,が 0 になる瞬間がどこかにあるかないかという違いとして現れるだろう.(6) 式を移項すればであるから,この右辺が 0 になる瞬間が一度もないことがブラックホールへの墜落の条件となる.この (7) 式の右辺をで微分してやったものが 0 になるときに,この右辺が最小値になるのだから, であり,これを (7) 式の右辺に当てはめれば最小値が得られる. この最小値が 0 に触れるかどうかはの値によって決まり,ギリギリそうなる条件はというわけだ.こうして射影半径は光子半径のぴったり倍であることも導くことができた.