電磁気学：フレネルの式

異なる媒質間での境界条件

屈折率の異なる媒質の境界で,光線は反射や屈折を起こす.入射した光のエネルギーのうち,どれだけが反射して,どれだけが透過するのかは,電場成分や磁場成分の境界条件を考えるだけで計算できてしまうのである.

その境界条件というのはマクスウェル方程式から導かれるのだが,結論から言えばとても簡単である.

・境界面に平行な電場成分は連続でなくてはならない.
・境界面に平行な磁場成分は連続でなくてはならない.
・境界面に垂直な電束密度成分は連続でなくてはならない.
・境界面に垂直な磁束密度成分は連続でなくてはならない.

連続だというのはつまり,境界を挟んで向こうとこちらで値が同じでなくてはならないということだ.式で表した方が分かりやすいという人もいるかも知れない.境界面を z=0 の平面に設定しよう.第 1 の条件は次のとおりである. ここでというのは軸の正の方向から 0 に近付いた時の電場の値,というのは軸の負の方向から 0 に近付いた時の電場の値だというニュアンスだと思って欲しい.第 2 の条件も似たようなものである. 第 3 の条件は D_z(x,y,-0) = D_z(x,y,+0) であるが, D = εE であることを考えれば次のように書いてやってもいい. ここでというのは z<0 の側の媒質の誘電率で,というのは z>0 の側の媒質の誘電率である.同様にして第 4 の条件は次のように表せることになる. 電場やら電束密度やら 4 つの量が出て来てややこしいが,このようにして表せば電場と磁場を考えるだけで済む.

強磁性体以外のほとんどの物質はどれも透磁率が真空の透磁率にほぼ等しいので,最後の条件式から透磁率を外して考えても不都合が起こることは少ない.そうなると,磁場についてはどの成分についても連続であるという条件を考えればいいことになって簡単だ.そうなると磁場ではなく磁束密度で考えることにしても良くなる.

そのようなわけで多くの教科書では $μ=μ'=μ_{0}$ として計算しているのだが,この記事では敢えて透磁率の違いを考慮に入れて計算してみよう.どんな結果になるのか気になるからだ.もし手に負えそうになければ途中で逃げ出せばいい.出来るところまではやってみるつもりだ.

境界条件が成り立つ理由

これらの境界条件がどうやって導かれるかが気になる人もあるだろうし,全く気にならない人もあるだろう.気にならない人は読み飛ばしてもらっても全く問題ないが,飛ばし読みするほど難しくもない.

第 1 の条件である「境界面に平行な電場成分は連続」の説明からチャレンジしてみよう.まず,針金で作ったリングを想像し,半分だけ水に沈める.ここでは,異なる媒質の境界面を水面にたとえているのである.そこにマクスウェル方程式の一つであるファラデーの誘導法則 rot E+ ∂B/∂t =0 を使う.この式全体を,このリングが作る面の上で面積分してやる. この第 1 項はストークスの定理によって,リングに沿った線積分に直せたはずだ. このリングの形を小さな長方形にして,その面を軸の方向へ向けよう.リングを面内に置くのである.その縦の長さを,横の長さをとする.を小さくすればリングに囲まれた面積が小さくなり,第 2 項はどんどん 0 に近付くだろう.そして第 1 項の積分も,横の線の部分だけを計算すれば良くなり, となる.両辺をで割ってやれば E_x(x,y,a) = E_x(x,y,-a) となる.を限りなく小さくしてリングを平べったくしていっても成り立つべきなので,境界条件が導かれる.リングの方向を変えて考えれば成分についても同じことが言えるだろう.

「境界面に平行な磁場成分は連続」という第 2 の条件についてはアンペール・マクスウェルの法則 rot H- ∂D/∂t =i から導かれる.もちろん,境界面に電流は流れていないから右辺の電流密度を 0 だとするのである.そうすれば,上と全く同じイメージで磁場について同様のことが導かれる.

次は第 3 の条件「境界面に垂直な電束密度成分は連続」というものについて.これはマクスウェル方程式の一つであるガウスの法則 div D=ρ から導かれるのである.いや,ここではこれと等価な「積分形のガウスの法則」を考えてもらった方が楽だろう. 先ほどと同じように媒質の境界面を水面にたとえて,そこに静かに浮かぶ薄い板切れを思い浮かべてもらいたい.半ば水に沈んでいて,上半分は水の上に出ている.媒質の内部には多数の電荷が存在しているわけだが,全体としては正負の電荷が打ち消し合っており,境界面上にも単独の電荷はないものとしている.だからこの板状の領域の内側の全電荷は 0 であり,上の式の右辺は 0 である.

式の左辺の積分は,領域の表面から垂直に内部へと入るベクトル成分を足し合わせたものである.領域の厚みはどこまでも薄いものを考えれば側面についての積分値は無視できる.上面と下面の表面積をとして,板の上面と下面では積分の符号が逆になるから, となり,この両辺をで割ってやれば, D_z(x,y,-δ) = D_z(x,y,δ) となるわけだ.板の厚みを限りなく薄くしてやっても成り立つべきなので,境界条件が導かれる.

「境界面に垂直な磁束密度成分は連続」という 4 番めの条件も div B=0 から同様にして導かれる.

これで全てが導かれた.

光線の電場を式で表す

入射波,透過波,反射波の波数ベクトルをそれぞれ,, k'' で表すことにしよう.これらはそれぞれの波の進行方向を表してもいる.図にすると次のようなイメージだ.

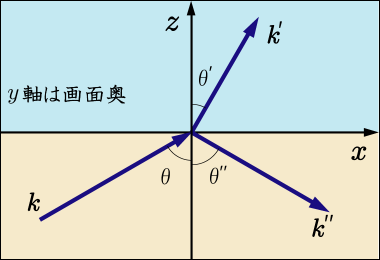
xz平面の左下から原点へ向けて入射した光線が右上への透過波と右下への反射波に分かれる様子を図示

}この図では入射角と反射角 θ'' が等しく描かれている.実際にそうであることは有名だが,この段階ではまだそのようなことは仮定するつもりはない.また,図を描くのを楽にするために,入射,透過,反射は同一の平面内で起こっているかのように表現しているが,この段階ではそのことも仮定していない.つまり,平面内を入射してきた光が反射したり,屈折して透過する際に,この面から逸れて左右どちらかに出て行く可能性もまだ残してある.しかしそのようなことは起きないことがこの後すぐに示されるだろう.

入射波,透過波,反射波のそれぞれの電場を次のように表すことにしよう. 波を指数表示で表しているのは,この方が計算が楽だからである.それぞれの波にタイミングのズレ,すなわち位相のズレがあった場合,振幅やが複素数になることでそのことを教えてくれるだろう.つまりやは複素数を成分に持つベクトルである.は透過波（Transmitted wave）の頭文字で,は反射波（Reflected wave）の頭文字である.

磁場を表すこともできるが,まだしばらくは必要ないので後にしよう.それより先に,条件をなるべく簡単にすることを考える.

「境界面に平行な電場成分は連続でなくてはならない」という条件があったのだった.それは E_x や E_y を使って確かめればいい.入射波と反射波は境界を挟んで同じ側にあるからその合計をして,それと透過波が z=0 において一致すればいいのである. E_x についての式を書けば次のようになる. 指数の肩が少しだけ軽くなっているのは (1) 式に z=0 を代入したものどうしで比較しているからである.この条件は境界面上のどこの点でも,いつでも成り立っていないといけない.つまりどんな,,に対しても成り立っていないといけない.その為には, であることが必要なのである.・・・などと言われても数学の苦手な私にはなかなかピンと来なくてしばらく悩むことになった.私と同じような人のために,このことについてもう少し詳しく説明しよう.

どんな値に対しても成り立つということは,例えば x=0 かつ y=0 であっても当然成り立っているべきであろう.そうするとずっと簡単になる. この式も全てのに対して成り立っていなければならないものだ.とはいうものの,ここまで簡単にしてもらってもまだよく分からない.全ての項を左辺に集めてしまおう. これなら何となく分かる.つまり,振動数の異なる 3 つの波形を重ね合わせることで波を完全に消せるか,という問題なわけだ.それはいかにも無理そうだ.どうしても波打ってしまう.しかしもしも ω=ω'=ω'' が成り立っていればという条件を満たすことで目的は達せられる.今はだけを残して考えたが,同様の思考方法で k_x や k_y についても全く同じ結論が得られるし,(3) 式が成り立っているべきことはいつも言えている.

ここでは E_x を例に取って (3) 式を得たが, E_y について考えても「全く」同じであって, という関係が得られるだろう.(3) 式も (4) 式も重要な手掛かりだ.しかしこれだけではまだまだ足りない.

ところで,少し妙な感じがしないだろうか.入射波が透過波と反射波に分かれるのだから, $E_{0}=T+R$ のような感じになっていてほしい気もする.しかし (3) 式や (4) 式はそういう形ではないし,境界条件から考えてもこれで間違ってはいなさそうだ.実際に二手に分かれるのは電場ではなくエネルギーなのだから,この段階でどうこう考えても仕方ないのか・・・.電場と磁場の両方が導けた暁には,ポインティングベクトルを計算することでそれぞれの波のエネルギー流量を計算して,ちゃんと辻褄が合っているか確かめてやることにしよう.

問題を簡単にする

今後の計算の負担を減らすため,あまり計算に関係のない要素は切り落として行くことにしたい.

先ほど (2) 式にあるように ω=ω'=ω'' であることを確認した.これは入射波も透過波も反射波も同じ周期で振動しているべきことを意味している.つまり (1) 式のそれぞれの波は共通して $e^{-iωt}$ を含んでいることになる.このことを忘れずにおいて,今後の計算に影響がない限りは時間変動についての表記を省略することにしよう.

さらに計算を楽にするために,入射波の進行方向を面に平行になるように選ぶことにする.それは k_y =0 になるように選んだということだ.ところが先ほど確認した (2) 式にあるように k_y =k'_y =k''_y でなくてはならないのだから,これらはすべて 0 だということになる.つまり,面内を通って入射した光は,右にも左にも曲がらず,面内で反射したり,透過したりするしかないことを意味している.最初に示した図の通りである.

単純な計算にもかかわらず,物理的な性質が制限を受けて色々なことが定まってきた.

さらに言えることがある.先ほどの図を見てもらうと分かりやすいが,幾何学的に k_x =|k|sinθ という関係になっている.これは他の場所にも言えて, k'_x =|k'|sinθ' や k''_x =|k''|sinθ'' である.ところがすでに (2) 式で k_x =k'_x =k''_x であることが言えているのだから,次のような等式が成り立つ. さて,この式の中で, |k| と |k''| は同じ媒質内の波の波数なので実は同じなのである.波の速度というのは v=ω/|k| と表せるのであり,もも等しければ,もちろん |k| も等しいと言えるわけだ.ということは θ=θ'' が言えて,「入射角と反射角は等しい」という有名な法則が導かれたことになる.

そしてさらに |k|sinθ = |k'|sinθ' からは, という関係が導かれる.屈折率というのは真空中での光速と物質中での光速の比として定義されていて n=c/v であるので,この関係は,それぞれの媒質の屈折率を使って次のように表すことも出来る. これが「スネルの法則」と呼ばれるものである.

ここまで,境界条件のほんの一部しか使っていないにもかかわらず,高校で学ぶ主要な話が導かれて来てしまった.では,残りの境界条件を考えると,他に何が導かれてくるというのだろうか？ここまでの話と辻褄の合わないことが起きたりはしないだろうか？とにかく計算を進めてみないと分からない.

さて,入射角と反射角は等しいということから図形的に k_z =-k''_z という関係になっていることも分かる.以上のことを考え合わせれば,(1) 式は次のように簡単に表しておけばいいということになる. ずいぶんとすっきりしてきたものだ.

偏光の問題

「境界面に平行な電場成分は連続でなくてはならない」という条件はすでに使い終えたので,今度は「境界面に垂直な電束密度成分は連続でなくてはならない」という条件を試してみたい.ここでやっとそれぞれの媒質の誘電率の違いを考慮することになるのだろうな・・・. ε E_z(x,y,-0) = ε' E_z(x,y,+0) という式を使って・・・.

待てよ？もし入射波の電場が方向には揺れてなかったらどうなるのだ？両辺は 0 だ.そういうことは起こり得る.

電磁波というのは横波であって,進行方向に対して垂直な面内で電場や磁場が振動している.今,入射波は図では右下に向かって進んでいるのでその面も斜めを向いていることになるのだが,軸方向にのみ電場を揺らしながら進んでくる場合というのも考えられるわけだ.これを「S偏光」と呼ぶ.この S はドイツ語で垂直を意味する「senkrecht」の頭文字だそうだ.入射面,つまり面に対して電場が垂直だという意味である.

一方,電場がそれに対して垂直方向に揺れながら進んで来ることも考えられる.その場合には電場は方向にも方向にも振動成分を持つことになって,考えるのが少しややこしそうだ.これを「P偏光」と呼ぶ.この P はドイツ語でも英語でも綴りは同じだが「parallel」の頭文字,すなわち平行である.電場が面内で振動しており,入射面に平行だという意味である.

さて,どんな光もこれら二つの偏光を組み合わせて表せる.二つの偏光の位相をずらして重ねてやることで,電場の向きがグルグル回るような円偏光も作り出せる.これは電磁場の振動の向きには本質的に二つの独立した自由度があるということなのだ.だからと言って,それらを場合分けして計算してやる必要があるだろうか？S偏光とP偏光に分けるのはいかにも人為的な分類にも思える.

あるいは一気にまとめて計算してやることは可能だろうか？その方が現実の電磁場を素直に表せている気もする.どう考えるのが効率が良いだろう？

この後の説明の方針を決めるのには相当迷った.最初は二つの偏光を場合分けして別々に計算するつもりでいた.S偏光の計算は軸成分の電場を考えるだけでいいので確かに楽である.しかしそこで一つの疑問が生じてしまった.まだ試していない軸成分についての境界条件はどう考えたらいいのだろう？入射波に軸成分が含まれていなかったとしても,透過波や反射波には電場の軸成分が生じて,それらが境界条件を満たすといったことが起きるかも知れない.何を言っているのかというと,つまり,入射波がS偏光だからと言って,透過波や反射波までS偏光になる保証はないのではないだろうか？ということだ.それを確認する計算はなかなか厄介だった.

P偏光になるとさらに面倒である.電場に成分と成分があり,まずはそれらと磁場との関係を考えてやらなくてはならない.いやいや,そういう考え方をしてもいいのだが,実はそんなことを考えなくても済む良い方法がある.P偏光の場合には,磁場成分が成分しか持たないことになるのである.電磁波では電場と磁場が互いに垂直の関係にあるのだから,S偏光とP偏光とで電場と磁場の立場が逆転するだけの話なわけだ.S偏光でやった話を電場と磁場を入れ替えて最初からやり直せばいいだけである.とは言うものの,ここまでやった話も含めて,もう一度式を立て直して同じ話を繰り返すのは面倒であろう.かと言って「同様に」などと書いて省略して済ますのも不安だ.透磁率は掛けるべきなのか割るべきなのか,電場から見て磁場は進行方向対して右回りの方向にあるが,磁場から見ると逆回りだから・・・,などのように微妙に異なる点もありそうだから全くの同じ話でもない.

この辺りのことを省いてシンプルにまとめている教科書は割りと多いようだが,「そんなことは自明ですよ,気になるのならご自分で試してご覧なさい」とばかりにその苦労の部分を隠しているのである.

そこで辿り着いた結論はこうだ.これら二通りの偏光を同時に入れて,一気に計算を進めよう.少々複雑にはなるが,苦労は 1 回で済む.

偏光を含めて電場の成分を書き表す

S偏光の振幅を E_s とし,P偏光の振幅を E_p としよう. E_s は軸に沿った成分なので特に問題はないが, E_p の方向についてはどう決めようか少し迷った.勝手に決めていい部分だ.結局は私の好みで次の図のようにした.

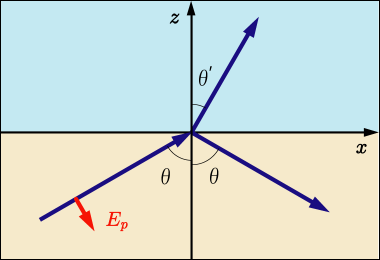
θ=0 の時に E_p の正の向きが軸の正の方向を向くようにという私の美意識に基いている.つまり, $E_{0}$ の各成分は次のように表せることになる. 透過波や反射波についても偏光があり,同様のことを考えねばならない.同様の基準に基いて,次の図のように方向を決めた.

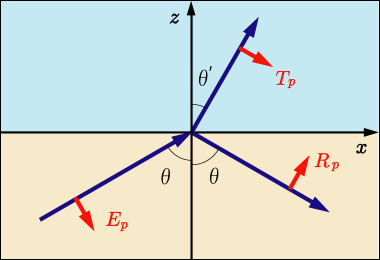
透過波のP偏光の向きの基準を右下に、反射波のP偏光の向きの基準を右上に選んだことを示す図

これにより,各成分は次のように表せることになる. (5) 式に当てはめてまとめれば,次のようである.

磁場の成分を計算する

電磁波の電場と磁束密度との間には |B| = |E|/c という関係があるのだった.また,電場の方向と磁場の方向と波の進行方向は互いに垂直である.例えば,もし電場が軸方向で磁場が方向だとすると,進行方向は軸の方向である.すると,外積を使って k×E で表される方向が磁場の方向だと言える.よって,磁場の大きさと方向を同時に正しく表そうとすれば次のようになるだろう. 今は入射波も透過波も反射波も面内にあるから k_y =0 であり, ということになる.これを使って入射波,透過波,反射波の磁場をそれぞれ計算してみよう.まずは入射波からだ. ここで, cosθ=k_z/|k | や sinθ=k_x/|k | という幾何学的に言える関係を使った.透過波については形式的に全く同じなので,結果だけ書いておこう. 反射波は一部だけ符号が違うので,丁寧にやり直そう. 結果だけまとめて並べれば次のようである.

境界条件を適用

こうしてまとめてみると,案ずるより産むが易し,意外すぎるほど簡単だった.あとは境界条件に当てはめるだけだ.まずは (6) 式を使って電場についての各成分の境界条件の式を並べてみよう. z=0 での値を使うので,実は後ろに付いている指数関数部分は全て共通であり,計算結果に寄与しないのである. そして (7) 式からは磁場についての各成分の境界条件が得られる.(7) 式は磁束密度で表しているので,磁場に変換するため,透磁率で割る必要がある.境界面に平行な成分であると成分についてはそのような操作が必要だ. 良く見ると,S偏光に関係する変数が出てくるのは (9) (11) (13) の 3 つの式であり,しかも (9) と (13) は全く同じ内容である.そしてP偏光に関係しているのは (8) (10) (12) の 3 つの式であるが,これらが独立であるかはすぐには判別し難い.よく調べてみると,実は (10) と (12) は等価なのである.先にそれを示してしまおう.(10) を変形しすると次のようになる. 単純な変形だが面倒くさい.一方,(12) を変形すると次のようになる. このように二つの式は同じ内容であることが分かる.

では先へ進もう.(9) 式と (11) 式を連立方程式と見て解いてやると,次のようになる. 結果を眺めてみてもそんなに楽しいものではない.そして,(8) 式と (12) 式を連立方程式と見て解いてやると次のようになる. なぜ (10) 式を使わないで (12) 式の方を使ったのかというと,なるべく式の中にとを残しておきたいからである.大抵の物質では $μ=μ'=μ_{0}$ という条件が成り立っているので簡略化して計算が進められるだろう.分子と分母で打ち消し合って,全て消滅するはずだ.(8) 式に入っていたはずの cosθ と cosθ' がどこへ行ってしまったかといえば,これはわざわざ k_z/|k | や k'_z/|k '| に置き換えて計算したのである.結果に統一感を持たせるためだ.

以上の結果から言えることがある.透過波も反射波も,入射波がS偏光ならS偏光だし,入射波がP偏光ならP偏光になるということだ.他にも言えるが,それは割りと当たり前のことである.入射波を強くしたら透過波も反射波も比例して強くなるだとか,入射波の強さによって透過と反射の比率が変わったりはしないだとかいったことだ.

色々なまとめ方

今導いた結果には k_z や k'_z が多量に含まれている.この形式にも利点はあるのだが,それは次回で分かるだろう.しかし普通に使う分には分かりにくい. cosθ=k_z/|k | や cosθ'=k'_z/|k '| という関係を使って徹底的に書き換えてやろう.そうすると今度は |k| や |k'| で一杯になってしまいそうだが,スネルの法則のところでやったように,これらの比は屈折率の比に置き換えられるのだった.それをうまく整理すると,いや,そんなにややこしいことはなく,ただ |k| をに, |k'| をに置き換えるだけでいいのである.結果は次のように書ける. おいおい,何だか,S偏光とP偏光とで対称性のある形にまとまったではないか.よく見ないと違いが分からないほどだ.

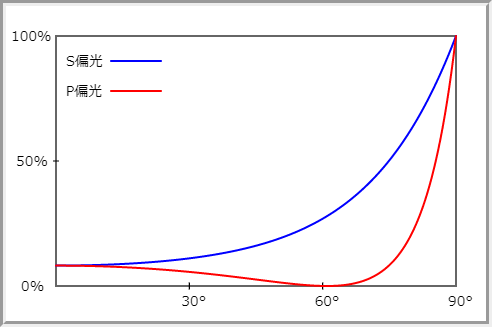
さらにスネルの法則を使えば,この式から屈折率を消してやることもできるが, sinθ や sinθ' だらけになってしまう.二つの透磁率に違いがないと仮定して消してしまえば三角関数の公式を駆使してまとめてやることもできる.なかなか大変なので,その結果だけ書いておこう. この式を見ると,どれも θ=0 のところで分子が 0 になってしまっているのだが,同時に分母も 0 になっているので 0 に近付く極限でどうなるかを見ないといけないのだろう.一つ面白いことが言えるのは,最後の R_p についての式だ.分母の tan(θ+θ') は θ+θ'=π/2 のところで無限大になる.これは透過波と反射波の向きの成す角が 90°だという状況を意味する.この時,反射波のP偏光は 0 になる.そう,P偏光だけ反射しない！この時の入射角のことを「ブリュースター角」と呼ぶ.物理的に何が起こっているのかと言われても,面白い説明が思い付かない.境界条件を満たしているに過ぎないわけだ.

ブリュースター角だけでなく,P偏光の反射はS偏光よりもいつも低い傾向がある.だから偏光グラスなどを使ってS偏光の成分を遮ってやると,水面からの反射の大部分をカットできる.反射の眩しさを軽減したり,反射光に紛れて見えにくくなっていた水の中がよく見えるようになるというので,釣り用のサングラスとして商品化されていたりする.興味のある人は「偏光サングラス」で検索してみるといいだろう.水だけでなく,車のガラスからの反射もかなり抑えられる.

エネルギー反射率

ここまでに見てきたのは,電場の振幅で比較した値である.エネルギーではない.入射波のエネルギーが透過波と反射波に分かれる割合を計算してやろう.

電磁波のエネルギーは電場の 2 乗に比例するのだった.正確には電場と磁場の積で表されるのであり,磁場の強さは電場に比例するので,結局は電場の 2 乗に比例すると言えるのである.ところが今回のように媒質が異なっていると,同じ電場であっても磁場の強さが違っていたりするので電場の 2 乗だけで比較するわけにはいかない.磁場と電場の大きさの関係は次のようになっている. だから入射波や反射波の電場の 2 乗には 1/(μv) を掛け,透過波の電場の 2 乗には 1/(μ'v') を掛けて比較すべきであろう.両者の比率だけを問題にしたいのならば,入射波や反射波の電場の 2 乗はそのままにしておいて,透過波の電場の 2 乗の方だけに μv/(μ'v') を掛けるようにしてもいい.

ところがこれだけでは正確ではないのだ.電場と磁場の積は,単位時間あたりに,単位面積を通過するエネルギー量を表しているのだった.そこで次の図を見てもらいたい.

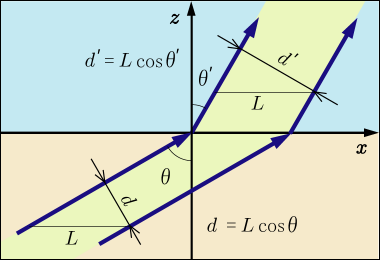
ある幅で入ってきた入射波は,屈折した結果,その幅がへと変化してしまうのである.例えば n'>n であるならば光線の幅は広くなり,それだけエネルギーは薄まってしまう.今のままでは単位面積を通過するエネルギーを計算しているので,薄まったエネルギーを計算していることになってしまっている.幅が広がった分だけ割増ししてやらないといけない.つまり,との比率である cosθ'/cosθ をさらに掛ける必要がある.

結局,透過波の電場の 2 乗に次のような因子を掛けて比較してやればいいということになる. この中のどれでも都合の良いものを使えばいいだろう.例えば (14) 式や (15) 式には一番右の形を使うと計算しやすいだろうし,(16) 式ならば左から 2 番目の形が良いだろう.これを使えば,S偏光については例えば, のような関係が成り立っているし,P偏光についてはのような関係が成り立っていることが確認できる.つまり,P偏光もS偏光もそれぞれにエネルギーの保存が成り立っていて,入射波のエネルギーは透過波と反射波に矛盾なく分配されていることが分かる.

エネルギーで考えた反射率を計算したければ E_s や E_p を 1 としてから計算すれば少し手間が省けるだろう.そうすれば R_s や R_p の式の 2 乗を計算してやるだけで良い.透過率の方は 1 から反射率を引いてやればいいだけだ.

次のグラフは屈折率が 1.8 の場合のエネルギーの反射率を表している.リンク先のウェブアプリでは屈折率の値をあれこれ変えてみることができるようになっているので,曲線が変化する様子を眺めてみて欲しい.

このようなグラフをいじっていてようやく気が付いたのだが,実はこの描画ソフトにこんなに多くのボタンを付ける必要は全くなかったのだ.例えば (16) 式の R_s でも R_p でもいいが,分子と分母をともに μ'n で割ってみよう.グラフの形は (μ/μ')(n'/n) という値だけに支配されていることが分かるではないか.大抵の場合は透磁率は無視して良いので「相対屈折率」 n'/n というものを導入してやれば良い.その値をコントロールするボタンだけあれば用は足りたのだった.

位相の変化

ところで R_s や R_p , T_s や T_p は全て複素数であると仮定していたのだった.もしこれらが虚数成分を持つならば,それは入射波 E_s や E_p に対して位相がずれていることを意味しているはずだ.ところが今回の結果を見ると,どれも実数のようである.これは位相のずれは一切起こらないと考えて良いということだろうか.

いや,そうではない.実は今回の話では幾つかの仮定が暗黙の内に使われており,それらの仮定は常に成り立つとは限らないのである.それらが成り立たない時,「全反射」と呼ばれる現象が起きる.そのような怪しい仮定が一体どこに紛れ込んでいるか分かるだろうか？その話は次回にしよう.

さて,今回のように暗黙の仮定がうまく成り立っている場合であっても,まだ位相がずれていないとまでは断言できない.今回の計算結果は複素数にはなっていないようだが,負になる場合がありそうだ.それは入射波に対して電場の向きが反転しているのであり,位相が 180°ずれていると言えるだろう.

透過波ではそのようなことは少しも起きていない.位相が反転する場合があるのは反射波だけである.

S偏光の場合には入射角より屈折角の方が小さい場合,すなわち,屈折率の低い方から高い方へと入射させた場合には常に位相が反転している.逆に,屈折率の高い方から低い方へと入射した場合には位相の反転は起こらない.

P偏光ではどうかというと,それよりも少しだけ面倒だ.基本的にはS偏光と同じなのだが,ブリュースター角で一旦反射は消え,それよりも入射角が大きくなると状況は逆転する.つまり,屈折率の低い方から高い方へと入射している場合には位相の反転は起こらず,屈折率の高い方から低い方へと入射している場合には位相の反転が起こるようになる.

なぜそのようなことになっているのかという具体的な理由を聞かれても,答えるのは難しい.境界条件を満たすにはそうでなければならない,としか言えそうにない.

空気中から水やガラスのようなずっしりとした媒質に入るときには固定端反射のようなイメージで位相が反転し,逆の場合には軽い媒質に入るので自由端反射のようなイメージで位相はそのままだという連想はできる.しかしP偏光のブリュースター角以上での反射はそのイメージを裏切ってしまっている.

本当はこの辺りの位相が反転する現象が起こる理由をはっきりさせたくてじっくり考えてきたのだが,うまく説明ができず情けない限りだ.そう言えば,固定端反射では位相が反転し,自由端反射では位相がそのままだという理由も,自分は未だによく分かってないような気がしてきた.