物理数学：線積分

線積分のイメージ

高校の積分では積分範囲が数直線の上に乗っていた.何を言っているか分からないかも知れない.当たり前過ぎることというのは,言われてもピンと来ないものだ.つまり,1 変数の関数 f(x) があって,その f(x) のグラフの曲線と軸とに挟まれた領域の面積を求めるというのが積分のイメージであった.定積分の積分範囲というのは,軸という直線の上のどこからどこまで,という形で指定されていたのだった.今からその常識を飛び出すことにしよう.

2 変数の関数 h(x,y) というものを考える.この関数は土地の起伏を表しているようなイメージである.地図上の位置を (x,y) で指定してやると, h(x,y) がその地点の標高を返してくれるのだと考えれば分かりやすい.関数名としてを使ったのは高さ(height)の頭文字だからである.

これからこの関数 h(x,y) を積分しよう.積分範囲は・・・,そうだな,「この平面の上を走る自由な曲線コース」！

自由な曲線コースの上を進みながら積分する・・・.これが「線積分」である.もちろんそれを計算するためには,その曲線を具体的に指定してやらないといけない.しかし一体,どう考えて,何を計算したらいいのだろうか？これまで軸というカチカチのレールの上で積分を計算することしか知らなかった人にとって,この自由さにはかなり面食らうと思うのだ.

まずはイメージを説明しておこう.積分コースに沿ってうねるように立てられた衝立（ついたて）のようなものを考える.

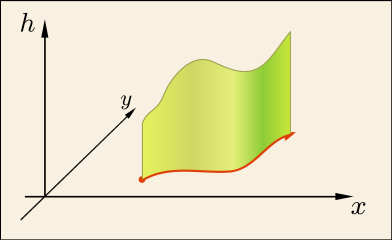
この衝立の高さはその地点での h(x,y) を意味している.線積分で計算したいのはこの衝立の面積である.直線上での積分の素直な拡張だと言えるだろう.

具体的な計算の方法

このようなものを計算するにはどう考えたらいいだろうか？ (x,y) 平面上を走る曲線レールを細かく分割してやると,その一つ一つはほぼ直線だとみなせるようになる.「その微小な長さと,その近くでの h(x,y) の値とを掛け合わせたもの」を考えれば,それは衝立を微小な短冊状に切ったものの面積を表すことになる.それらを全て合計すれば,望むものが得られるはずである.

この計算をするには,コースの形がの関数になった x(t) と y(t) とで表されていると都合が良い.コースのスタート地点が $\big(x(a),y(a)\big)$ であり,ゴール地点が $\big(x(b),y(b)\big)$ であり,その途中での位置が a≦t≦b であるようなによって $\big(x(t),y(t)\big)$ で示されるようにする.これはコースが最初からそのような形式で指定されることもあるし,そうでなければ計算者が与えられたコースを何とかこの形式で表せるように工夫することになる.

変数は時刻であるかのようなイメージである. t=a でコースを出発した点が,紆余曲折を経て, t=b でゴールに辿り着くのである.この点はコース上を一定速度で進む必要はない.ゆっくり進む部分もあれば素早く駆け抜ける部分もあるだろう.コースの形が表されていればそれでいいのである.もちろん,なるべくシンプルな形に表した方が計算が楽になるだろう.

時刻から t+Δt までの微小な時間内にコース上の点が動く距離を考えよう.最初 $\big(x(t),y(t)\big)$ にあった点が $\big(x(t+Δt),y(t+Δt)\big)$ にまで移動することになる.微小な時間だから,ほぼ直線的に移動したものと考えても良い.すると移動距離はピタゴラスの定理によって, と表せるだろう.いやしかし,これではあまりに複雑そうだ.もう少し簡単に直せないだろうか.ほぼ直線的に変化しているのだから x(t+Δt)-x(t) の部分は dx/dt Δt と近似できそうだ.成分の変化についても同様であり, のように書ける.が無限に小さいと考えれば,近似ではなく次のように表してもいいだろう. このが微小時間に点がコース上を進む微小距離である. x(t) と y(t) が具体的に分かっていればこれは楽に計算できて,のみの関数として表されるだろう.高校までの 1 変数の関数 f(x) を積分するときのに相当する部分である.

あとはこの地点での h(x,y) の値がどうなるかを考えるわけだが,それはの時と t+ dt の時とでほとんど同じ値だろうから h(x(t),y(t)) を使えば良い. x(t) と y(t) が具体的に分かっていればこれものみの関数として具体的なものが得られるだろう.

結局は次のような計算をすれば望むものが得られることになる. 見た目はややこしいが,具体的な h(x,y) の形と具体的なコースの形とを代入すれば,変数による普通の積分をすれば良いだけになる.

ここではコースのスタートとゴールを t=a と t=b で表したが,積分範囲が 0≦t≦1 となるようにコースを表すことが出来たならなお計算しやすくなるだろう.

コースの制約

今導いた線積分の公式の中には x(t) と y(t) を微分したものが出てくる.ということは, x(t) と y(t) とはどちらも滑らかでないと微分が計算出来なくて都合が悪いだろう.滑らかなコースを選ばないとこの計算が出来ないことになりそうだ.

しかしコース上の幾つかの地点に角張ったところがあっても大丈夫だ.微分は出来ないのだが,そこでコースを分割してやって,別々に計算して,後で足し合わせればいいのである.

3 次元での線積分

以上の話は 2 次元コースでの線積分だった.これを 3 次元に拡張することは簡単である.3 変数の U(x,y,z) という関数を考え,これを,3 次元空間を自由に飛び回るコースで積分するのである.

この計算が意味するイメージを図に描くことは私には無理である.下手に図にすればかえって難しくなる気がする.類推してもらうしかない.

要するに,「3 次元コースを走るレールの微小な長さと,その近くでの U(x,y,z) の値とを掛け合わせたもの」をコースの端から端まで和をとって進んで行くのである.考え方は同じで,次のような計算をすることになる.

ベクトル量の線積分

線積分というのは基本的にはたったこれだけの話だから,以上をワンセットの知識として頭の中へ収めておいてもらえばきれいに片付くだろう.しかし物理ではベクトルの概念と組み合わさった形のもう少し変わった線積分が出てくるので,これだけで線積分が完全に理解できたと喜ぶのは早い.

その辺りは後で「ベクトル解析」の一部として説明することにしよう.分けて考えればそれほど難しくもないと思うのだ.