極座標(円座標)
前回の記事では微小面積や微小体積
を分割するときに,徹底してデカルト座標を使ってきた.「デカルト座標」というのは座標軸が直線で互いに直交しているという,中学や高校の数学でも使っているごく普通の座標のことである.
デカルト座標のことを,直交座標とか,より正確に「直交直線座標」だとか呼ぶこともある.(軸が曲線だけど互いに直交するような「直交曲線座標」というものもあるからである.)英語での表現をそのまま使って「カーテシアン座標」と呼ぶこともある.英語では「デカルトの」という形容詞は Cartesian (カルテジアン/カーテシャン)と綴るからである.人名のデカルトの綴りは Descartes だが,Des の部分はフランス語の冠詞にあたるので省かれているわけだ.
要するに,前回はや
を次のように表現し直して計算したのであった.
さて,デカルト座標の他にも座標軸の引き方は色々あって,有名なのが,原点からの距離
と方位
で表す「極座標」というものである.

極座標で表した点とデカルト座標で表した同一の点
との間には次のような関係が成り立っている.
このような極座標で,座標値である二つの値
をともに少しだけ動かすことを考えよう.その幅をそれぞれ
と
で表すことにする.その様子は次の図のようになるだろう.
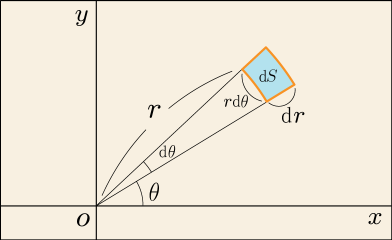
この図の水色の部分の面積は正確に計算すると
となるわけだが,第 1 項は微小量が 2 つ掛け合わされて出来ているのに対し,第 2 項は 3 つの微小量が掛け合わされており,一つ多い.つまり微小量が無限に小さい極限を考えると,第 2 項は第 1 項よりもずっとずっと小さくて無視できるほどになる.
図を見てもの部分は縦と横の長さがそれぞれ
と
であるような長方形に似ていることが分かるだろう.長方形には見えないかもしれないが,微小幅を無限に小さくするとほぼ長方形だとみなせるようになり,長方形とのズレはどんどん無視できるようになる.このような無数の微小面積の集まりとして平面を埋め尽くす様子をイメージすれば,面積分が出来そうだ.
のように表して計算すれば良いのである.
例えば半径の円形領域で関数
を面積分したければ,
のような計算をすることになる.積分範囲が円形をしている場合には,このように極座標を使った方が範囲の指定がとても楽に出来る.
さらに関数が原点を中心として回転対称な関数である場合には,関数は
には関係のない形になっている.つまり実質
ということなので,計算はずっと楽になるだろう.被積分関数の中に
が含まれていないのだから,次のように
の積分だけ先にやってしまえる.
このように,積分範囲の形や関数の形に応じて計算に最も都合の良い座標を選ぶことが重要になってくるわけだ.
3 次元極座標(球座標)
3 次元にも極座標がある.やはり原点からの距離と角度で位置を指定するのだが,次の図のように考えるのが一般的である.
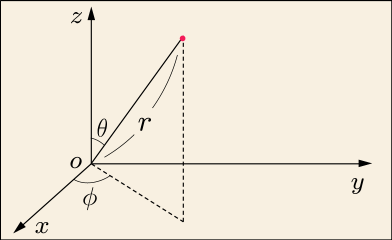
これは地球上の位置を表すときの緯度と経度に似ている.は緯度に似ているが,赤道を基準に北と南にプラスマイナスで表すのではなく,北極を 0 として 180°の範囲で動くところが違う.つまり
の変域は
である.
は経度に似ているが,東経や西経があるわけではなく,
の範囲で一周することになる.
同一点を表すと
の関係は次のようになっている.
慣れるために,本当にそうなっていることをちゃんと確認しておいてほしい.図で
平面上に描いてある点線の長さが
であることに気付けばあとは簡単だろう.
さて,先ほどと同じように微小範囲のことを考えてみよう.少しややこしくなるが根気よく考えて付いて来てほしい.の点から
の幅だけ増加させた時に新たに出来る微小範囲は次の図のようになる.
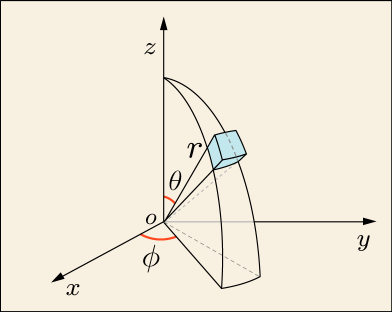
これは幅を無限に小さくする時には縦,横,高さがそれぞれ,
,
の直方体だと考えることができる.図がややこしくなることを恐れて情報をあまり書き込んでいないが,どこの長さが幾つになるか分かるだろうか?初めて見た人にとっては簡単だとは思えないから,パズルのようなものだと思ってじっくり考えてほしい.
順番に考えれば簡単だ.が微小量
だけ伸びる方向というのはすぐに分かるだろう.次に
がどこの角度のことかを確認したら,それがわずかに
だけ増加するというのがどこを指しているかも分かる.その角が張る円弧の部分が
だ.もう一つの辺の長さがなぜ
なのかは,少しややこしい.どこが
でどこが
であるのかが分かれば理解できるだろう.
これにより,微小体積を次のように解釈することができるようになる.
これを使って積分範囲の空間を埋めることを考えれば,前回複雑に範囲指定した半径 1 の球状の体積分は次のように表せる.
というのは
の各変数を極座標の変数に書き換えて出来る関数のことだが,(1) 式を使えばいい.面倒なのでこのように表すことにした.もとから
の関数として表されたものが与えられていればそのまま使えばいい.関数の形によっては前回デカルト座標でやったよりもずっと簡単に計算できそうだ.
を使って半径
までの範囲で計算すれば,これまで公式として暗記していた球の体積が簡単に導き出せる.また天体の密度が半径だけで決まると考えてそれを
で表せば,天体の全質量が計算できたりもする.
円筒座標(円柱座標)
3 次元空間の座標としてよく使うのが他にあるので紹介しておくとしよう.
面内での位置を 2 次元極座標のように
と
で表し,
方向の位置をデカルト座標の値をそのまま使って
で表すやり方である.これを「円筒座標」あるいは「円柱座標」と呼ぶ.
これで話が通じているか少し不安なので念のため言っておくと,は原点からの距離ではなく,
軸からの距離を表していることになる.デカルト座標との関係は次のようになっている.今回は図はないので,自分の理解が正しいかどうか確認してもらいたい.
さて,この座標を使って微小領域を考えると次のようになる.
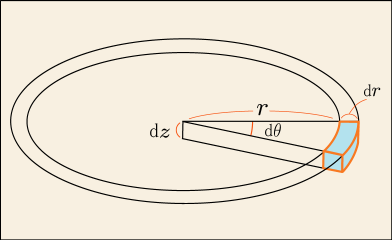
つまり微小体積は次のように表せるということになる.
あとは同じ事だから積分の仕方などはもう言わなくてもいいだろう.
2 次元座標の紹介
他にも座標の種類は色々とあるのでざっと紹介しておこう.ただし簡単に済ませたいので 2 次元に限定することにする.
座標軸が直交していないような座標の取り方もあることを話しておきたい.次の図のように軸だけが傾いているようなものを考えよう.
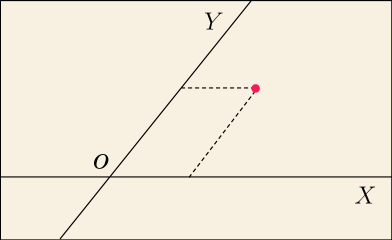
これは最も単純な「斜交座標」の例である.この座標では軸に平行な多数の線と,
軸に平行な多数の線によって座標を読むことになる.つまり,ある地点の座標を読みたければ,図にある点線のように線を引いて,それぞれの座標軸に書かれた数値を読むのである.
この座標で表現された位置とデカルト座標で表された位置
との関係はややこしいので書く気が失せた.今回の話とは関係ないし,わざわざ書くほどのものでもない.知りたい人は自力でやってみると頭の体操になるだろう.
この他に楕円座標や双極座標なども紹介しようと思っていたが,もともと詳しく説明する気はなかったし図を描くのが大変だったのでWikipediaへのリンクでごまかすことにした.そんなものもあるのだな,というくらいに眺めてもらったら良いと思う.
ヤコビアン
このように色々な座標の取り方があることが分かったと思うが,そのたびに図を描いて微小面積や微小体積がどう表せるかを考えるのは面倒である.もちろんそういうイメージをしっかり思い描くのは大切なことなのだが,時には具体的なイメージがそれほど重要でないこともある.単にその場限りの計算の都合で,ある座標を導入した方が楽に計算できるとかいう場合だ.
そういう場合に便利な,微小面積や微小体積の表し方を機械的に導く方法がある.3 次元極座標を例にして考えてみよう.次のような行列を考える.
このような行列を「ヤコビ行列(ヤコビアン)」と呼ぶ.ここに (1) 式を具体的に代入し,その行列式を計算してみよう.
先ほど 3 次元極座標を紹介した時に見た微小体積の因子が計算だけで導かれてきた.なぜこんなことが出来るのだろうか?
行列式の意味というのは,各列,または各行の成分をベクトルだと見た時に,それらのベクトルが作る平行六面体(2 次元の場合には平行四辺形)の体積(面積)を表しているのだった.ここでは縦一列を一つのベクトルと見て考えてみよう.
というベクトルは,変数
が増加した時に,その様子がデカルト座標ではどの方向に増加するように見えるのかを表すベクトルである.
だけ増加した場合には,そのベクトルに
を掛けたものがデカルト座標での変化量になるが,ここではまだ掛けられてはいない.このヤコビ行列の中には,同様に,
が増加した場合のデカルト座標での方向,
が増加した場合のデカルト座標での方向を表すベクトルがあり,
というのはそれらに挟まれて出来る平行六面体の体積を表していることになる.
や
や
がわずかに変化するときに,その体積は
や
や
に比例するのだから,
と表されることになる.これはデカルト座標における長さの指標で測った微小体積
を意味するので,デカルト座標で表現された積分を次のように書き換えることができるだろう.
これを見ると,あたかも次のような関係が成り立っているかのように思えるが,そういうわけではない.
この (3) 式の左辺はデカルト座標での微小な直方体領域の体積であり,一方,右辺は極座標の変数を動かした時に出来る形の微小体積であり,それぞれの微小体積の大きさは互いにまるで関係がない.関係ないのだから,等号でつなぐようなものではない.ここまでの説明はあくまでも (2) 式のような積分の変数の変換の形にして成り立つ話である.
・・・とは言ったものの,今回のような直接的イメージに頼るのではなく,もう少し抽象的な解釈を取る場合には (3) 式のような表現をするのも許容範囲だという意見もある.ただし特殊な考え方で扱わねばならず,その意味の分からぬままにこの表現を一人歩きさせることは混乱の元だと私は思う.
多様体論などを学び微分形式というものを理解したり,ルベーグ積分などを学び測度というものを理解すると,この辺りの雰囲気が良く分かるようになるのだそうだ.
(2) 式のような変換が可能だとは言っても,積分範囲が複雑な形をしている時には,ちゃんと対応する範囲を考えて積分範囲を考え直さないといけないので大変ではある.しかし積分範囲が空間の全体だったりすることもよくあり,その場合には何も考えなくていいからとても楽である.
ヤコビ行列の行列式
のことを「ヤコビ行列式」と呼ぶ.先ほど,ヤコビ行列が出てきたところに括弧書きでヤコビアンと書いてあったが,ヤコビアンと言えばヤコビ行列式のことを指すこともある.ヤコビアンというのは「ヤコビの」という意味だからどちらにも使うわけだ.
ヤコビアンをと書く代わりに次のように表記することもある.
これはヤコビアンが偏微分の拡張だというイメージを強調するような記法である.そのイメージを持っていれば,もしヤコビアンの定義を忘れてしまってもすぐ思い出せるだろう.(3) 式の形を思い出せば間違えない.また,行と列のどちらがどうだったかという部分が思い出せなくて悩むことは良くあるが,それで計算を中断する必要はない.行列式の計算は行列が転置していても同じ結果にたどり着くからだ.
積分の変数変換
ここではヤコビアンの例としてデカルト座標と 3 次元極座標との間のことを考えたわけだが,いつもデカルト座標を介する必要もない.同様の理屈は他の座標系どうしでも成り立つことになる.
というわけで,このヤコビアンの目的は単に微小体積の表現の仕方を導くだけにはとどまらない.重積分するときの変数の組を別の変数の組に置き換えるという目的にも広く使えるのである.変数の変換規則さえ分かっていればそれを使ってヤコビアンが計算できるだろう.(2) 式は変数が変わってもそのまま使える式である.
高校でやった置換積分
今,ヤコビアンが重積分の変数変換に使えるという話をしたが,1 変数の積分の場合にも当てはまる.高校の数学で置換積分と呼ばれていたものがまさにそれだ.
置換積分は高校で習った時にはとても分かりにくかった気がするが,ヤコビアンの最も単純な場合だと考えれば実に簡単な話だ.その場合のヤコビアンは 1 行 1 列になり,変数が一つだから偏微分で表す必要もなくなり,ただの微分になる.
例えば,元々変数がだったものを,別の変数
を使ったものに書き換えたければ,
と
の関係が
のように書けるものだったとして・・・.そうか・・・なるほど.具体的に説明しようとすると高校の教科書と変わらない説明になってしまうのだな.面白くないからやめておこう.言いたいことは伝わっただろう.










