留数だけを簡単に求める方法
留数さえ求めれば特異点の周りを一周する積分が簡単に実行できるというので,ローラン展開の技法を修得することに力を注いだわけだが,それ以外に留数を求める方法はないだろうか？
前回の具体例で,ローラン展開の主要部の項が有限個で終わることも,無限に続くことがあるのも見てきた.同じ関数であっても,どの点を中心に展開するかによって主要部の項の数は変わるのだった.主要部の分母の次数が最大
次までで終わる時,その特異点のことを「
位の極」と呼ぶ.無限に続くときには「真性特異点」と呼ぶのである.
1 位の極
の周りでのローラン展開は次の形になっている.
ここから留数
だけを取り出すにはどうしたら良いだろうか.この式の両辺に
を掛けてやろう.
右辺の最初の項は留数そのものだ.あとは簡単だ.この
を
に近づけたら右辺がどうなるかを考えてみたらいい.残るのは留数だけである.要するに関数
にを掛けて,その結果に対してをに近付けてやればいいのである.これをまとめれば次のようになる.
特異点が 2 位の極である場合にはどうしたらいいだろう？先ほどのように簡単ではない.なぜなら,ローラン展開は次のようになっているからである.
この両辺にを掛ければ右辺の第 2 項は留数そのものになるが,第 1 項が残っているためにをに近付けられないのである.そこで両辺に
を掛けて第 1 項を定数にしてやることにする.
そしてこれをで 1 階微分してやれば,第 1 項が消えるばかりか,第 2 項も留数そのものになる.
あとはさっきと同じようにをに近付けてやれば留数を残して全て消えてくれる.まとめれば次の通りである.
同じ調子でやれば何位の極でも同じことができそうだが,微分するたびに係数が増えてゆくので,それを消してやらないといけない.一般化すると次のようになる.
我々は関数を見れば特異点がどこにあるかを簡単に見つけることができるし,ローラン展開に慣れてくれば,その特異点が何位の極であるかというのも計算せずに判断できるようになる.こちらの公式に頼った方が楽だという場合にはわざわざローラン展開をしなくてもいいのである.特に 1 位の極の留数を求める公式はとても手軽であるから頻繁に使われる.
留数定理
我々はこうして,特異点の周りを一周する積分については簡単に計算できるようになった.留数さえ導ければ次の公式で結果を出すことが出来るのである.
簡単な関数の場合には眼力だけで答を出すことも可能だろう.
しかしこれは一つの特異点の周りを回った場合の話だ.内部に複数の特異点を含むようなコースで一周積分をしたときにはどうしたら良いだろう？その為の考え方はすでに次のような図を使って説明したことがある.
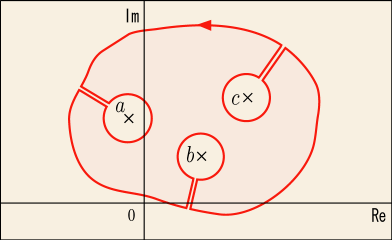
この図ではコースの内部に特異点を含んでいないので全体の積分は 0 である.一番外側の反時計回りの大きな円形コースと,それぞれの特異点の周りだけを「時計回り」に回るコースの合計が 0 なのだから,外側の円形コースの積分は,それぞれの特異点の周りの「反時計回り」のコースの積分の合計に等しいことになる.
要するに複数の特異点を含むコースでの積分を計算したければ,それぞれの特異点の周りについて求めた留数を合計すればいいということである.
この簡単な話が「留数定理」と呼ばれるものだ.
言い残したことはなかったか
以上で複素積分をする上で必要になることをほとんど説明し終えたと思う.何か説明しないままになっている問題が残っていなかっただろうか？
そう言えば,以前,不定積分のような計算方法がいつでも使えるかどうかについて議論したことがある.ここまで理解すればそれについての事情も分かってもらえるのではないだろうか.ローラン展開した時に留数が 0 にならないような特異点がある場合,始点と終点を固定しただけでは積分値が決まらないのである.なぜなら積分経路が特異点の周りを一周するたびに値が変わるからである.その辺りを把握して気を付けながら使うなら,不定積分のような計算を利用することもできるだろう.
あとは,ワイエルシュトラスの定理というものを軽く説明しておいた方が良いかも知れない.これは,真性特異点ならばそこに近付くやり方によって関数の値をどんな値にでも収束させられる,あるいは発散させることさえもできるというものである.その証明には,ローラン展開した時の主要部の項が無限にあることを使う.
以前に真性特異点の説明をした時には「近付く方向によって収束する関数の値が異なる」ものだと定義し,今回は「ローラン展開した時の主要部の項が無限に続く」のが真性特異点だと説明したが,二つの異なる説明が実は同じものを指しているのだと保証してくれているのがこの定理である.実用上はこれくらいの知識で十分なので,この定理の証明は他の教科書に任せることにしよう.
