物理数学：SU(3)

エルミート行列の方から攻める

さていよいよこれから SU(3) について考えていこう.これは普通の人にとってほとんど未知の領域であろう.SO(3) の場合には,その生成子の組み合わせが織りなす性質はとても不思議なものだったが,群そのものは 3 次元の回転としてイメージすることが出来た.しかし SU(3) は簡単にイメージできる対応物がなさそうだ.

SU(3) とは,行列式を 1 に制限した 3 次元のユニタリ行列であり,その自由度は 8 個あるというのは最初の方で確かめた.しかしその全ての自由度を含んだ形で具体的に書こうとするとおそらくとても複雑である.SO(3) でさえ,自由度は 3 つしかないが,それをやろうとすれば相当に複雑な形になるのだ.

3 次元の回転を一般的に表す方法は幾つかあるが,オイラー角というものが有名である.例えば x 軸の回りに θ₁ だけ回し,次に y 軸の周りに θ₂ だけ回し,最後にもう一度 x 軸の周りに θ₃ だけ回すという方法で,あらゆる姿勢への変換を表すことができる.これは言うだけなら簡単ですっきりしているが,つまりは,3 つの回転行列を掛け合わせてできる複雑な行列が,3 つの自由度を含んだ一般的な形だということになるだろう.

こういうことを考えるのはあまりに面倒なので,ユニタリ行列が $U=e^{iH}$ という形に表せることを利用して,行列の方に注目することにする.はエルミート行列なので,対角成分が実数で,対角成分を挟んで対称な位置には複素共役になっている.またの行列式が 1 であるという条件はの対角和が 0 になることで実現できる.それで次のような a～h の 8 つの自由な実数を使って表せるだろう. このは次のように 8 つの行列に分解して表すことができる. この 8 つの行列が SU(3) の生成子である.これからこれらの性質を調べていくためには一つ一つに名前を付けてやる必要があるだろう.名前を付けるというのは大げさで,ただ,それぞれを区別するための番号を振るだけでいい.しかし適当に番号を振っていいものだろうか？調べていくうちに,「初めにもっと番号付けに気をつけていればそれぞれの関係をすっきりした式でまとめられたのに！」と後悔することになるかもしれない.

さらにもう一つの心配は,ここに書いた 8 つの生成子以外にももう少し別の表現が許されている点だ.どれか,あるいは全部を定数倍してもいいだろう.符号を変えてもいい.それにの対角和を 0 にするには他のやり方もあったはずだ.

誰もが納得の行くようなスマートな表現方法や番号付けの方法なんてものがあるだろうか？

ゲルマン行列

いきなりスマートな例を示してしまって注釈を加えていく方が説明が楽だろう.SU(3) の対称性は物理学では素粒子論に関連している.次の表現はクォーク模型の提唱者であるマレー・ゲルマン(Murray Gell-Mann)にちなんでゲルマン行列と呼ばれる. 先ほどのものとはかなり順序が変わっているし,虚数が含まれるものは符号も変わっている.それだけではなく対角行列である λ_3 と λ_8 は中身も先ほどとは違ったものが採用されている.このようにしても対角和が 0 になるのはすぐに分かるだろう. λ_8 には奇妙な定数も掛けてあるし,中身も相当に奇妙である.

この番号付けと 3 列ごとに分けた並べ方にはある程度の意味がある.まず,最初の λ_1 , λ_2 , λ_3 に注目しよう.これらの左上 4 成分を眺めると,これは SU(2) のところに出て来たパウリ行列と同じ形になっている. そのため,これら 3 つの行列についてはパウリ行列のときと全く同じ,次のような関係が成り立っている. λ_1 , λ_2 , λ_3 だけを使う限りは,群の構造は SU(2) と同じになっていて,この 3 つの生成子で表せる範囲を飛び出さないのである.つまり,これらだけを使って $e^{iH}$ を作れば,それは部分群になっている.このように,ある程度理解できているものに似せてやった方が構造を把握するための負担が減らせそうだ.

λ_4 と λ_5 は,その行列成分の 2 行目と2 列目を隠してやれば,やはりパウリ行列の σ_1 と σ_2 と同じになっている.だとしたら,もう一つの行列を λ_8 のようにしないで, というものを採用してやれば,これらの間にもパウリ行列と同じ交換関係が作れたのではないだろうか？しかしそれは敢えてやらなかったのである.この行列は λ_3 と λ_8 を組み合わせて 1/2 λ_3 + (√3 )/2 λ_8 としてやれば作ってやることができる.

同様に λ_6 と λ_7 の行列成分の 1 行目と1 列目を隠してやれば,やはりパウリ行列の σ_1 と σ_2 と同じになっているので, という行列があればパウリ行列と同じ交換関係が作れたはずだが,これも採用しなかった.ちなみにこちらは, - 1/2 λ_3 + (√3 )/2 λ_8 としてやれば作ってやることができる.

なぜ λ_8 をわざわざこんな形に定めたのかについての説明はもうしばらく待ってもらおう.

λ_1 , λ_2 , λ_3 の間の交換関係はもう明らかになったが,我々は 8 つの生成子の交換関係を全通り試してみなくてはならないだろう.そして次の形に合うように構造定数 $f_{abc}$ を決定してやるわけだ. 実際に試してみる組み合わせはそれほど多くはない.とが同じなら左辺は 0 になるので,添字の部分が $f_{aac}$ という形のものは試すまでもなく 0 になるだろうし,とを入れ替えた場合には $f_{abc}=-f_{bac}$ となるのでこれも試す必要はない.左辺を 28 通りほど計算して,その結果を右辺の形に合うように分解してやれば $f_{abc}$ が求まる.

しかし実際にやってみろと言われれば,ちょっと逃げ出したくもなる.ゲルマン行列という,ある意味「完成した形」を知らない段階では特にそうだ.自分でとりあえず仮に作ってみた生成子を使って気軽に試してみようという気にはなかなかなれない.我々はなるべく手間を減らしたいし,できるものなら $f_{abc}$ のほとんどが 0 であってくれるとありがたい.パウリ行列の場合は $f_{abc}$ の添字のそれぞれに 1～3 が入って組み合わせは 27 通りあるが, $f_{abc}$ のほとんどが 0 であってくれるお陰で,和の記号を使わないようなシンプルな式で交換関係が表せているのである.

ここで「行列の規格直交化」という,他では聞かないアイデアを導入しよう. 「二つの異なる行列の積の対角和は 0 になって,同じ行列どうしの積の場合だけは対角和が 0 にならない」という条件である.試してみると,既に挙げたほとんどの行列でこれが初めから成り立っている.右辺に 2 が入っているのは,ほとんどの行列で自分自身どうしの積の対角和が 2 になるので,こうしておけばほとんどの行列はそのまま変更する必要がないからである.

実は初めに用意した方の 8 つの生成子のうち,対角行列になっているものどうしだけがこの条件を満たせない.この条件を満たせるように変更を加えたのが,ゲルマン行列の λ_8 なのだ. λ_8 の奇妙な形の謎がこれで少し解けた.しかしなぜ (2) 式のような条件を課す必要があったのだろうか？

それを説明しよう.まず記号の混乱を避けるために,(1) 式の右辺の和を表す添字を変えたものを用意する. そしてこの両辺に右からいずれかの行列 λ_c を掛けて,全体の対角和を計算してみよう. ここで (2) 式の条件を使えば右辺はとても簡単になり,次のようになる. この左辺を対角和の性質（行列の積の順序をリング状に入れ替えてもいい）を使って変形していくと, となるので,結局, であることが言える.構造定数 $f_{abc}$ は最初の 2 つの添字を入れ替えても符号が反転するし,今では 1 番目と 3 番目の添字を入れ替えても符号が反転することが分かった.この二つの結果を組み合わせればどの 2 つの添字を入れ替えても符号が反転することが言える.すなわち $f_{abc}$ は「完全反対称」であると言える.もちろんこれは (2) 式の条件があってこそ成り立つ性質だ.

これにより $f_{abc}$ は大幅に制限を受けることになる.もし 3 つの添字のどこでも同じ数字が入っていれば,それらを入れ替えても同じ数値であり,かつ符号が変わらなければならないので,それは 0 でしかあり得ない.3 つの添字がそれぞれ異なるものだけを調べればいいことになる.しかも,3 つの添字の順序を変えたものは符号が異なるだけであるから,順序が異なるものをいちいち調べる必要もない.それでも 8 つの中から 3 つを選んでくる組み合わせは 56 通りあるのでまだまだ多い気がする.実際はもっと簡単だ.やってみよう.そうすれば分かる.

構造定数を調べ上げる

とりあえず [λ_1, λ_2] を計算してみる.これは先ほども説明した通り,パウリ行列と同じ結果になるから 2iλ_3 になる.すなわち, $f_{123}=2$ であることが分かる.この時点で $f_{124}$ , $f_{125}$ , $f_{126}$ , $f_{127}$ , $f_{128}$ も 0 だということが分かる.

次に [λ_1, λ_3] を計算してみるが,これもパウリ行列の計算で結果が分かっていて, -2iλ_2 になるだろう.つまり $f_{132}=-2$ であるが,これは計算しなくても先ほどの結果からすでに分かっていた.ただ,このことによって $f_{134}$ , $f_{135}$ , $f_{136}$ , $f_{137}$ , $f_{138}$ も 0 だということが分かる.

こんな調子で潰していくと,意外とサクサクと確認が進む.それで結局は,次のような組み合わせだけが値を持つことが分かる. 添字を入れ替えたものは省かせてもらった.

ここまですっきり減らしてまとめることができたのはゲルマン行列の利点だ.あまり対称性の美しさを感じないかも知れないが,ここまでの話を思い出すと意外とイメージしやすい形になっている.

まず $f_{123}$ はパウリ行列と同じイメージだ.

λ_4 と λ_5 もパウリ行列と同じで, となっている.この最後のカッコ内は前に言ったように, という行列を意味しているのだった.

λ_6 と λ_7 も同じで, となっている.この最後のカッコ内も前に言ったように, という行列を意味しているのでパウリ行列と同じような内容になっているのだ.

他にも色んな絡み合いが表されているのだが,特に注目しておきたいのは,添字に 3 と 8 を同時に含んでいる $f_{abc}$ が見当たらないという点だ.それで,次のような関係になっていることが分かる. λ_3 と λ_8 は可換なのだ.つまり,一方の行列の固有ベクトルは,同時にもう一方の固有ベクトルになっている可能性がある. λ_3 と λ_8 はどちらも対角行列だから固有値は見ただけで分かるし,固有ベクトルは次のような 3 つである. これらのベクトルを |m,s>} という記号を使って表すことにしよう.が λ_3 の固有値で,が λ_8 の固有値を意味している. λ_3 の固有値は,,の 3 つで, λ_8 の固有値は 1/√3 , 1/√3 , -2/√3 の 3 つであるから,次のように表せる. 状況が分かりにくいので図示してみよう.

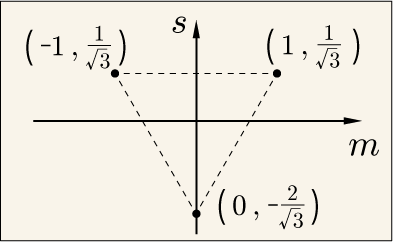
ゲルマン行列の可換な行列の固有値の組み合わせを図示してみたら三角形の頂点が描かれることになる説明図

3 つの固有ベクトルが,綺麗に正三角形の頂点に位置している.なぜこんなことが起きているのだろう？うまく出来過ぎのような気もする. λ_8 に付いている 1/√3 という係数がなければこうはならなかったはずなのだ.それでも三角形にはなっただろう.この係数は「行列の規格直交化」に従ったためであって,SU(3) の本質ではない気もする.しかし,この美しさは何なのだろう.

物理との関係

物理ではこの 3 つの直交するベクトルを,3 種のクォークだとみなして議論を進めることになる.現在ではクォークは 6 種類あることになっているが,初めにクォーク模型が提唱された時点では,アップ,ダウン,ストレンジの 3 種のクォークがあれば当時次々と見つかり始めた多数の素粒子を説明できると考えられたのである.

興味深い話ではあるが,残念ながら今回の話だけではまだそのような初期のクォーク模型の話すら進められない.3 つの反クォークを導入しなくてはならないし,さらにクォークの組み合わせを議論する方法を学ばなくてはならない.

それは角運動量の合成の話に非常によく似ている.角運動量を持つ複数の粒子が集まった時に,全体としてどのような角運動量の状態を取りうるかという話であり,SO(3) や SU(2) でやった「直積表現と既約分解」がそれにあたるのだった.SU(3) でもそのようなことを考えなくてはならない.

3 つのベクトルがそれぞれ 3 種のクォークに対応すると言われても,唐突すぎてイメージが難しいかも知れない.これには参考になる前段階の理論が存在している.SU(2) の構造が素粒子のスピンに対応していることはすでに紹介したが,スピンと全く同じ理論体系を使って素粒子を分類できると考えたのである.この考えを「アイソスピン」と呼ぶ.

例えば,陽子と中性子はお互いに質量が非常によく似た粒子である.スピン上向きの電子とスピン下向きの電子が,スピンが異なるだけの同種粒子であるように,陽子と中性子も,アイソスピンが異なるだけの同種粒子なのではないか,と考えたのである.質量以外には色々と違って見えるが,わずかな性質の違いによって大きな差異がもたらされている機構が裏に隠されているだけあって,実際は状態がわずかに異なるだけなのだというのである.その状態の違いを,スピンと同じように,互いに直交するベクトルで表したわけだ.

このアイソスピンは通常のスピンのように合成系を考えることができて,中性子や陽子が多数集まって出来ている原子核の状態を説明できる.つまり,様々な核種の存在とその性質を説明するのに役立っている.

3 種のクォークをベクトルに対応させるのはこのような考えの自然な拡張であるわけだ.

数学との関係

話が物理に偏りすぎたので,SU(3) の数学での扱われ方も少し説明しておこう.それをしておかないと,読者が数学書にチャレンジするときには全く違う学問を勉強している気分になってしまう.数学書は一般的に成り立つ法則を証明するのに夢中で,そこで語られている具体例を示して試してみるのは読者に委ねられているからである.

SU(2) や SO(3) では生成子の固有値はだけで表せて固有ベクトルを区別できるのだった.しかし今回の SU(3) ではとの二つが現れることになった.このようなやのことをリー群論の用語では「ウェイト」と呼ぶ.「重み」という意味だ.先ほど描いた三角形のような図は「ウェイト図」と呼ばれる.

SU(4),SU(5) と増えていくに従い,ウェイトの種類は増えていく.生成子の中に,可換なものが増えていくからである.相互に可換な生成子の最大数を「群のランク」だとか「リー代数の階数」だとか呼ぶ.SU(N) の階数は N-1 であることが証明できる.SU(3) の場合は 2 だから,ウェイト図は 2 次元平面で表せたのである.

今回は相互に可換な生成子は λ_3 と λ_8 だったが,このような可換な生成子の集まりのことを「カルタン部分代数」と呼ぶ.

SU(2) や SO(3) では $L_{+}$ や $L_{-}$ という行列を作って,ウェイトを上げたり下げたりしたのだった.SU(3) でもそのようなことが可能である.ただし,そのような働きを持つ行列は全部で 6 種類作られる.生成子の中でカルタン部分代数に含まれないものの数が 6 であり,それらの線形結合で作るわけだから,独立なものは 6 種類だというわけだ.

$L_{+}$ や $L_{-}$ はの値を 1 ずつ上げ下げしたが,SU(3) で同様なことをすると,との値を同時に変化させることになる.ちょうど,先ほどのウェイト図の三角形の辺の上を進む形になる.それぞれの辺の上を一方に進むものと,逆方向に進むもので,6 種類あるわけだ.

このようにウェイト図の上で進む向きはベクトルで表わされるので,これを「ルート・ベクトル」と呼ぶ.あるいは単に「ルート」とも呼ぶ.なぜルートなのか,私にはまだイメージがつかめないでいる.route だったら分からなくもないが,そうではなく root である.と同じだ.

次回はこの辺りを詳しく調べることにしよう.今回は生成子として 3 次の行列を使っていたが,SU(2) や SO(3) で 2l+1 次元表現が可能だったように,SU(3) でもこれとは別の次数の行列による表現が許されている可能性がある.構造定数 $f_{abc}$ を使って,生成子と同じ次数の行列が作れることは前に話した.そういうものを「随伴表現」と呼ぶのだった.少なくとも 8 次の行列による表現はできるだろうことは分かる.その場合のウェイト図はどのような形になるのであろうか.

係数についての注意書き

今回の記事で求めた構造定数 $f_{abc}$ の値は,多くの教科書に書かれているものの 2 倍になっている.習慣として,ゲルマン行列に 1/2 を掛けたものが生成子 T_i として用いられ, という関係になっており, という関係になるように $f_{abc}$ が決定されるからである.

このように定義するとウェイトの値は半分になり,ウェイト図の三角形の一辺の長さがちょうど 1 になるので少しだけ気持ちいい.物理でスピンを扱うときにもパウリ行列を 1/2 倍したスピン行列を使うので,同じような感覚に浸れるという利点がある.

今回の記事では天下り的な理由で不自然なことをしたくなかったので,敢えて習慣に従わずに計算を進めた.習慣に従ったやり方をすると,あちこちに 1/2 が現れて非常に面倒な印象になる.規格直交化の条件式である (2) 式の右辺にある 2 が消えてくれれば嬉しいが,ここにも 1/2 が現れるのである.