物理数学：収束、発散の判定法

級数の基本

数学の教科書ではないのだから,厳密さへの気配りはあまりしなくてもいいだろう.それよりも,この辺りの状況を素早く飲み込めることに力を注いでまとめたいと思う.おおよそ納得できる程度の軽い証明は入れていきたい.

早速始めよう.次のような形式で書かれる,無限の項から成る式を「級数」または「無限級数」と呼ぶ. 無限に足し合わせるのだから合計した値は無限になりそうなものだが,そうとは限らない.例えば次のようなものが分かりやすい. 図に表せば,この値が 1 に近付くのがはっきり理解できるだろう.

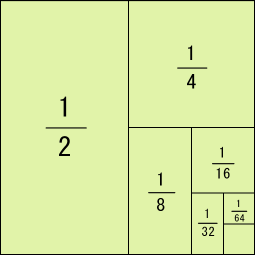
このように,無限の項からなる和が,ある一定値に限りなく近付く場合があり,それを「級数が収束する」と表現する.もちろんこの説明は数学の立場から見ればかなり曖昧なものである.

前回の説明の中で調和級数というものを紹介したのを思い出してみてほしい.今の例と同じように,加えられる項は徐々に小さくなって行き,限りなく 0 に近付くのであった.そこでは「無限に小さくなるものを加えていっても無限大に発散してしまうことの驚き」を書いた.しかし今回は「無限に加えていったものが無限に発散しないことが直感に反している」ような書き方をしている.まったく,どっちだったなら不思議じゃないというのか.人間の感覚など本当に勝手なものである.

ところで,数学の教科書を読むと「級数の和」という用語がわざわざ定義されている.まず,級数の有限の項までの和を S_n とおく. そして n→∞ に近づけたときにこの S_n が一定値に収束するようなら,その値 S_∞ を「級数の和」と定義するという二段構えのやり方だ.級数というのはそもそも和の形で表現されたもののことなのだから「級数」と「級数の和」は結局は同じものを表しているんじゃないのかと素人目には思えてしまう.しかし,数学では収束する先の値が存在するかどうかに気を使うことで,存在しないものについて議論してしまう過ちを厳しく防いでいるのである.この辺りからも数学はかなり慎重に論理を進めているのがうかがえる.

数学の論理の中に無限というものが持ち込まれて以来,こいつが誤った結論へと導く論理の落とし穴となっているのである.（それを避けるために数学では実に巧妙なやり方を発明しているのだが,それには触れないでおこう.）例えば次のようなことには特に気を付ける必要がある.

項が無限に続く場合には,和の順序を変えてはいけない！

なぜそれがいけないのか？いや,幾つかの数えられるくらいの項の順序を変えるくらいでは確かに問題は起こらないのだ.しかしそれを無制限に行うと結果が変わってしまうのである.最も単純な例は次のようなものだ. これは 1 と -1 とを交互に加えていくものであって,いつまでも一定値に収束しないのだから,実は考えない方がいいものだ.しかしカッコを付けることでこの計算順序を変えてしまうとどうなるか？ほう！ S=0 になると言えそうだ.しかし次のようにカッコを付けたらどうなるか. 今度は S=1 になるようにも思える.このようなトリックが幾らでも可能になるのである.

今の例は簡単すぎたから「大丈夫,自分はこの程度のことには引っかからない」と思うかもしれない.ではもう少しまともに見える例で説明しよう. この級数が収束してが値を持つためには少なくとも n→∞ で a_n →0 とならないといけない.なぜって,ずっと進んだ先で a_n が突然大きな値を持つようなことがいつまでも続くようなら,一定値に落ち着くように見えたの値が突然ガバッと変わる可能性がいつまでたっても拭えないわけで,の値が一定値に落ち着くはずがない. n→∞ で a_n →0 であればは必ずしも一定値に収束するとは言えないが,が収束するためには少なくともこの条件は満たしていないといけない.このことを前提とした上で,次のような項の入れ替え操作を考えてみよう.

まずテキトウに値を決める.そうだな,とりあえず 4 でいいや.そして無限に続く a_n の初めの方から順番に正の項だけを選んで足して行き,4 を超えた時点で今度は負の項ばかりを最初の方から順に選んで足してゆく.そうしてそこまでのの合計が 4 を下回ったら再び 4 以上に回復させるべく正の項の続きを足してゆく.4 を超えたら再び負の項の続きを・・・.そんなことを繰り返すうちに足したり引いたりする a_n の絶対値はどんどん小さくなってくるし,は 4 に収束すると言えるのではないだろうか？こんな感じの手続きによって,4 じゃなくてもどんな好きな値にでも収束させることができそうだ.

もちろん,このトリックはいつでもできるものではない.例えば正の項ばかりの級数だったならこんなことはできないのがすぐに分かるだろう.

すると,項の無限の入れ替えに関して,どんな場合にどんな危険があると言えるのだろうか？いつでも危険なのだろうか？安全な場合もあるのだろうか？詳しくは後でまとめよう.今はただ,危険な例があることを紹介したかっただけなのだ.深追いはしない.

項の順序を変えても問題ない場合もある

項の順序を入れ替えることを極端に恐れる必要もない.不安な場合には,順序を入れ替えても問題ないことを証明してやればいいのだ.有名なのは次のような例だ.

「数列 $\color{red}{\{a_n\} }$ と $\color{red}{\{b_n\} }$ の無限級数がどちらも収束するならば次の式が成り立つ」

これは,

のような形の無限級数があった場合に $\{a_n\}$ と $\{b_n\}$ の無限級数がどちらも収束する場合に限って,計算順序の変更操作をして,それぞれを別々に分けて計算してから後で加えるようなことをしても問題ないことを意味している.

＜証明＞

証明といっても数学のように厳密にはしないし,必要最小限の最短ルートで進むつもりもない.軽く納得できる程度のイメージを説明して終わろう.

これは大した話でもない.計算の順序を変える操作を無限回行っているのは確かだが, $\{a_n\}$ や $\{b_n\}$ をそれぞれに分けて見た時,その中の並びまで変えることはしていないのだから話は簡単なのである.とりあえず有限項までの和を考えれば,それは「それぞれの有限項までの和」を二つ合わせたものとして単純に表せる. このように書き換えて良いのは,項の数が有限である場合には計算の順序を変えることには全く問題がないからである.この項の数を増やして行き,無限にまで近付けて行っても式はずっと同じ形のままであろう.今回はこの右辺のそれぞれの値の行き着く先はちゃんと分かっており,そこへ収束すると言えるわけだ.

交項級数

正の値の項と負の値の項が交互に続く級数を「交項級数」または「交代級数」と呼ぶ. なぜこの形の級数にわざわざ名前を付けるほどに重要かというと,色んな場面でこの形の級数がたびたび登場する上に,次のような分かりやすい定理が成り立っているからである.

「 $\color{red}{a_n }$ が単調減少で 0 に収束するならば,交項級数は収束する」

＜証明＞

これは図を描いてみれば状況がすぐに把握できる.項が増えるごとに和がどう変化するかを想像してみよう.最初の項が一番大きくて,次の項でそこからかなり引くことになるが,最初の項よりは小さいのでまだ正の値である.次の項で再び揺り戻すことになるが最初の水準には戻れず,次の項でまた減るが減り方も先ほどより少ない.要するに,振動の幅を減らしながら進むイメージなわけで,必ずどこかにたどり着くことになる.以上だ.数学用語を使って厳密に証明したい人は数学の教科書を参考にしてほしい.

絶対収束

次のような級数があるとする.まぁ,普通の級数だ. この級数の各項の絶対値をとって作った次のような級数を考える. この (2) 式の形にしても級数の和が収束することを,「(1) 式は絶対収束する」と言い表す.

負の項が含まれないようにして一方的に増加するようにしても収束するのだから,絶対収束というのは普通の収束よりも難しい条件をクリアしているのである.そこで次のことが言える.

「級数が絶対収束するならば,級数は収束する」

＜証明＞

まず,元の級数の各項を二種類に分類して次のように表す. ここで使っている $a^{+}_n$ と $a^{-}_n$ の定義を見ればこの式に納得できるだろう.それはそれぞれ次の通りである. こう定義すれば $a^{+}_n$ も $a^{-}_n$ も常に正である.さらに, $a^{+}_n$ も $a^{-}_n$ も常に |a_n| 以下である.このことから, $a^{+}_n$ も $a^{-}_n$ もそれぞれ独自に無限級数を計算すれば収束すると言えるのである.なぜなら,各項が常に正であるので増加する一方のはずだが,それより常に値が大きな |a_n| の級数でさえも収束するのだから,それ以下の値にとどまるに決まってるというわけだ.それで,(3) 式はつい少し前に出てきた話を当てはめることで,次のように表して良いことになる. この右辺はちゃんと値を持つので, a_n の無限級数は収束すると言えるのである.

条件収束

たった今,絶対収束するなら級数は収束するということを説明したが,その逆は言えない.絶対収束しない場合については,収束することもあれば収束しないこともある.絶対収束しない級数が収束することを「条件収束」と呼ぶ.

ところで,最初の方で,「無限級数では項の無限回の入れ替えをすると結果が変わってしまうので気を付けるべき」という話をしたのだったが,気を付けるべきなのは,この,条件収束の場合だけだ.なぜなら,絶対収束する場合には項の入れ替えをしても結果が変わらないことを示すことができるからである.その証明はしないつもりだったが,気になる人もいるだろうから別ページで説明しよう.

絶対収束する級数と条件収束する級数の違いをもっと分かりやすくイメージしてみたい.そのためにこんなことを考えてみる.まず,条件収束する級数を考えると,その中には負になる項が必ずあるに違いない.なぜなら,全ての項が正であるようなものが収束するなら,それは絶対収束と何ら変わらないからだ.そこでひとまず「絶対収束する場合も条件収束する場合にも負の項は含まれることはあるが,条件収束する場合には必ず負の項が含まれる」と言えるだろう.というわけで,正の項 p_n と負の項 -q_n を分けて,次のように表してみよう. こんな風に表して良いかどうかは,右辺の第 1 項と第 2 項がどちらもちゃんと収束してくれるかどうかに掛かっている.もしどちらも収束してくれるとすれば,ここでは p_i も q_j も正の値なのだから,絶対値を付けても収束してくれるに違いない.つまり,この式が表しているのは絶対収束だということになる.

すると条件収束というのは,この右辺のいずれかの項が発散してしまう状況だと言えるわけだ.しかし一方の項が収束してもう一方が発散するのでは,一方が他方に負けて全体が発散してしまうことになるだろう.だから条件収束というのは,この右辺のどちらもが発散しているような状況であり,正の項と負の項の微妙なバランスでもって全体が収束に向かうような状況だと言えるわけだ.

もう一度まとめよう.「条件収束とは,正の項と負の項がそれぞれ独自には発散してしまうほど存在しているのに,互いに何とかして打ち消し合っている状況である.」ここで最初の方の「無限級数では項の無限回の入れ替えをすると結果が変わってしまうので気を付けるべき」という話をもう一度思い出してもらいたい.そこでは「項の順序を変えることでどんな値にでも収束させてしまえるトリック」を紹介したのだった.条件収束の場合にはそれがいつでも使えてしまうのではないだろうか.それほどまでに,条件収束での順序の入れ替えは危ういということだ.

しかし「条件収束の場合にはどんな項の入れ替えも許されない」というわけではないのはすでに確認した通りだ.安全性が証明されているような順序の交換の仕方を使う分には問題はないのである.

収束判定法　その 1

無限級数が収束するのか発散するのかについて調べる簡単な方法がある.「ダランベールの比判定法（比テスト）」と呼ばれるものだ.まず,次のような計算をして値を求める. α>1 なら無限級数は発散する. α<1 なら絶対収束する.ちょうど α=1 になる場合にはどちらとも言えない.絶対収束する場合もあるし,条件収束する場合もあるし,発散する場合もある.そういう場合は何とかして別の方法で調べる必要がある.

＜証明＞

まずは α>1 の場合を考える.これはが増えていくに従い $|a_{n+1}|/|a_n|$ の値が必ずどこかで 1 を超える,あるいは最初から超えていたことを意味する.要するにあるところより先ではずっと $|a_{n+1}| > |a_n|$ であり, |a_n| は増大する一方である.よって級数は発散すると言える.

次に α<1 になる場合について考えよう. α<β<1 となる値を用意する.そうするとを増やしていく過程で $|a_{n+1}|/|a_n|$ の値が必ずどこかでを下回って,それきりずっと戻ってこないところがあるはずだ.それを番目の項だとしよう.番目以降の a_n の絶対値は次のように表せる. これを使って番目以降の級数を書いてみるとであり,右辺の $(|a_N| β^{-N})$ は有限の定数値だし,右辺は公比 β<1 の等比級数であることが分かる.つまり右辺は収束するわけだ.左辺の各項は常に正であり増える一方でありながら結局は右辺より小さく抑えられているので,左辺は発散するはずがなく,つまり収束することが言える.第項より前の項の和は有限の値なので,結局和の範囲を広げて $Σ_{n=1}^{∞}|a_n|$ としたものも収束することが言えているのである.これは a_n の級数が絶対収束することを表している形ではないか.

さて,残る α=1 の場合については特に言うことがない.だから何も言えないのである.

冪級数

さあ,ようやく本題に近付いてきた.次のような形の級数を「冪級数」と呼ぶ. これを和の記号を使って短く表せば次のようになる. このような級数は変数の値によって収束するかも知れないし,発散するかも知れない.実はそれに関して次のような定理が成り立っているのである.

「冪級数が $\color{red}{x=c}$ で収束するならば, $\color{red}{|x|<|c|}$ で絶対収束する」

いきなりそんなことを言われても何のことかさっぱり分からないかもしれない.つまり,正でも負でもいいから何らかの値をに代入して計算した冪級数がたまたま収束していることを発見したら,絶対値がより小さいなら,どんな値を代入しても収束するというのである.しかもそれがただの収束ではなく絶対収束だというのだ.

＜証明＞

和が収束するのだから,項の値はどんどん小さくなって行っているはずだ.つまり n→∞ で $a_{n}c^n →0$ に向かっているはずだ.それで常に $|a_{n}c^n| ≦M$ となるを決めることができる.この関係を使えば,次の式が作れる. これを級数の形にしてみても次の大小関係が言える. ここでもし |x|<|c| ならば,この右辺は公比が |x/c|<1 の等比級数であり,収束することが言える.すると,左辺の級数の各項は常に正でありながら右辺で発散が抑えられていることになるので,収束すると言える.左辺をよく見れば,この形のものが収束するということは絶対収束の条件を満たしていることになるではないか.

収束半径

今説明した定理はとても面白いことを表している.原点からある距離だけ離れたところの値をに代入した時に収束することが分かれば,それよりも原点に近い点では全て絶対収束するのである.どこか遠くで一点でも収束することが分かれば,その距離の内側ですべて絶対収束する.

つまり,収束するかしないかの境目はそう幾つもありはしない.三つの場合がある.どんなを代入しても収束するか,0 以外のどんな値を代入しても発散してしまうか,どこか原点からある距離のところで境目が見出されるか,これらのいずれかである.この境目までの距離のことを「収束半径」と呼ぶ.

どんなを代入しても収束する場合,「収束半径は無限大である」と表現する. x=0 以外のどんな値を入れても発散する時,「収束半径は 0 である」と表現する.

そう言えば,ひとつ気をつけることがある.この定理が保証しているのは収束半径より内側についてだけである. x=c で収束したからといって,原点を挟んでちょうど反対側にある x=-c の点でも収束する,とまでは言えないのである.それは実際に「場合によりけり」である.その点で収束するか発散するかはその都度調べてみないと分からないことである.

いや,もう少し正確に言っておかないといけない.実は,収束半径がであるとき, x=r と x=-r のどちらでも発散する場合というのもあるのである.

冪級数をずらす

ここまでの冪級数の話は,の原点をずらしても成り立っている.例えば $x_{0}$ だけずらしてやると次のような形になる. テイラー展開と同じ形だ.この式で $x=x_{0}$ を代入すると,上の話での x=0 と同じことになる.この式を和の記号を使って短く表せば次のようになる. 定理は次のように言い換えればいいことになる.

「冪級数が $\color{red}{x=c}$ で収束するならば, $\color{red}{|x-x_{0}|<|c-x_{0}|}$ を満たす $\color{red}x$ で絶対収束する」

$X=x-x_{0}$ とでも置けば上と同じ話なので,わざわざ証明し直す必要もないだろう.ここまでの話は同じように成り立つから,収束半径というのは $x_{0}$ からの距離を表すことになる.

収束半径を求める方法

いよいよ本題である.テイラー展開がどの範囲で収束するかを知りたいのだった.つまり,今回の話に出てきた収束半径を求める方法が分かれば,テイラー展開がどの範囲で使えるかという判定にも応用が利くのである.

収束半径を求める方法で有名なのが 3 種類ほどある.手軽な順に証明なしで紹介しよう.

まずは「ダランベールの方法」と呼ばれるものだ.上で紹介した「ダランベールの比判定法」を応用したものである.(4) 式または (5) 式のような冪級数の収束半径は次の計算で求めることができる. しかし, a_n の形が少し複雑になってくるとこれが簡単に計算出来なかったりする. a_n に乗の形が含まれている場合などには次の「コーシー・アダマールの方法」の方が役に立つ. 見た目はちょっと難しそうだが,やってみるとどうってことない.解説が要らないほどの単純な計算だ.これでもうまく行かない場合は最後の手段で「コーシー・アダマールの定理」を使う. ここに出てくる $\limsup$ というのは「上極限」と呼ばれる数学の概念で,少し説明が要るだろう.正確に説明しようとすればかなり長くなるが,今回のような使用法に限れば大雑把に次のように言ってもいいのではなかろうか. $[1]{|a_{1}|} , [2]{|a_{2}|} , … , [n]{|a_{n}|} , …$ と無限に続く数列の番目よりも後にあるものの中で一番大きい値を考える.そのを無限大に向かわせた時にその「最大値」は徐々に下がって行くことになるわけだが,それが結局はどこへ落ち着くのか,というものである.

これは $[n]{|a_{n}|}$ が単純に単調減少するような場合には先ほどの「コーシー・アダマールの方法」とまったく変わらないことを言っているだけなのだが, $[n]{|a_{n}|}$ がいつまでも振動して極限が定まらない時にはこちらの考えを使う必要がある.収束半径が必ず求まる方法ではあるが,判定には手間がかかる.しかし考え方は何も難しくなかろう？

収束判定法　その 2

今紹介した収束半径を導く方法は無限級数が収束するかどうかの判定にも応用できる.なぜなら (4) 式のに 1 を代入したものはもう冪級数ではなく,(1) 式のようなただの無限級数の形になるではないか.

勘のいい人はこれだけでもう分かっただろう.つまりこういうことだ.(4) 式の収束半径を求めるつもりで「コーシー・アダマールの方法」なんかを使ってを導いてやり,もし r>1 だったならば (4) 式のに 1 を代入した形の級数が収束半径の内側にあることになるのだから,つまり (1) 式の形の級数は絶対収束すると言えるわけだ. r<1 ならば発散するだろうし,ちょうど r=1 の場合には何とも結論を下すことはできない.