カルノーサイクルの拡張
カルノーサイクルでは二つの熱源のみを考えて,
という関係があることを導いた.これは次のように変形することも出来る.
この式を,二つ以上の熱源がある場合に拡張しよう.
二つしか熱源がない場合にはが高熱源から受ける熱,
が低熱源に捨てる熱だとしていたが,複数の熱源がある場合にはどの熱源からもらってどの熱源に捨てることになるのか予め決める基準はない.そこで少し定義の方法を変えて,
番目の熱源からもらう熱を
と決めよう.よって熱を捨てる場合には負の値で示すことになる.また
番目の熱源の温度を
だとしておこう.
この表現の仕方を使うと,二つの熱源の場合の式は次のような表現に書き換わるだろう.
ここから類推するに,複数の熱源がある場合には次のような関係が成り立っているのではないだろうか.
これはあくまでも楽観的な予想ではあるが,実は本当にこの関係が成り立っていることをこれから示すことにしよう.
複数の熱源で動作する機関
複数の熱源からそれぞれ
を受けて仕事
を行うサイクル
を考える.
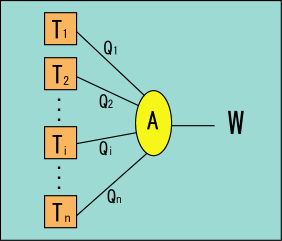
これは各熱源からもらった熱をすべて仕事に変えてしまうように見えるが,いくつかのは負になっているという想定であって,この図だけで捨てる熱も同時に表されていることになる.よって第 2 法則に反しているわけではない.
これは一つの装置を様々な熱源に次々と接触させて動作させるのを思い浮かべてもいいし,多数の熱源のうちのどれか 2 つの間で動作する幾つものカルノーサイクルがあって,それらがあたかも一つの装置であるかのように並列動作しているのを思い浮かべてもいい.前回,任意の準静的過程が多数のカルノーサイクルの集まりで表せるという話を図を使って説明したが,そのイメージがこれに相当する.
任意の準静的過程を表すためにはもっと無限に細かく分割する必要があるが,その状況については少し後で拡張しよう.
さて,これだけをいくら眺めていても望む関係式を導くことは出来ない.前回求めたカルノーサイクルについての結果を拡張したいのだから,それを使えるような別の状況を準備して,それと今回の状況とを関連付けることを考えてみよう.
例えば全く別の熱源を準備して,そこから熱を受けて動作するようなさっきとは全く別の多数のカルノーサイクル
を考える.
はそれぞれ熱源
から熱
を受けて仕事
をし,残りの熱
を熱源
に捨てる動作をする.
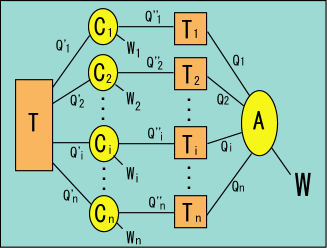
の内の幾つかは逆サイクルになっていて,外部から仕事をされて熱源
から熱を受け取り,熱源
に熱を返す動作をするものもあるかも知れないが,これらは全て
,
,
の正負の違いで表されているとしよう.こうすれば次のような多数の関係式を得ることが出来るだろう.
これらを全て足し合わせれば次の関係が得られる.
これと先ほどのサイクル
とを関連付けるためには,
という条件を付けてやればいい.これはサイクル
が各熱源から得た熱,各熱源に与えた熱を,
群を使って全て元通りに戻すという意味だと考えることも出来る.それが出来れば次の関係式が得られることになるだろう.
しかし果たしてそんなことは可能だろうか.実現不可能な状況を無理やり式にして喜んでいても,そんな式にはまるで意味がない.実際,サイクル
と サイクル
と熱源
を一つの装置だと見て内部を隠してしまうと少々おかしな所がある.
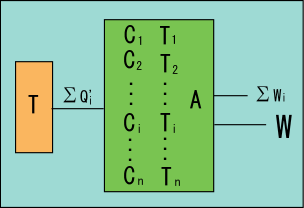
熱源から熱
を受けて全てを仕事
と
に変えたことになってしまっている.これでは熱力学の第 2 法則に抵触してしまうではないか.
しかし逆なら大丈夫だ.外部から仕事をすることでその全てを熱として熱源に戻すことはまるで問題ない.つまり
ならそれは許される状況だということになる.ただしこれは不可逆過程である.
は全て可逆サイクルなので,サイクル
に不可逆な過程が含まれていると考えるより他にない.恐らく熱源
の熱が仕事
に有効に変換されないまま別の熱源に漏れてしまうといったような不可逆な現象が内部で起きているのだろう.
つまり,サイクルが不可逆過程を含むときには
が成り立つということである.
ではサイクルが可逆だった場合はどうなるだろうか.この装置全体が可逆的な動作をするはずだ.よって
でなければならない.
は別に 0 になっていなくてもいいが,
と釣り合って全体として 0 でなければならない.可逆機関は外部に影響を残してはいけないのだ.つまり,
だということである.
カルノーの原理
以上で望むものが得られた.複数の熱源を持つサイクルについて,
が成り立つことが分かった.しかも不可逆過程を含むような場合についても考慮に入っている.望んだ以上の結果が得られたわけだ.これを「クラウジウスの不等式」と呼ぶ.
この結果を再び熱源が二つのみの場合に当てはめるなら,
だということになる.これを使って再び熱効率を計算してやれば,
となる.つまり,不可逆過程を含むサイクルの熱効率は,前回計算したよりも必ず低くなることが分かる.カルノーサイクル以上の効率を持つ熱機関は作れないのだ.このことを「カルノーの原理」という.
カルノー氏は 36 歳の若さで亡くなった.彼のこの天才的な考察は 20 年以上の長い間,歴史の中に埋もれてしまっていた.それを天才ケルビン卿が再び掘り起こしてようやく注目を浴びることになったのである.それを現在の形に分かりやすくまとめ上げたのはクラウジウス氏である.
新しい状態量
どんな形のサイクルにでも当てはめられるように上の話を拡張しよう.わずかに温度の異なる無限に多くの熱源を考えれば,それは連続的に状態が変化するようなサイクルと同じである.
つまり,気体の状態がいろいろに変化して最終的に元の状態に戻ってくる時,次のような不等式が成り立っていることになる.
これも「クラウジウスの不等式」と呼ばれている.積分記号に丸がついているのは,ぐるりと一周まわって積分することを意味している.等号は状態変化が準静的である時に成り立つことになる.
にはこれが不完全微分であったことを思い出すためにダッシュを付けてある.温度
の値は定数ではなく,積分の経路の途中で様々に変化する.
拡張はこれだけで終わりである.しかしこれは重要な結論を引き出すための始まりでもある.そのために,状態量と呼ばれるものの資格を思い出してもらいたい.どんな変化を経ようとも,気体の状態が同じである時にはいつも同じ値を取るものが状態量と呼ばれるのであった.今,微小量として
というものを考えると,
を積分しながら元のところへ帰ってくると……もちろん準静的過程を守る限りにおいてだが……その値が 0 になるというのが上での結論である.つまり一周した時の変位が道筋に関わらず 0 だということだ.すると,ある地点を基準にして
を任意の状態まで積分することで,それぞれの地点で値
が定義できて,その量
は同じ地点ではいつも同じ値になるのではないだろうか.
新しい状態量の発見である!これを「エントロピー」と名付けよう.語源はエネルギーの場合とよく似ていて,「en」がギリシャ語で「中へ」を表す接頭辞,「trope」がギリシャ語で「変化,変換」を意味する.クラウジウス氏による命名である.
カルノー氏もそのような量が存在するとの考えには到達していたらしい.多くの……しかし全体から見れば余りに少数の天才たちによって理論が作り上げられていったことが分かる.
次回はこの新しい状態量の性質を調べることにしよう.
修正履歴
(2004/09/14)
工事中の表示を解除.
(2023/11/26)
読みやすくなるようにわずかに修正.式変形の過程や積分中のTについての説明を追加した.










