熱力学：2 相平衡

蒸発について考える

密閉容器に 1 種類の分子だけからなる純粋な液体と,同じ分子からなる気体を入れて,2 つの相が共存するようにする.わざわざ液体と気体を別々に入れる必要はない.真空容器に液体を注ぐだけで,液体の一部はすぐに蒸発して真空は気体で満たされるようになるだろう.この液体はどこまでも蒸発を続けるわけではなく,ある程度蒸発したところで安定するのだが,なぜそこで安定するのだろうか.また,どんな条件で安定するのだろうか.それを探ろうというのが今回のテーマである.

密閉容器に水を少量入れておいて真空ポンプで空気を抜いてやると,熱くも無いのに水が勝手に沸騰するという実験を見たことがあるだろうか.また,高い山に登ると水が低い温度で沸騰してしまってそれ以上温度が上がらないので,煮え切らない料理が出来てしまうことは聞いたことがあるだろう.それを防ぐためには圧力釜を使って調理しないといけない.窓に勝手に水滴が付いたり蒸発したりとかいうのも良く見る.割と身の回りに起こる現象に近い話になってきた.

断熱条件での平衡

まずは前回と同じように体積の変化しない断熱容器を考えて,前回と同じ計算手法を適用しよう.容器全体のエントロピーが極大になるところで安定するのだった.

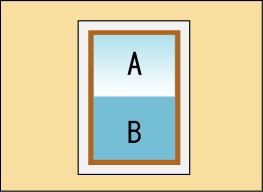
ところで,これまでの論理は気体に対して適用する事を前提にして進めてきたのであって,同じ概念をいきなり液体に対して用いてもいいのだろうかと不安に思うかも知れない.しかし液体にだって温度,圧力,体積がある.同じ論理が通用しないことがあるだろうか.そもそも気体と液体とは何が違うだろう.理想気体の性質から大きく掛け離れた気体の一種だと考えてはどうだろうか.

エントロピーを導入した時には理想気体の性質は何も使っていない.理想気体の性質から離れていたとしても,同じ論理が使えるはずである.よって液体についてもエントロピーの概念を同じように適用して計算しよう.容器の中の全体のエントロピーは次のように書けるとする. n_a と n_b は気体と液体を構成するそれぞれの分子のモル数である.分子はお互いに行き来して,ある時は気体に,ある時は液体になったりという具合に量が変化するので,それに応じてそれぞれのエントロピーも増減してしまう.そこで「1 モルあたりのエントロピー」というものを考えなくてはならない. S_a , S_b はそういう量である.

「1 モルあたりのエントロピー」という概念はここまで扱ってこなかった.何かこれを使う上で気を付けるべきことがあるだろうか.温度や圧力はモル数に関係ないのでこれまで通り使うしかない.しかし,体積やエネルギーはモル数に関係するので,これらについては「1 モルあたりの体積」や「1 モルあたりの内部エネルギー」などというものを考えて量を統一しておかなくてはならない.それさえしておけば各状態量の間に今までと全く同じ関係が成り立っているはずだ.つまり,ここで使った S_a( U_a, V_a ) という関数の中の変数 U_a , V_a というのは 1 モルあたりの内部エネルギー,1 モルあたりの体積を意味している.その事を頭に置きつつ,全エントロピーの 1 次の変分を計算してやろう. ところで今回の束縛条件は,「全体の分子数は変化しない」ことと,「全体の体積は変化しない」ことと,「断熱なので全体のエネルギーは変化しない」ことの 3 つである.式で書くと次の通りだ. このままでは使いにくいので,これらについても 1 次の変分を計算してやる. こうして出来た 3 つの条件を (1) 式に当てはめて力ずくで解けば解けないことも無いのだが,ここはラグランジュの未定乗数法を使う良い機会なので試してみるとしよう. と置けば, となる.この各項が 0 になるという条件により, という関係が簡単に導かれる.もう少しまとめれば, だということだ.これが「定積・断熱」条件における液相と気相の平衡条件である.こんな楽に求められるとは「未定乗数法」とは何とありがたい方法だろう.

さて,温度と圧力がそれぞれ等しいという条件については前回にも出てきたし,いかにもそうでなければならない気がする.温度差があれば熱エネルギーの移動があるし,圧力に差があれば体積の変化があるので安定ではないことは感覚的に良く分かる.気になるのは 3 番目の式だ.これは何やら複雑そうだが,もっと簡単にできる.平衡時には T_a =T_b であるので,両辺にそれぞれ T_a , T_b を掛けてやっても等式は変わらない.それで, と書き換えられる.これは見覚えのある形だ.ギブスの自由エネルギーの定義式である.つまり,もう一つの平衡条件は,液相と気相それぞれの「1 モルあたりのギブスの自由エネルギー」が等しい事であるようだ. これは一体何を意味するのだろうか.後でじっくりと考えることにしよう.

定温、定積条件での平衡

今度は別の条件で試してやろう.断熱容器を使うのをやめて,外界との熱のやり取りが自由に行えるようにする.そして容器全体を大きな水槽に沈めて,簡単に温度が変化しないようにしてやろう.つまり,定温,定積の条件を実現するわけだ.

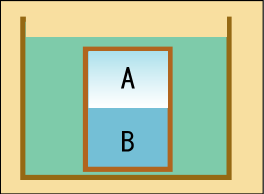
このような場合,が極小になるところで状態が安定するのだった.それで,容器全体のヘルムホルツの自由エネルギーを次のように表現するところから始める. 先ほどと同じ理屈で「1 モルあたりの自由エネルギー」として F_a , F_b を導入した.そしてこれを元に 1 次の変分を計算してやる. 式がさっきより簡単な形にまとまっているが,今回は温度一定なので δT_a や δT_b は 0 としてよいと判断したからである.しかし残念ながら体積についてはそうするわけにはいかない.全体の体積は一定でも, V_a , V_b は変化するからである.

束縛条件も前とは少し違いがある.今回は外界と熱のやり取りがあるので「エネルギー一定」という条件は使えない.使えるのは「全体の分子数は変化しない」ことと「全体の体積は変化しない」ということだけである. これの変分を計算して, を得る.これらを使って再びラグランジュの未定乗数法に当てはめよう. を計算すると, であり,各項が 0 になるべきことから, が得られる.つまり, であることがこの度の平衡条件である.先ほどと比べて「2 つの相の温度が等しい」という条件がなくなったが,これらの温度は共に外界と同じになっているから式で表すまでもなくこの条件は守られている.2 番目の式はやはりギブスの自由エネルギーの定義式の形をしていて, であることを意味している.つまりは,前と全く同じ結果が導かれてしまったということだ.

定温、定圧条件での平衡

さらに別の条件も試してみよう.今度は体積も変化できるように容器にピストンをつけてやる.ただし内部の圧力が常に一定に保たれるように,ピストンの上におもりを載せておく.こうすれば定温,定圧条件を実現できる.

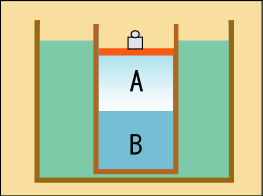
恒温槽に浸された一定圧力が加えられた容積可変の箱の中で二つの相が共存している状況を描いた図

このような条件では,が極小になる状態が安定なのだった.今までの議論と同様に,全体の「ギブスの自由エネルギー」をのように表そう.そして今までと同じように 1 次の変分を計算してやるわけだが,は (T,p) の関数であって,今回はもも一定なので計算は非常に簡単だ.また束縛条件は,全体の体積も全体のエネルギーも変化してしまうので, だけしかない.よって,一気に計算するが, となる.今回もやはり「1 モルあたりのギブスの自由エネルギー」が等しくなるところで釣り合うというのである.温度や圧力は外から与えられており,当然どこでも等しくなっているだろう.つまり,先の 2 つの例と同じ結果が導かれたわけだ.

化学ポテンシャル

こうして,これまで脇役のような扱いだったギブスのエネルギーが,突然,主役の座に踊り出てきてしまった.等温等圧条件でしか意味を持たないと思っていた概念が,モル数変化を伴う平衡条件を考える時にはいつでも共通して使えそうなのである.

しかしこれは偶然と言うわけではない.例えば 3 番目の例である「等温等圧」条件で平衡状態に達したところでピストンをそっと固定してやれば「等温定積」の状態に移行するわけだが,そんな違いだけでいきなり平衡が崩れてしまうわけではないだろう.また,そのまま周りを断熱壁で包んでやったからと言って,内部の様子が突然変わってしまうことはないはずだ.同じ条件で釣り合ってなければ逆におかしいのだ.

まぁ,理屈では確かにそうだが,特にそのために小細工をしたわけでもないのに,ちゃんと辻褄の合う結果になるのが不思議である.なぜかどの場合でも「ギブスの自由エネルギー」でなければならない理由があるのだ.しかし大切なのはその総量ではなくて,それぞれの 1 モルあたりが持つエネルギーであるらしい.「1 モルあたりのギブスの自由エネルギー」と何度も繰り返すことになるのは非常に面倒なので,今後はこれを「化学ポテンシャル」と呼ぶことにする.これが物質の化学的変化に非常に関わりのある量だということが後で分かってくるだろう.

化学ポテンシャルの具体的な意味や,なぜ化学ポテンシャルが等しい事が平衡条件として必要なのかについては,一旦休憩して次回で説明することにしよう.奥が深いので少し話し始めると止められなくなる恐れがあるからである.

冒頭で話した低気圧下で沸点が下がる話まで行けなくて心残りだが,ちゃんと覚えているので安心して欲しい.次回は何としてもそこまで説明したいと思う.