素粒子論：図形的解釈の試み

前回の話を視覚化する

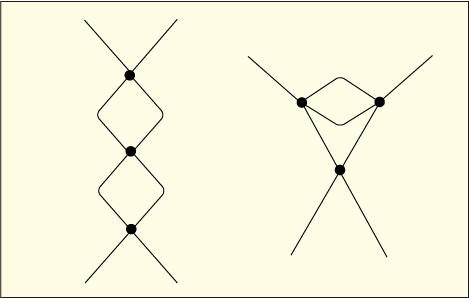
前回の4乗理論の 2 次の摂動計算はあまりに複雑だった.もっと楽に計算結果だけを得る方法はないものだろうか？とりあえず規則性を直観的に把握してみたい.前回の状況を図にすると次のようになるだろう.

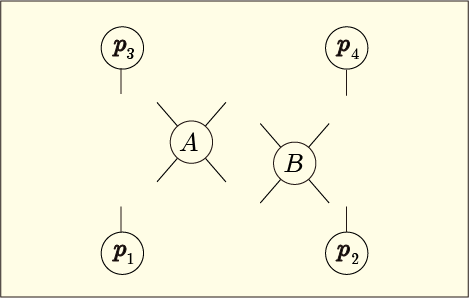
下方に置いた $p_{1}$ と $p_{2}$ が初期状態を表しており,上方に描いた $p_{3}$ と $p_{4}$ が終状態を表している.これらは実際は「運動量 p_i の粒子が存在すること」を意味する演算子なのだった.

そして中央にはそれらと戦う 2 つの部隊が配置されており,前回の記事中では A 班,B 班と呼んでいたのだった.それらからそれぞれ 4 つずつ出ている線は 4 方面に部隊を繰り出せることを意味している.実際には 4 つの演算子である.

最終的にこれらの演算子は一つも残ってはいけないので……というのはつまり,演算子が残ってしまうような項は 0 になってしまうので,演算子どうしを反応させることでデルタ関数だけを残すようにしなければならない.これらを線で繋ぐことで,どの演算子とどの演算子とを対応させるかを表すことにしよう.

ただし,同じ班から出ている線どうしをつなぐことは禁止されているのだった.その上で,「全ての線は区別できるものと考えて」あらゆるつなぎ方の組み合わせを考えるのである.そうやって作った組み合わせの一つ一つが,一つの項を表していることになる.

毎回このような凝った図を描く必要はなくて,実用的にはもっと略した書き方で十分である.A 班や B 班を表す部分は小さな点を書くだけで構わないだろう.そのように描いてみた一つの例として次のような接続図が考えられる.

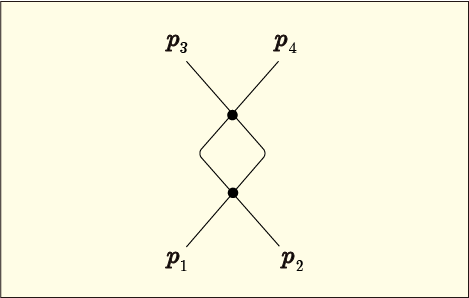
この黒丸で表した部分のことを「頂点」あるいは「バーテックス (vertex)」と呼ぶ.また,頂点どうしを結んだ線のことを「内線 (internal line)」と呼ぶ.これは前回の記事で「同士討ち」と表現していたものを表しているわけであるが,だからと言って「内戦」と書いてしまわないように気を付けよう.初期状態や終状態へと繋げる線は「外線 (external line)」と呼ぶ.

先ほど,「接続の組み合わせ方の一つ一つが一つの項を表している」と書いたが,もう少し正確に説明しておく必要がありそうだ.前回の解説では,階段関数を付けることによって分けた項を別々の項として数えていたのだった.しかし今回の図による解釈では,一つの内線は演算子の順を変えた二通りを同時に意味していることになっている.それらの二通りに数えていた項は計算途中では複雑に絡み合っていたのだが,前回の最後にやったような計算によって「ファインマンの伝播関数」としてまとまった形で一つ一つを分離してやることが出来るのである.これが内線と対応している.つまり,ある接続図の中に内線が 1 本あれば,それはその接続図が表している項の中に一つの伝播関数があるということである.

外線については,それに対応した演算子は生成演算子か消滅演算子かのどちらか一方しかないので,演算子の順序の入れ替えを気にする必要はないのである.では,一本の外線に対応して項の中に現れるのは何であろうか？それは指数関数なのであるが,それについてはこれから,前回の計算結果と見比べて考えてみることにしよう.

同じ形に見える接続はどれも同じ式になるので,式をまとめることができる.一体どれだけの組み合わせが同じ形の接続を作るのかを数えることにより係数を決めることができるというわけだ.

前回の結果との比較

前回の計算結果を見ながら,どんな図と対応しているのかを考えてみよう.最終的に得られたのは次のような式であった. 前回の状況では内線は必ず 2 つ必要なのでどの項にも 2 つの伝播関数が入っており,共通部分としてまとめて 1 行目に放り出されている.2 行目のカッコの中には一つにまとめられなかった 3 通りの項があり,これらに対応して 3 通りの図が描けるはずである.

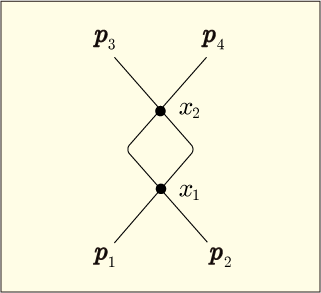
第 1 項を分解すると次のような指数関数が集まって出来ている. これは $p_{1}$ を頂点 $x_{1}$ に, $p_{2}$ を頂点 $x_{1}$ に, $p_{3}$ を頂点 $x_{2}$ に, $p_{4}$ を頂点 $x_{2}$ にそれぞれつないだ結果を表しているようなので次のような接続図に対応しているのだろう.

同様に考えると第 2 項は,頂点 $x_{1}$ につながっているのは $p_{1}$ と $p_{3}$ であり,残りは頂点 $x_{2}$ につながっている.これを図にすると次のようになるだろう.

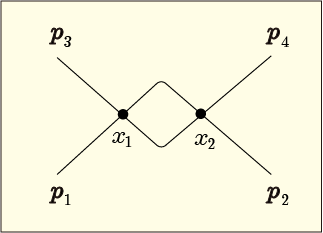
さあ,この 2 つ以外にどんな図形が描ける可能性が残っているというのだろうか？第 3 項を見ると,頂点 $x_{1}$ につながっているのが $p_{1}$ と $p_{4}$ で,残りは残りは頂点 $x_{2}$ につながっているようである.図にしてみよう.

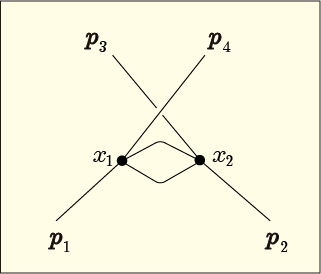
なんと,この接続は第 2 項の図で上に伸びていた 2 つの線を交差させただけのものである.これは第 2 項と同じ図形だとはみなされなかったということなのか！？ということは,この他にも次のような図形も考えられるように思えるがどうして前回の結果の式には対応するものがないのだろう？

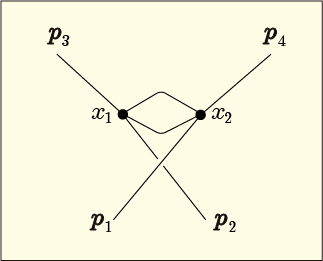
この図は第 3 項の図形をくるっとねじって上の交差を解いてやることで同じにできるということらしい.それぞれの頂点は対等なので,頂点の位置を入れ替えて出来る図形は同一のものとみなしてもいいようである.そう言えば,前回の記事ではそのような式変形の操作をしてまとめたのだった.

そう思ってさらに見直すと,第 1 項を表した図でも,二つの頂点を入れ替えたものが同一だと見なされて一つの項にまとめられているようである.

図さえ描けば計算すべき項が全て導き出されるとは言っても,このような感じになっているので,全ての図を間違いなく,漏れなくダブりなく描き出すというのはなかなか難しかったりするのである.計算や思考の補助としては大変に役に立つだろう.

最も大切なのは,あらゆる接続の組み合わせが計算結果に反映されるという,最初に話したルールだけである.それさえ分かっていればあとは自力で考えられるような話でしかない.

1 次の摂動の図

1 次の摂動についても同じような視覚化ができるだろうか？1 次の摂動は内線が一つもないような状況であり,次のような状況を想定して接続を考えることになる.

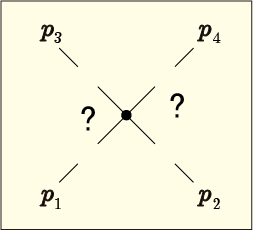
この時点ではまだどの線をどこに繋ぐかは決まっていない.頂点から出ている 4 つの線を全て「区別できる別々のもの」と考えてあらゆる接続をしていくという規則はこの時も成り立っている.組み合わせは通りあるのであり,どう繋いでも次のような同じ形の図にしかならない.

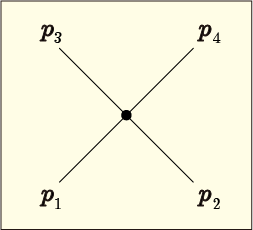
それで計算結果がひとつにまとめられて倍されるわけだが,それをちょうど打ち消すように相互作用項の係数が λ/4! と決められていたのだった.

図との対応ルールのまとめ

ここまでに説明したルールが 3 次以上の摂動でも成り立っているかどうかはまだ検証していないわけだが,先取りして話してしまうことにしよう.スカラー場に限ってはちゃんと成り立っているのである.

今までの話から規則性は想像できると思うが,一応まとめて書いておこう.次の摂動では頂点の数が個になる.それに合わせて各項には次の要素が入る. さらに,使った内線の本数と同じだけの伝播関数が入ってくるが,3 次以上の摂動では頂点が 3 つ以上あるので,どの頂点どうしを結ぶ内線であるかによって伝播関数の変数部分の表記が変わってくる.例えば頂点 x_q と頂点 x_r を結ぶ場合には次のようなものが入ってくるということである. 伝播関数の定義に虚数単位が含まれているのでで割っているのである.

頂点 x_s と初期状態 p_t を結ぶ外線があれば, が入り,頂点 x_s と終状態 p_t を結ぶ外線があれば, というものが入る.外線が初期状態と結びつくか終状態と結びつくかによって指数関数部分の符号が違っているわけだ.

3 次の摂動の具体例

3 次になると頂点が 3 つになる.すると頂点から出てくる線の数は合計 12 本になる.外線を 4 本だけにするためには,8 本を何とかしなければならないのであり,そのために,どんな接続を考えようとも内線が必ず 4 本必要になる.

例えば次のような接続が考えられるだろう.

さらにはこれらを横倒ししたものや,外線の一部を交差させたものも別の図形として扱われることになる.具体的なイメージを一目見せておきたかっただけであり,ここでこれ以上論じるのはやめておくことにする.

問題設定の拡張

ここまで,初期状態と終状態をどちらも 2 個の粒子があるような設定で考えてきたが,図と計算内容にこのような対応があるのなら,初期状態と終状態の粒子の個数を変えたりしても計算できそうだ.例えば初期状態を 1 個にして終状態を 3 個にしても良いだろう.

ただし,頂点からは 4 本の線が出ていて,内線をつなぐたびにそれが 2 本ずつ失われるのだから,頂点を幾つに増やしても外線の数は必ず偶数にならなければならない.

すると,初期状態と終状態の粒子の合計が奇数のような場合については図を使って計算できないことになる.これは理論の不備ではなく,このような設定ではどの項も生き残れないことを意味しているのだろう.そのような現象がそもそも起きないという理論的予測が成り立ちそうだ.

摂動論というのはこのようにして,現実に起こり得る反応がどんなものであるかを説明してくれる理論でもあるというわけだ.自然がこのような理屈に従っているというのも不思議な話である.

電磁相互作用の図形化

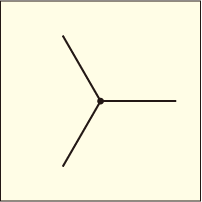
これくらいのことが分かるようになってくると,まだ試していない計算についても類推が出来るようになってくる.電子と電磁場の相互作用項は次の形に書けるのだと紹介したことがある. 2 つの電子場 $\bar{ψ}$ ,と 1 つの電磁場 A^μ から出来ている.ということは,この場合には一つの頂点から伸びる線は 3 本なのであろう.

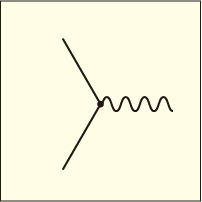
しかし電子場と電磁場の演算子はそれぞれ無関係な場に関するものなので難なく順序の交換が出来てしまうのだった.つまり電磁場どうし,あるいは電子場どうしの演算子でなければデルタ関数を残すことができない.こういう事情により,内線や外線の接続の仕方に制限が生まれるわけである.そこで,どの線とどの線を繋いでいいものかを分かりやすくするために,電磁場を波線で,電子場を実線で表すことにしてみよう.

しかしこれだけではまだ足りないのである.というのも,電子場はスピノルを含んだ形で表されており,互いにディラック共役になっている相手と積を作ったときにしか結果が残らないのであった.それを表すために,2 つある実線にそれぞれ別方向の矢印を付けることにしよう.矢印の方向が一致するような相手としか接続が出来ないというルールを課すわけである.

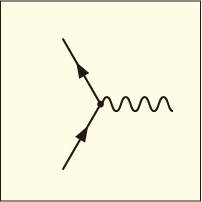
これが電磁相互作用を表すための最小単位だというわけだ.例えばこれを使った 2 次の摂動を考えると次のような接続が考えられるだろう.

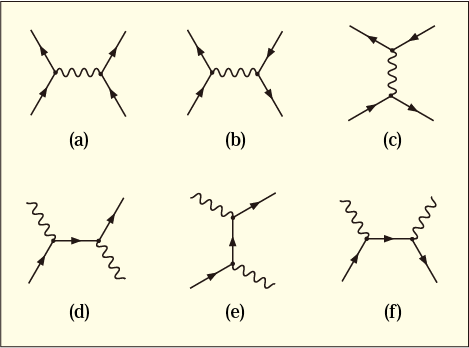
この矢印は接続の仕方を決めているだけのものであって粒子の進む方向を表しているわけではないのだが,電子が矢印に従って進み,反粒子である陽電子は矢印に逆らって進むというイメージを持って眺めてやると,状況を正しく解釈できるようになっている.

例えば (a) は電子どうしの間に電磁気力が働いて異なる運動量になって出ていく「電子・電子散乱」を表している.(b) や (c) は電子と陽電子の間に電磁気力が働く「電子・陽電子散乱」を意味しているのだろう.(d) や (e) は電子と光子が衝突して互いに方向を変える「電子・光子散乱」で,図の矢印の方向を逆にすれば陽電子と光子の散乱を意味するようになる.(f) は電子と陽電子が対消滅して 2 個の光子を生じる過程を表しており,上下を逆にした図にすれば,2 個の光子から電子と陽電子が対生成する過程を表すことになる.

このようにして,幾つかの異なる名前で呼ばれている現象が,どれも一つのルールだけから導き出されることになる.これは驚くべきことだ.対生成や対消滅といったドラマチックに思える現象も,自然にとってはそれ以外の現象とあまり変わりがなく同じ原理で起きるというのだ.

互いに接続可能な線の制限があるため,図の組み合わせの数はスカラー場の理論のときよりもずっと少なくなる.スピノルなどの議論を無事にクリアできれば,スカラー場の計算よりもずっと簡単になりそうな気がする.

果たして本当に簡単に済むのか,どんな困難が待ち受けているかはあとの楽しみにしよう.