素粒子論：ウィックの定理

見た目ほど難しくないのでご安心を

ここまでにやってきた摂動計算の手間を少しでも減らしたい.毎回,最初に初期状態と終状態を設定をしてから場の演算子を展開して,それを眺めて解き方を考えるというのはいかにも効率が悪そうである.結局は生成演算子や消滅演算子の順序を次々と変えていく作業をするだけなので,何か規則性がありそうな気もする.

その規則性というのは前回の図形的な解釈によってかなりはっきりしてきたわけだが,それが成り立つことについては 2 次の摂動までしか確かめておらず,3 次以降でも成り立つことの説明がまだなのだった.

スカラー場だろうがベクトル場だろうがスピノル場だろうが,それぞれの場の演算子には生成演算子と消滅演算子が一つずつ含まれているだけである.わざわざ展開する作業を経ないで,場の演算子のまま,ある程度まで式を簡略化できるとありがたい.そんないい話が,あるのだ.それが「ウィックの定理」(Wickの定理）である.

まずはウィックの定理がどんなものかを書いてしまおう.これまで場の演算子をスカラー場だとかベクトル場 A^μ だとかスピノル場だとか書いてきたが,この定理はそのような違いに関係なく成り立つので, A,B,C,D,… のように表すことにする.

2 次以上の摂動を考えるときには時間順序積が出てくるので,それぞれの場の演算子の時刻を気にしなくてはならないだろう.つまり, $A(x_{1}),B(x_{2}),C(x_{3}),…$ のように表す必要があった.この x_i というのは (t_i, x_i, y_i, z_i) を略記したものであって,この中の t_i の大小関係が時間順序積で問題になるのである.しかしウィックの定理ではそのような時刻の変数をはっきり書いておく必要がない.とりあえず全ての場の演算子の時刻はどれも異なるという前提でウィックの定理を表現してみよう.

本当にそんなものが使い物になるのだろうか？摂動計算では幾つかの場の演算子が同じ時刻を持つグループ（前々回の解説では「班」と表現していた）を形成しているのだった.全ての場の演算子の時刻が異なることを前提にした定理ではそのような状況に対応できないのではないだろうか？まぁ,安心して欲しい.時刻が同じ演算子を含む場合にはさらに結果を簡単化して使えるのである.それについては後で話そう.

まずは見て欲しい.ウィックの定理は次のようなものである. なるべく簡単に見えるようにするために色んな情報を省いているので,残念ながらこの式だけを見て意味を完全に理解することは出来ない.この右辺のように展開する意図すらも理解しにくいだろうと思う.しばらく我慢して説明を聞いてもらいたい.

ABCD…Z というのは有限個の場の演算子の積を表している.個数は幾つでもよくて本当は 1 個でもいいのだが,有限個であってどこかに終わりがあるということで,最後はとりあえずで表しておいた.

ではまず右辺の第 1 行目から見ていこう. N(ABCD…Z) と書いてあるのは正規積を意味している.演算子を展開した後に現れる生成演算子や消滅演算子を全て,生成演算子を左に,消滅演算子を右に並べ替えよという意味である.え！？ちょっと待って！そういう面倒くさい展開などをしなくて済むための定理じゃなかったのかよ？！そうだな.まずはそういった感じの「Wick の定理の意図への誤解」を解くところから始めないといけないようである.

普通の教科書では学問的な事実だけを説明しようとするので,Wickの定理の意図などというものはわざわざ書かないものである.

展開して並べ替えるくらいのことは大して難しくはない.あとでやったらいいだろう.ひとつ気を付けるべきことは,フェルミオンの同種粒子の生成消滅演算子の順序を変えるときだけは,順序の入れ替えをするたびにその項の全体に -1 を掛けなくてはいけないということである.このルールはこれ以降に出てくる正規積 N(…) のところでも適用する必要がある.

(1) 式の右辺の第 1 項が意味しているのは,1 次の摂動を計算したときの情況である.ファインマン図でいうところの「内線」が無い情況,このサイトの説明で言うところの「同士討ち」が発生していないような情況である.展開して並べ替えた結果として同じ形になる項ばかりなので,結局はそれらを数え上げないといけないことになる.ウィックの定理が楽にしてくれるのはその部分ではないのだ.

次は (1) 式の右辺の 2 行目を見てみよう.ここでは <0|}T[AB]|0>} というものが出てくるが,これは一例に過ぎない. ABCD… の中から二つを選んでペアを作り,のように書いて,選ばれなかったものを元々の順番通りに N(…) の中に入れる.可能な限りの組み合わせでそのような項を作るのである.ペアとしては例えば, AB,AC,AD,…,BC,BD,BE,…,CD,CE,CF,… のようになる.何が言いたいかというと, <0|}T[AB]|0>} と <0|}T[BA]|0>} は同じとみなすので,区別してはいけないし,2 倍する必要もない.

これはファインマン図でいうところの「内線」が 1 つだけある情況を表している.

右辺の 3 行目では二組のペアを選んでいる.選ばれなかったものは全て元の順番通りに N(…) の中に入れる.あらゆる可能なペアの選び方を考え,その数だけ項が続くことになる.これは内線が 2 本あるような情況を意味している.

右辺の 4 行目も同様である.ここではあらゆる可能な方法で三組のペアを選び,その組み合わせの数だけ項が続くことになる.

前回までの解説では,まず最初に初期状態と終状態を決めてやって,その状況についての 1 次の摂動,2 次の摂動,3 次の摂動と別々に考えてきたわけだが,ウィックの定理ではそんなことはお構いなしに,場の演算子の並びだけからあらゆる可能な項へと展開するという形の公式になっている.

普通は,これから何次の摂動を計算するぞ,と決めてやって,それによって場の演算子の並びが決まることになる.そこにウィックの定理を使うことになるので,使わないで終わる項も多数出てくるのである.使わない項というのはどれのことだろうか？ウィックの定理ではペアとして選ばれなかった演算子が正規積 N(…) の部分に入っており,これらがファインマン図で言うところの外線として使われることになる.つまり,正規積の中に入っている演算子の数とこれから計算しようとしている情況の外線の数が合ってなければそれらの項は最終的に消え失せる運命であり,計算を始める前にバッサリ切り落として無視してやればいいのである.

伝播関数の定義

なぜ正規積 N(…) の中に入っている演算子だけが外線として使われると言えるのだろうか？そこをはっきりさせるために <0|}T[AB]|0>} などのように書かれた部分に注目してみよう.これは <0|} と |0>} に挟まれていることからも分かるように,もはや演算子ではなく,何らかの複素数値である.これだけの説明では分からないかな？生成消滅演算子が <0|} と |0>} に挟まれていると 0 になるか,さもなければデルタ関数だけを残して消えてしまうのだったことを思い出してみよう.ここで挟まれているのは場の演算子であるから,そのデルタ関数を含む何らかの関数が積分されたものだけが残るというわけである.

実はこの部分に虚数単位を掛けたものが「伝播関数」と呼ばれるものになっている.厄介なことに,伝播関数を意味する記号は <0|}T[AB]|0>} のの部分がスカラー場であるかベクトル場であるかスピノル場によって異なるので,3 通りの書き方で見せておかないといけない. この右辺の虚数単位は付けないで定義されることもある.伝播関数の計算方法は次回の記事で説明することにしよう.

前々回に話した伝播関数の定義とは違った形をしているが,実は同じものであることが後で分かる.それも次回の記事で説明することにしよう.

この (2) 式の定義を見て,何か違う気がするな？と思う人がいるかも知れない.実はこのような定義の他に,これをフーリエ変換したような形の,変数のところがエネルギーや運動量として表された伝播関数もあって,それも同じ記号で表されるのでちょっと紛らわしい.変数の記号を見て区別するのである.その辺りも次回に説明することにする.

とにかく,このような具合であり,残された正規積になっている部分だけが演算子なのである.これらは初期状態と終状態を表す生成消滅演算子とぶつかり合ってきれいに消えてしまわない限りはあとに何も残せないのである.

異なる種類の場が混じっている場合

ここまではまだスカラー場の例しか詳しく計算していないが,電磁相互作用では電子場と電磁場が混在した状況が出てくる.この場合に伝播関数のようなものを計算しようとしても,それぞれの場の中にある生成・消滅演算子は交換できてしまうのでデルタ関数を残さない.つまり全部消えて 0 になってしまう.

ということは,先ほどあらゆるペアを考えるとは言ったものの,異なる種類の場についてはペアを作ることに意味がないわけである.つまり,同種の場だけをペアにしてやればいい.これは前回の最後に電磁相互作用の内線のつなぎ方を少しだけ図で説明したのと重なる話である.

(2) 式でスピノル場の伝播関数 S_F(x_i-x_j) の定義がと $\bar{ψ}$ の間でしか定義されていないのもそのためである.それ以外の組み合わせでペアを作ることは意味がないからである.

混合T積

場の理論で実際にウィックの定理を使うときには, のような繰り返しになっていることが多い.摂動計算では必ずこの形で出てくる.この書き方だと分かりにくいので,もう少し簡略化して次のように書いた方が分かりやすいだろう. つまり,同時刻の場の演算子が幾つも混じることになる.この場合,どう扱ったらいいかというと,あらゆる組み合わせのペアを作るときに,同時刻の演算子どうしのペアは除外するのである.それだけでいい.

これは数学的にそれが成り立つというよりは,便宜上の作法であろうと思われる.

場の演算子がただの生成・消滅演算子の線形和であったなら同時刻であろうが (1) 式が成り立っているのだが,実際には指数関数が掛けられた上で積分が使われており,同時刻の演算子どうしでこれを実行すると問答無用で無限大に発散してしまうのであった.（このため,以前の説明では同じ班での同士討ちを禁じていた.）

というわけで,素直にそのような項を最初から除外してしまおうという考えでこういうことをするわけである.

ウィックの縮約記法

(1) 式が主張している内容は分かってしまえばとても単純なのだが,式で表そうとすると分かりにくい.そこで,次のような記法が使われる.

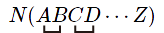
ペアとして選ばれた演算子どうしを線で結ぶのである.これなら,どこにあった演算子が取り出されることになったのかが把握しやすい.あらゆるペアを選ぶのだから,この線は次のように交差することもある.

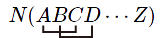
このような表現を「ウィックの縮約」と呼ぶ.選ばれたペアは正規積の中から取り出されて <0|}T[AB]|0>} のような箱の中に入れられるのだが,わざわざそのように書き直すと場所を食うだけだし分かりにくくなるので,この書き方をそのまま数式として採用してしまおうというわけである.つまり,次のような等式が成り立つかのように,わざわざ右辺のような形に直さないで使うわけである.

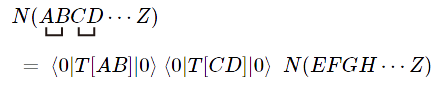
残念ながらウェブページ上でこの書き方をする簡単な方法は今のところ用意されていないので,この解説では使わないことにする.

LaTeX にはそのような記法をサポートするパッケージがあるので,PDF文書として公開する形でなら書けるのだが,このような HTML 形式で書かれたサイトの場合にこのような表示をするためには数式を画像ファイルとして別に作る必要があって面倒なのだ.実際,上の 3 つの式だけは透過処理を施した画像ファイルである.

証明はしないけど大雑把に説明しておく

結局のところ,「あらゆるペアを選んで,それと同じだけの項に分かれて,その選ばれたペアが伝播関数と同じものになる」というのは,「あらゆる内線を考えるという図形的操作」と同じであるし,それ以外の正規積の部分は「あらゆる外線を考えるという図形的操作」と同じになるわけで,前回の話に理論的根拠を与えているのがこの定理だというわけである.

あとは,この定理が正しいという実感を持ってもらうことだけが重要である.そんなことは気にせず使えるという人は別にそれでもいいだろう.

そもそも <0|} や |0>} は (1) 式の左辺には使われていなかったのに,どこから,どんな理由で出てくるのだろうか？また,ボソンとフェルミオンの場合で交換関係が違っているはずだが,それでも同じ形の定理が成り立っているのはなぜだろうか？

前者の疑問については,実はそれほど面倒な話ではない.二つの場をペアにしたときにそれを展開してやると $\hat{a}\hat{a}, \hat{a}\hat{a}^† , \hat{a}^†\hat{a} , \hat{a}^†\hat{a}^†$ という 4 通りの演算子の並びができるのだが,この中で $\hat{a}\hat{a}^†$ という並びになっている項をひっくり返したときに出てくるデルタ関数だけを右辺に反映させたいので,他の要素を消すための道具として <0|} と |0>} を使っているだけなのである.

また,後者の疑問についても大したことはない.正規積を作るときには,フェルミオンの演算子どうしを交換するときだけ,そのたびに -1 を掛けるという操作が要るということを先ほども話した.それはこの定理を適用した後でユーザー側の責任として行うことなので,定理の側としてはサポートしなくて済んでいるのである.

これ以上の細かい説明を始めると話が長くなってしまってどこでやめたらいいのか分からなくなるので,具体的な証明は興味のある読者にお任せして,これくらいで終わらせることにしよう.