なぜ発散してしまうのか２

まずは状況の観察から

前回の続きである.前回の最後に出てきた次のような積分が発散することを説明したい. ここに使われているというのは4元運動量であり,次のように解釈する必要がある. このように記号を変えて書くならば, d^4 k という表記の方も次のような意味のものを略記したものであることを思い出す必要がある. 一方, (k+p)^2 の方はもう少し面倒くさい形になる.ここで使っている 2 乗というのも 4 次元的内積を意味しているものだからである.というのは 4 成分の定数ベクトルであるから,その成分が (E,p_x, p_y, p_z) だと決めてやれば次のように表せるだろう. ああ,脅かして申し訳なかった.4 次元的内積と言っても,普通の内積の計算のように展開して問題ないのだな.しかし,(3) 式のような 4 つの変数で順に積分していくのだから,(4) 式の最後の形のようなすっきりしたものを使うわけにも行かず,その前の途中式のようなものを (1) 式に代入して考えないといけないのだろう.

このような複雑そうなものを真面目に計算するのは出来るなら避けたい.結局は発散してしまうのだと聞かされていればなおさらだ.発散してしまうかどうかだけを手早く見極めることができるような便利な方法は何かあっただろうか？

例えば 1/x という関数は無限大まで積分すると発散するし,積分範囲を 0 に近付けても発散する.ところが 1/x^2 ならば無限大まで積分しても発散しない.ただし積分範囲を 0 に近付けると発散してしまう.(1) 式の分母を見るとただの k^2 よりも速く大きくなるようだし,発散しないのではないかという気もしてくる.

さらにじっくり眺めていると, (ω,k_x, k_y, k_z) の各成分の組み合わせによって,(1) 式の分母が 0 になってしまう瞬間が必ずどこかにあるのではないかということも心配になってくる.発散はそれが原因で起きるのだろうか？どの変数から先に積分してみてもそのような特異点を踏んでしまう可能性があるし,状況が把握しづらい.

Wick回転

まずは特異点の問題から何とかしてみよう.変数の積分はもちろん実軸上を (-∞,∞) の範囲で実行するのだが,一旦そのことを忘れて,を次のような複素平面上の経路で積分することを考えてみよう.

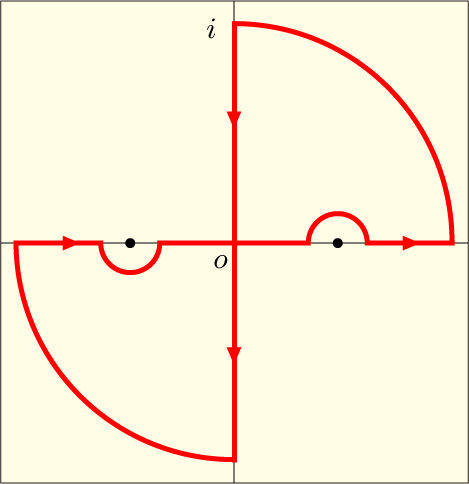
この図ではコースを小さく書いてあるが,実軸上の無限遠にまで行ってから,無限遠の円形コースを通って虚軸の無限遠に向かい,虚軸を真下に降りてきて,再び無限遠の円形コースで実軸の負の無限大に至るという壮大な一周コースであることを表し切れなかったのである.実軸上には特異点があるが,この一周コースの内側には特異点が無いようにしてある.内側に特異点がない一周積分の結果は 0 になる.無限遠を通る円形コースの部分も今回のような形の関数では 0 であろう.すると,実軸上に沿った (-∞,∞) の積分の値と,虚軸上に沿った (-i∞,i∞) の積分の値は,等しいと言えるだろう.

実軸上のコースがわずかに特異点を避ける形になっているのがずるをしているようで気になるかもしれない.しかしファインマンの伝搬関数は厳密には ε を使って特異点を上下にずらす形で結果が得られたのだったから,今回の (1) 式の分母にもその ε が入っていると考えて,そのせいで特異点の方がわずかに上下にずれていて,実軸上のまっすぐな積分をしても同じ結果が得られるのだと考えてもいいのである.そういう厳密さにこだわりのある教科書ではファインマンの伝搬関数の分母に +iε を残したままにしてあるのだが,私は細かいことを気にしない性格だし,ε を導入しない別解法で求めたこともあって,早々に考慮から外してしまったのだった.

これはとてもありがたいアイデアだ.特異点がある実軸で積分するのではなく,代わりに特異点のない虚軸で積分してやれば同じ結果が得られるというのである.つまり,関数の中に含まれるを ω=iω' という式で置き替えをして,を (-∞,∞) の範囲で積分するように書き換えても同じ結果が得られることになる.このようにして特異点を避ける計算テクニックのことを「ウィック回転」と呼ぶ.新変数はを複素平面上で 90°の回転をさせたものだからである.

このテクニックはひょっとして伝搬関数を導いたときの証明の計算でも使えたんじゃないか？と思うかもしれないが,過ぎたことだから今は振り返らないで前に進もう.

これが今回の計算のどこで役に立つかというと,例えば (1) 式の分母にある k^2 -m^2 という部分である.次のように書き換えが出来る. m>0 であるので,他の変数が実数の全域で変化しようとも全体が 0 になってしまうようなことが決して起きない！分母が 0 にならないのだ.つまり,特異点を考慮する必要が全くなくなってしまうのだ.

しかしもう一方の (k+p)^2 -m^2 については ω=iω' の書き換えをしてもこんなに単純な形にはなってくれず,虚数が混じる形になってかえって計算が面倒になってしまう.とは言うものの,虚数が混じることによって分母がぴったり 0 になってしまうことは防げているようだ.

積分の途中で特異点を踏んでしまうという心配は避けることが出来たが,こんな方針で計算を続けることが出来るのだろうか.

発散の条件

幸いにして,この積分が発散してしまうという結果だけは先人たちの努力によってはっきりしている.我々としては,どう頑張ってもこの積分が発散してしまうということに集中して,それを何とかして証明してやればいいのだろう.

例えば,もっとずっと単純な形の級数として展開してやって,それぞれの項が発散するかどうかを見るという方針ではどうだろう？テイラー展開？ローラン展開？うまくできそうにもない.これらの展開には変数の範囲に制限が付くことが多い.無限の範囲で積分しようとしているのだから,そのような制限があっては使い物にならないだろう.そもそも変数が 4 つもあるものをどういう形に展開してやればいいのだろうか？

そういえば,1 変数の単純な関数が発散するかどうかは考えてみたことがあるけれど,多変数の関数が発散するかどうかの条件というのは自分は考えてみた覚えがない.いきなり難しいことをやろうとするのは無理があるので一つずつ確認していこう.

まずは念の為に 1 変数についてだ.次のような積分を考える. これが発散するかどうかは α=1 に明確な境目があって, α≦1 では発散してしまうが α>1 では収束する.そんなギリギリのところのことを考えなくても 1/x^2 では確実に収束するのだ.それだから (1) 式のようなものが収束しないというのは少し不思議に思えてしまうのである.

では 2 重積分ではどうだろうか.2 変数にする必要があるし,2つの変数は対等だということにしておきたいから次のような設定で確認してみよう. あ～,これはやめよう.この先の計算が複雑すぎる.

多重対数関数というのが出てきて,説明に不向きなのである.

(x,y) の原点に特異点があることを承知で積分範囲を次のように変えてみよう. この最後の積分は 1/x の積分と同じで,積分範囲を 0 に近付けても発散するし,積分範囲から 0 を除外しても発散するのである.

このような結果になるのは原点に特異点があるからではないのか,という疑いがまだ拭えないので,特異点をなくすために正の値のを入れて次のような計算をしてみよう.

これなら結果に文句はないであろう.結局,対数的な解になって発散するのである. 1/x^2 というタイプの関数であっても 2 重積分には耐えられずに発散してしまうということが分かる.

よし,ならば 3 重積分ではどうか！とは言ってもこれまでの形の関数では 2 重積分で発散してしまうことが分かったのだから,対抗して 3 乗でやってみよう. と思ったが,これはとても面倒な計算結果になるのである.はここでは 2 乗にしてあるが,分母が 0 になることを防ぐために入れたものなので正の数でありさえすれば何乗でもいい.しかし今回は他の変数が 3 乗になってしまったことでそれらが正にも負にもなることから,分母が 0 になる可能性が出てきてしまった.それでも諦めるわけには行かないから,ある程度の雰囲気を探っておこう.上の式ではまずで積分するのだから,他の部分は定数とでも置いて計算してやればいい.途中式は面倒だが,結果は次のようになる. 積分範囲を勝手に (0,∞) に変えてしまっているのは複雑になりすぎるのを避けるためである.おおよその雰囲気だけを伝えたいのでサボっている.次はこののところに y^3+b を代入して積分してやればいい.とは言うものの,これもまた面倒な式になってしまうだろう.ただ, $1/a^{2/3}$ に y^3 的なものを代入するのだから, 1/y^2 的な式になるだろう.雑な説明で申し訳ないが,もう一度積分すれば 1/z 的な式になって,さらに積分すれば対数関数的な形になって発散するのである.

4 重積分についてはもう具体的には試してみたくもないのでイメージだけにしておくが,あらかじめ 1/x^4 的な式を用意しておいても,積分するたびに 1/x^3 , 1/x^2 , 1/x といった性質を持つ形へと変わっていって,やはり 4 回目で対数関数的な形になって発散するのである.このように,積分結果が最終的に対数のようになってしまって,積分範囲を無限大に飛ばした時に発散してしまうことを「対数発散」と呼んだりする.

(5) 式で再確認したように,発散する直前の段階で 1/x よりもほんのちょっとでも分母の次数が高ければ……,つまり 1/x^α のが 1 より大きければ発散は防ぐことが出来るのであろう.ということは,4 重積分の場合には 1/x^4 よりほんの少しだけでも分母の次数が大きければ発散は防げるのである.しかし 1/x^4 ではギリギリ発散してしまうことになる.

そこで (1) 式に戻ってみよう.4 重積分である.分母に k^4 よりもほんの少しでも次数を増やす要素があれば発散は防げた可能性がある.しかし分母の最大次数は k^4 である.あと少し,足りなかったのだ.

もう少し追い詰める

イメージ的には (1) 式が発散するのは当然だという感じが見えてきたことだろう.しかし議論が雑すぎて,まだ確信が持てない感じもする.そこで反論できないくらいまで追い詰めてやろう.

(1) 式の一部分は,次のように書き換えることが出来る. つまり,(1) 式の被積分関数の全体は次のように書けるということである. この第 1 項は先ほどの議論からしても,いかにも発散が避けられない形である.しかし第 2 項はそれに対してさらに余分なものが付いており,の次数は分母の方が勝っている.つまり,第 2 項は発散を免れることが出来るのである.

とは言っても第 1 項が発散するのであれば全体が発散するのを防ぐのは無理である.第 1 項が発散することを丁寧に確かめてやろう.第 1 項は Wick 回転を使えば次のようにをに書き直して積分しても同じである. これで特異点のせいで発散するわけではないことがはっきりする.あとはそれぞれの変数で (-∞,∞) の範囲で積分してやればいいのである.一部の変数の記号を置き換えた次のような計算が役に立つだろう. このは k_x^2 +k_y^2 +k_z^2 +m^2 を意味しているが,次は k_x で積分したいので他の部分をと置いて積分してやろう.発散することを確かめたいだけなので π/2 などの係数は外していくことにする. このはを意味しているが,次は k_y で積分したいので他の部分をと置いて積分してやろう.係数の 2 も外しておく. このは k_z^2 +m^2 を意味している.いよいよ最後の積分である. こうして,(1) 式が発散してしまうことについて,疑いなく知ることが出来た.