なぜ発散してしまうのか３

これまでのあらすじ

摂動論の計算の例として一番単純そうなスカラー場を選んだのに,2 次の摂動でいきなり発散の問題に巻き込まれてしまった.確率振幅が無限大になってしまうというのだから,この結果が何か物理的に意味のあることを表しているとも思えない.一体どんな計算をしてそんな結果に至るのかを説明するだけでかなり長い話になってしまった.

幸いにして,ここまでの話に出てきた色々な概念や計算法はスカラー場以外にもほとんど同じように使えるし,必ずしも発散するわけではないらしい.

ではなぜ4乗理論の 2 次の摂動ではこのような発散が起きてしまったのだろうか？これ以外の状況について計算した場合にもたびたび同じことが起きるというのなら,この計算法を安心して使っていくことが出来ないではないか.

ここまでの解説では 2 次以上の摂動計算をやっと一つ終えただけであり,まだ 2 次以上で発散しない例には出会っていないのだった.発散が起きた原因をはっきりさせなければこの理論を信用することなどできるはずがないというものだ.

状況の再確認

今回の無限大になってしまった計算は最終的に 3 つの項にまでまとめられ,それぞれを表す図は次のようなものだった.

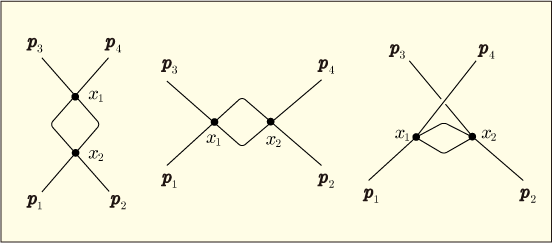
実際に発散するところまでやってみたのは一番左側の図に相当する項だけであるが,どれも同じような計算内容なので結局はどの項も発散するのである.とりあえず一番左側の図で説明することにしよう.

$x_{1}$ , $x_{2}$ と書かれた 2 つの頂点があり,それぞれに流入するエネルギーや運動量の合計は 0 になるという条件が数式から読み取れるのだった.それは要するに,エネルギー保存則や運動量保存則である.内線で表された仮想粒子の運動量を $k_{1}$ , $k_{2}$ として計算したので,これを図に書き入れよう.

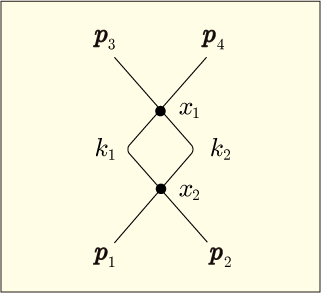
φ4乗理論の2次の摂動で出てくるファインマン図の一つに仮想粒子の運動量を書き込んだ図

これらの $k_{1}$ , $k_{2}$ はどちらも 4 成分の量であり,運動量もエネルギーも表しているのである. $k_{1}$ , $k_{2}$ はそれぞれの成分について全範囲で積分するので,正も負もどちらの値も取り得る.つまり,流入や流出のどちらもあり得る.

さて,頂点 $x_{2}$ で保存則を満たすためには,流入した $p_{1}+p_{2}$ が全て $k_{1}+k_{2}$ として出ていくことが必要である.ところが,例えば $k_{1}$ として大量に流出して, $k_{2}$ として大量に逆流して流入してきても, $k_{1}$ の方が $k_{2}$ より $p_{1}+p_{2}$ だけ多ければ条件は満たせてしまうわけである.

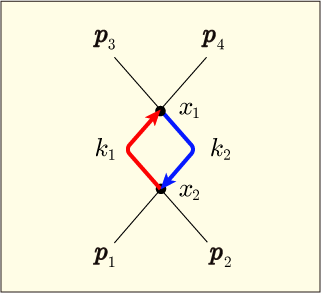
φ4乗理論の2次の摂動で出てくるファインマン図の一つに色付きの矢印を書き込んだ図

$k_{1}$ がほとんど無限大になっても,ほとんど無限大の $k_{2}$ として戻ってこればいいことになる.このように, $k_{1}$ と $k_{2}$ の上限や下限が存在していないのである.

頂点 $x_{1}$ でも同じであって, $k_{1}$ と $k_{2}$ の差額が $p_{3}+p_{4}$ として出ていけば問題ないわけであるから,最終的に $p_{1}+p_{2}=p_{3}+p_{4}$ という条件は満たされることになるが, $k_{1}$ と $k_{2}$ の値を固定するようなものは何一つ無いのである.

第 2 の図や第 3 の図形を使っても同じである. $k_{1}$ と $k_{2}$ の差額が固定されるだけであり,どちらも無限大になることが許されてしまうのである.

ごく小さなエネルギーの粒子どうしの相互作用の裏側で,無限大のエネルギーや無限大の運動量のやり取りが成されている可能性を認めてもいいものだろうか？いや,「いいものだろうか？」とは言っても理論上はこれを禁止するものが見当たらないのである.

防ぐ方法はあるか

場の理論ではない,普通の量子力学の摂動論でもそうだったが,起こり得るあらゆる過程の確率を合計するという形になっているようである.量子力学的には,そのどれか一つが起こるのではなく,どの過程も確率的に重なって起きているかのようにイメージするのが正しいのだろう.

このあたりのことを話し出すと私はすぐ脱線してしまって無駄で不正確な想像を書いてしまいがちになるのでかなり削ったのである.

仮想粒子があらゆるエネルギー,あらゆる運動量を取るという全ての場合の確率を合計してみたところ,発散が起きてしまったのだった.それは積分途中で分母が 0 になるような特異点を踏んでしまうことによって起きたのではなく,積分範囲が無限大にまで広がっていることによって起きたことが明らかになった.

無限大のエネルギーの仮想粒子がやり取りされるということは現実的には起きていなさそうな気がするので,どこかにエネルギーの上限があることにしてやったらどうだろうか？もちろん,それによって積分が発散することは防げる.しかしどこを上限に決めてやったらいいだろうか？それを決める基準が存在していないし,どこを上限に定めるかによって確率が変わってしまう.実験に合うようにそれを決めてもいいが,今度はなぜそこに上限があるのかを説明する必要が出てきてしまうだろう.

それくらいのことはもちろん昔の研究者たちはすぐに試してみたのだろうが,何も面白い結果が得られなかったに違いない.

上限をはっきり決めるのではなく,エネルギーが高い仮想粒子ほど出現しにくくなるような形にしたらどうか,と思うかもしれないが,伝搬関数の形を見ても分かるように,既にそういう形にはなっているのである.それでも発散が起きてしまうのだから,もっといい理屈をひねり出して発散が起きない理論を新たに作り直さなくてはならないことになる.

どういう状況で起きるのか

先ほどの説明から考えるに,同じような発散は簡単に起きてしまいそうである.要するに,計算内容をファインマン図で表したときに,内線がループを形成しているともう駄目なようである.

2 本の同種粒子を表す内線だけでループが形成されている場合に限った話ではない.途中に頂点が幾つあっても,何本の内線でループを作っていようとも,とにかくループがあれば駄目なのである.例えば次のようなものも駄目である.

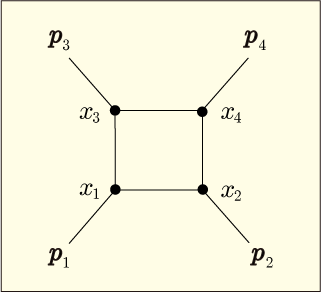
なぜなら,そのループ上を何らかの一定のエネルギーや運動量がぐるぐる回る形に出来るわけだから,それがどんな巨大な値になろうと,流れが逆回りになろうとも,いずれも矛盾なく許されてしまうからである.その全ての可能性を積分しなくてはならなくなり,同じ結果に陥る.

ああ……駄目じゃん……場の理論.

このようなことが起きてしまうのは理論に重大な欠陥があるからではないだろうか？とても使い物にはなりそうにない.これが 1940 年代に「くりこみ理論」が誕生して発散の問題が解決する以前の状況である.当時の場の理論はまだほとんど信用されていなかった.

くりこみ理論については,一通りの説明を終えて落ち着いてから説明を始める予定である.それまでは,発散が起きそうな状況を避けながら話を進めていくことにしよう.

個人的に未解決な問題

以上のような内容で記事を仕上げようと思ったのだが,ループがあれば必ず発散が起こるということを自力で証明できなかったので,長い間公開することをためらっていたのである.

教科書をあれこれ探してもループがあるときに発散してしまうという計算の例は単純なものに限られており,上の図のような 4 つの頂点でループを形成するときにどうなるかを見付けることはできなかった.参考までに,このような場合に発散することを匂わせることが書いてある教科書としては次のものが挙げられる.

・場の量子論〈第1巻〉（日本語訳） F.マンドル / G.ショー (p.189)

これも第 8 章の「輻射補正」という話の中でただ一言だけ書かれているのであって,その章全体がくりこみ理論に関係する話であるから,ひょっとすると全く関係ない文脈で書かれているのかも知れない.今の私はくりこみ理論もほとんど把握できていないので正しく判断することができない.

他の教科書にも似たようなループ図形が出てくることは多いのだが,くりこみ理論で何とかなってしまうからだろうか,あまり発散のことを気にしている様子がなくて不思議である.多くの教科書は発散についての不毛な議論にかかわらないようにしたいのか,さっさとくりこみ理論の説明を始めてしまうのである.

私としては発散は起きないのではないかとすら疑っている.そう疑うならどんな値になるのか自分で求めてみればいいではないかと思うかもしれないが,頂点が 4 つあるということは 4 次の摂動であり,複雑になりすぎる.現在の私の能力では多数の積分を正しく実行することは無理であった.教科書に載っていない理由もおそらく同じようなものであり,実例を載せようとすると長大になりすぎるのだろう.

今,摂動の次数が増えると複雑になりすぎると言ってしまったが,ループがなければあまり恐れる心配はない.積分はデルタ関数によって楽に実行できるし,変数どうしの絡みも出てこないので複雑になることもない.ただし,次数が増えると考慮すべき図形の数が急に増えるので,別の意味で怖い.しかも恐ろしく増えた図形の中にループするものが必ず出てくるだろう.やっぱり怖い.

試してみた計算例

実際に試してみたのが次のような計算である.（悩んだ当時のノートが残っていて助かった）

一つの頂点から 3 つの線が出ているので4乗理論ではなく3乗理論である.最後の積分の中の分子は積分に関係のないデルタ関数であるから無視しても良い.分母の最大次数はの 8 乗であり,積分は ∫ dk と書いてあるが, d^4 k を略して書いてあるだけなので実は 4 重積分である.このように,分母の次数は積分回数に比べて十分に大きいので発散しないような気がするのである.

しかし部分分数分解などをしてやるともっと分母の次数の小さな項が出てきて,それが発散を招く可能性がある.それを検証する気力がなくなって挫折したのであった.前回の記事でも部分分数分解をやって発散する項と発散しない項に分けてやったが,分母の次数が減るどころか,むしろ分母の次数が大きな項が出現して,そっちの方が発散を免れたのだった.今回期待しているのとは逆の結果であって,そういうものを見てしまったことも,試してみる気力を奪われる原因になったのだった.

こうして疑問点をまとめながら久しぶりに考えてみると簡単に解決できそうな気もしてきたが,今は無理せず,とりあえずこのまま公開してしまうことにしよう.