ファインマンの伝播関数

伝播関数の定義

前回出てきた伝播関数の定義は次のようなものだった. このような形で定義されているのは,ウィックの定理から出てくる形式に合わせてあるからである.これらが <0|} と |0>} で挟まれていることの物理的な意味などは考えないほうがいいだろうと思う.2 つの場を組み合わせたときに生じる生成・消滅演算子の並びの中から欲しい組み合わせだけを恣意的に取り出すために使っているだけである.虚数単位をわざわざ付けて定義しているのは今のところ,まだ謎である.なんだか邪魔で仕方がない.

これらの伝播関数のことをわざわざ「ファインマンの伝播関数」という呼び方をすることがあるのは,それ以外の伝播関数もあるからである.今は関係ないので気にしなくてもいい.教科書によってはその辺りを混ぜこぜにして説明してきたりするが,あまり余計な話で初学者を混乱させないようにしてほしいものだ.

まぁ,これは教科書が悪いというわけでもないのである.今は「相対論的な場の理論」の基本を説明しているので伝播関数と言えばこの形なわけだが,物性理論などでは「非相対論的な場の理論」が使われており,理論上の制約が緩いために他の形の伝播関数も使われるし,あちこちの分野でバリエーションが幾つも存在しているのである.著者の専門によってどの形が基本であるかという考え方が違っているというわけだ.

スカラー場の伝播関数

では,これらを具体的に計算してみよう.まず (1) 式のスカラー場の伝播関数からである.

場の演算子の具体的な式はこの解説の流儀では次のようであった. これを (1) 式に代入してやると次のようになる. まずは時間順序積を外すことを考えよう.これは時間の値が大きいものを前に持ってくるというルールであった.時間は $e^{ik_{1}x_{1}}$ などのように書かれている中に隠されている.この $k_{1}x_{1}$ は 4 次元的内積というルールで略した書き方であり,実際は $k_{1}x_{1}=ω(k_{1})t_{1}-k_{1}・x_{1}$ であることを思い出そう.(5) 式の 2 つのカッコのうち,最初のカッコ内の演算子の時刻が $t_{1}$ であり,次のカッコ内の演算子の時刻が $t_{2}$ である.

$t_{1}$ と $t_{2}$ のどちらが大きいかによってカッコの順序を変えなくてはならないが,階段関数 θ(t) というものを利用する. $θ(t_{1}-t_{2})$ としておけば $t_{1}>t_{2}$ の時だけ有効になる項を表すことが出来るし, $θ(t_{2}-t_{1})$ としておけばその逆を表せるので,次のように展開できる. この技は以前に4乗理論の 2 次の摂動を計算したときにも使ったのだった.

次にこのカッコを展開してやることになるのだが, <0|} と |0>} に挟まれて生き残れるのは $\hat{a}\hat{a}^†$ という並びのものだけである.それを考えれば手間を掛けずに (5) 式を次の形にまで一気に変形できる. この演算子も順序を変えてやればデルタ関数だけを残して消えるので, のようになり,さらにどちらかので積分してやるとデルタ関数の働きによって $k_{1}$ と $k_{2}$ の区別も必要なくなり, というあっさりした形にまで変形できる.

以前に4乗理論の泥臭い計算をしたときに,最後の方で出てきたのがこの形である.そのときにはこれを伝播関数の定義として紹介したのだった.この形の方が (1) 式のような形式的な定義よりも伝播関数の意味を直接的に表せていると言えるかもしれない.

階段関数を含む積分

さて,階段関数を含む積分をどのように実行したら良いだろうか.階段関数というのはデルタ関数を積分したものである.いや,階段関数を微分したらデルタ関数になると考えた方がイメージしやすいか.どちらでもいい.デルタ関数というのは積分表示で次のように表せるのだった. 指数関数の肩の部分のマイナスは付けても付けなくても同じになるが,次の式がきれいになるように付けてある.で微分したらこの形になるのが階段関数なのだから,次のような形で表せると考えれば良いのではなかろうか. 分母にがあって,積分の途中で ω=0 となるところがあるので破綻するような気がするが,静かに成り行きを見守っていてほしい.

この (8) 式を (7) 式に代入してやりたいのだが,(7) 式で使っていると (8) 式で使っているは無関係なので,分かりやすい区別をしておいた方が良いだろう.どうせ一時的に使うだけの積分変数であることだし,(8) 式のをで表して代入してやろう. さて,この後の式変形の負担を減らすために, $x=x_{1}-x_{2}$ , $t=t_{1}-t_{2}$ と置いて簡略化しよう. ここからかなり技巧的になるのだが, ω^2 =k^2 +m^2 という関係になっているので k→-k と変えてしまってもの値には影響がない.また, s→-s と変えてしまっても積分範囲はどうせ (-∞,∞) という全範囲に渡っているので大きな影響はない.分母にがあるので全体の符号が変わるくらいである.それをカッコ内の第 2 項にだけ適用するのである. の積分範囲はなので,カッコ内の第 1 項で s'=s+ω と置いてで積分するように変えても大差がないだろう. s=s'-ω と変数変換したと考えてもいい.同様な理屈によって第 2 項は s'=s-ω と置くことにする. なんと！？式の中からを消し去ってしまうことに成功した！そこでだ,というのはもともと角振動数と同じ次元を持つ量だったので,これをチャンスとばかりにに成り代わってしまうことにしよう.なんて恐ろしい子……. こうして記号の乗っ取りに成功した.大抵の教科書は黙々と,しかも途中を飛ばしながら式変形が進むので何をやっているのかが大変に分かりにくいところである.今の説明ではという記号を使って分かりやすくしているが,教科書では $k^{0}$ とが混在していたりして,それは同じものなのではないのか？一体何を区別しているのだ？と悩まされたりする.

さて,この積分を見ると,についての 3 次元の積分とについての積分が使われている.これらを一緒にして,4 次元の積分として d^4 k と表してしまおう. $e^{ik・x}$ と $e^{-iωt}$ も一つにまとめて書けそうだ. 記号を乗っ取っただけでなく,その意味まで乗っ取ろうとしている.一体何が起きているのだ？さらに 4 次元的内積の記法を利用して k^2 =ω^2 -k^2 という置き換えもしてしまおう. まるでが粒子のエネルギーを表しているかのように,粒子の運動量と対等な存在としてまとめられてしまった.しかしは実際はそうではないのだ.が粒子のエネルギーを表しているのならという条件を満たしていなければならない.この条件式は 4 次元的な球殻のイメージなので「質量殻」と呼ばれる.しかし (9) 式ではそのようなエネルギー保存則を破ってはに無関係に (-∞,∞) の範囲で積分されることになる.つまり,質量殻の上に乗っていないというので,このような状況のことを「オフ・シェル」(off shell) と呼ぶ.「オフ・シェルでの積分」のような言い方をする.

「4 次元的な球殻」という説明に違和感を感じる人もいるだろう.どちらかといえば,運動量 k の方がエネルギー ω や質量 m によって決まる 3 次元的な球殻上に縛られているイメージだし,そこにωも含めたいのなら,k と ω とが質量 m によって決まる 4 次元的な双曲面上に縛られていると表現した方が正しいからだ.

(9) 式をよく眺めてみると,何となくフーリエ変換に似ている気がしてくる.よく使われているフーリエ変換とは少し係数と指数関数の符号が違っているのだが,その辺りはフーリエ変換の流儀の違いであって本質的な違いではない.つまり (9) 式は次のような関数をフーリエ変換したものだという見方も成り立つことになる. この式の方がすっきりしているというので,(1) 式ではなく,この (11) 式を伝播関数と呼ぶ場合もある.(1) 式と (11) 式が互いにフーリエ変換の関係にあるというのは後で物理的な意味を考えるときに役に立ちそうだ.

今回計算していたのは (11) 式ではないし,途中で計算を楽にするために変数の置き換えをしていたので,それを元に戻してやると,次のような形が本来の結論である.

複素積分を使った別解法

とりあえず (1) 式についての結論は出たのだが,ついでに少しだけ寄り道して行こう.

多くの教科書では上に書いたような式変形で (12) 式を導くのではなく,もう少しエレガントな方法による証明を好んで使っている.結果である (12) 式の方を何の前置きもなく急に持ってきて,この d^4 k の 4 次元積分のうちのの積分だけを実行した結果として (7) 式が得られることを示すのである.

そのときに複素積分のテクニックを使うので,これはひょっとすると複素空間を行き来する素粒子の神秘的な振る舞いを説明してくれているのではなかろうかと勘違いしそうになるのだが,実はただの式変形の説明なのであって,そこに神秘的な要素は全く無いのである.

いきなり (12) 式が出てくるので,まさか変数の乗っ取りという恐ろしい事件が起きていると気付けるわけもなく,この式が何のために出てきたのかを探ろうとして物理的な意味を読み取ろうとするわけだが,エネルギー保存則を満たさない積分だというのでそこに神秘を感じてしまうのは避けられない.

文句はこれくらいにして,それをやってみせよう.(12) 式というのは,次のような関数をさらにで積分したものだと考えることができる. 見て分かるように, ω = ±√(k^2+m^2) という 2 つの点が特異点となってしまっている.そこで,これらの点を避けるために次のような積分経路を使って積分を行うことにする.

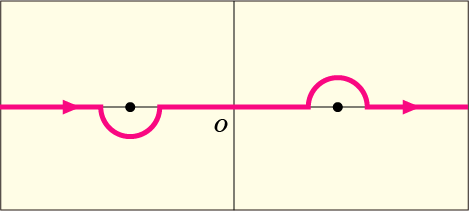
これでは実軸上の積分をしたことにはならないのではないかと思うかもしれないが,それについては後で解決しよう.まずは $t_{1}-t_{2}>0$ だと仮定してやる.このとき,が複素平面の下方に行くほど $e^{-iω(t_{1}-t_{2})}$ の絶対値が 0 に近付くので,実軸上の正の無限大まで積分したあとは,下半面の無限遠の経路を通って実軸上の負の無限大のところへ戻るような一周積分を考えると都合が良い.複素積分では特異点の周りを一周する積分の値は簡単に求めることができるのだった.今の条件では下半面の無限遠での積分が 0 であるので,一周積分の値は全て実軸上の積分値だと言えることになる.この場合, ω=+√(k^2+m^2) の周りの右回り一周積分である.複素積分では左回りを正の方向と考えることになっているので,一周積分の公式で得た結果に -1 を掛けてやる必要がある.

1 位の極である特異点の周りを左回りで一周積分するときの公式は次のようなものだった. 要するに (13) 式に (ω-√(k^2+m^2) ) を掛けて, となったところに, ω=√(k^2+m^2) を代入してやるととなるが,これに 2πi を掛ければいいのである. この式の中に出てくるというのは変数が乗っ取られる前の本来の意味での粒子のエネルギーであるので, と書き直すことができて,さらに次のようにまとめることができる. これは左回りの積分の公式を使った結果なので,これを -1 してやれば完了である. しかしまだ計算は全て終わったわけではない.次に $t_{1}-t_{2}<0$ だと仮定して同じことをやってやる.この場合には上半面での無限遠を通って左回り一周積分を考えてやることにすると都合が良い.つまり, ω=-√(k^2+m^2) の周りの左回り一周積分である.この場合にも先ほどと同じ公式が使える.要するに (13) 式に (ω+√(k^2+m^2) ) を掛けて, となったところに,を代入してやるととなるが,これに 2πi を掛ければいいのである. 今回もをで置き換えてやればいいが,左回り積分なので -1 を掛けてやる必要はない. しかしこのままでは分子にある二つの指数関数をまとめてやることが出来ない.そこで, k→-k という変数変換を行ってやる.そのようにしても結果が変わらないので問題ない.その結果として次のようにまとめることができるのである. これでようやく計算が終わりである. $t_{1}-t_{2}>0$ のときに (14) 式の形になり, $t_{1}-t_{2}<0$ のときに (15) 式の形になるのだから,これはまさしく (7) 式と同じものだ,というわけである.

積分コースの修正

さて,今の計算は特異点の近くでわずかに実軸から離れたコースで積分しているので,厳密には実軸上の積分だとは言えないのではないかという問題がある.そこで,(13) 式の代わりに次のような関数を考えてやる. すると,二つの特異点をわずかに実軸上から上下に逸らすことが出来る.

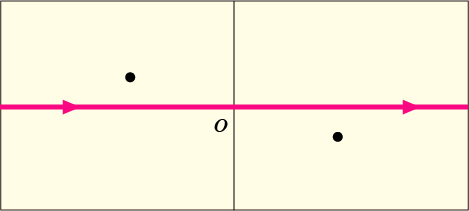
実軸上にあった特異点が上下にずれたので特異点を踏むことなしに実軸をまっすぐ進む積分経路を表す図

これなら実軸上を通る積分によって同じことが計算できて,最後に ε→0 としてやれば同じ結果になるではないか,という理屈で対処するのである.

しかし (16) 式のような変更によって本当に特異点は上の図のように移動するものだろうか？例えば,二つの特異点がそれぞれへ移動したと仮定すると,(16) 式の分母はとなるはずである.(16) 式と見比べるとととの間の関係はとなっているが,どちらも微小量であることに変わりはないので嘘をついているわけではなさそうだ.ただし,教科書では面倒臭がってとを同じ記号で表していたりするので注意が必要である.（実軸上からだけずれたかのように書いてある.）この辺りを疑うことなく読み解こうとすると結構混乱させられることになる.

ここらでキャンプしましょう！

軽く済ませるつもりだった寄り道が結構長くなってしまった.教科書ではすごく短く書いてあるのだが,ちゃんと丁寧に説明するとこれほどまでの長さを必要とするわけだ.つまづく人も多いところなので無駄な寄り道ではなかったと思う.

まだスカラー場の伝播関数の計算を終えただけであり,(2) 式の電磁場や (3) 式のスピノル場の伝播関数の計算が残っている.同じようなことをするだけなのでかなり説明を省いて進んで行けそうなのだが,何が起こるか分からないので念の為にここで一旦休憩しておくことにしよう.