流体の定義
液体や気体の運動を扱うのが「流体力学」である.液体も気体も,容器の形に合わせて容易に形を変えるという共通の性質を持っている.そこで液体と気体をひとまとめにして「流体」と呼び,それらに共通する性質を論じることにする.
ところで,容器に合わせて容易に形を変えるという点では砂粒や粉の集まりも同じ性質を持っている.しかしこれらは平らな地面に山盛りにしたときに山の形を維持するという性質があるため,流体とは区別し,「粉体(ふんたい)」あるいは「粉粒体(ふんりゅうたい)」と呼んで区別している.
こうなると,流体とは何かというのをきちんと定義しておきたくなってくる.粉粒体との根本的な違いはどこにあるのかというのが気になるし,流体力学というものがどのような前提条件で議論を始めようとしているのかという点もはっきりさせておきたい.
暗黙の仮定というものをなるべく排除しておけば,流体力学を現実の問題に当てはめようとするときにどんな条件を満たしていれば正しく成り立つのかというのを判断しやすくなるというものだ.とは言うものの,物理のほとんどの分野では,理論と現実との食い違いが生じてから暗黙の仮定の存在に気付いて理論を整備し直すものであったりする.
砂や粉を集めてやると山になって,力を加えない限りは勝手に崩れて行ったりしないが,水はわずかな重力でもすぐに平らにつぶれていきそうである.そこで「変形させるのに力が要らない物体」という定義にしてみたらどうかと考えてみよう.油やハチミツなどの粘り気の強い液体はしばらくは山盛りになるけれども,これらも時間が経てばそのうちに勝手に平らに崩れて行ってしまう.完全にどこまでも平らに薄っぺらに広がっては行かないが,それは表面張力の仕業であって,水でも同じことが起きる.表面張力はとりあえず無視しよう.
表面張力と粘性の関係が気になるって?関係ないらしいよ!こういうことも後で考えて行こう.
水や空気をイメージしている限りではこの定義で良さそうに思えるのだが,粘り気の強い液体を変形させるときには力が要りそうであるから,もう少し表現を変えた方が良さそうだ.「準静的に変形させるのに力が要らない物体」としたらどうだろうか.これは「限りなくゆっくりと変形させるならば力が要らない」という意味である.
ここで「ガラスは実は液体である」という話を思い出した.ガラスの分子は規則正しく並んでいるわけではなく,液体がそのまま固まったようなものであり,数千年,数万年スケールで見たらやがては溶け落ちるだろう,というのである.つまり,粘度が異常に高い液体だとみなせるというのである.時間スケールを変えて見てみればガラスさえ流体だという話に持っていきたかった.ところがガラスの結晶構造についてはまだ議論が続いており,近頃の研究によれば数千万年(!)スケールでも安定していられるだろうということになっているようである.この話はここではやめておいた方がいいだろう.そういうわけで,仕方なく別の例を使うことにしよう.
水ですら,急激な力に対してはコンクリートのような硬さを示すことが知られている.また氷ですら,ゆっくりと力を加えてやれば変形を起こす.このように,流体であるかどうかは実際の液体か固体かということとは別であって,考える時間スケールによって違ってくる話である.液体と気体をまとめて流体と呼ぶ,というのは分かりやすいが正確ではないということになる.
液体や気体の他に,プラズマもまた流体の一種である.プラズマについては「電磁流体」という呼び方をすることもあるが,プラズマだけを指す言葉ではない.電気伝導性を示す流体を「電磁流体」「磁気流体」などと呼ぶ.とりあえずは流体力学を普通に学んだ上で電磁気学の知識と組み合わせることで「電磁流体力学」となる.
さて,この定義でもまだ問題がある.圧縮しようとすれば水でも空気でも当然力が要るのだということを忘れていた.「変形させるのに力が要らない物体」と表現していたが,体積を変化させるような変形については除外してやらないといけない.
そこで,流体中の微小部分に掛かるであろう力を二つの方向に分けて考えることにする.仮に流体の微小な二つの部分の接触面があるかのようにイメージして,その面に垂直にかかる力「法線応力」と平行にかかる力「接線応力」に分けるのである.「接線応力」は「剪断応力(せんだんおうりょく)」とも呼ぶ.
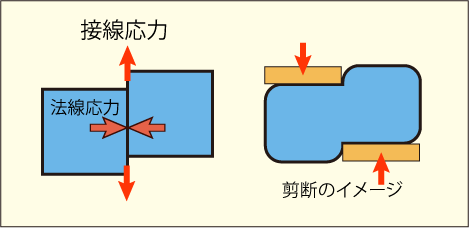
この図はおおまかなイメージを伝えるものなのであまり頼りにならないが,法線応力というのが二つの部分が互いに押し引きし合う力,接線応力というのが互いの部分が引きずり合うような力であると考えてほしい.剪断というのは右側の図のように力を掛けて物体を引きちぎるように切ることである.
法線応力の方は流体の定義に含めず,接線応力の方だけを定義の中で使うようにすればいい.
さあ,うまい表現にたどり着いたものだ.流体というのは右図のようにゆっくり剪断しようとしても無抵抗であって,少しも抗力を発生させないというのである.
しかし,もう少しだけ問題がある.流体が動いていると各部の速度の違いによって接線応力が発生する.要するに「粘性」のことである.粘性があっても流体だと認めてやりたいので,ここまでの定義を「静止状態」に限ることにする.準静的だと言っているのだからもうそれだけで静止状態を意味するのではないかと思うかもしれないが,今のままでは流れている流体の流路を準静的に変化させることが含まれてしまうので良くない.次のように表現するといいだろう.
さて,今度こそ問題ないだろうか?果たしてこの定義で充分だと言えるのだろうかと疑問を持った人がいるかもしれない.実はこの定義というのはこの後の記事で説明する予定の「パスカルの原理」の言い換えになっているのである.今回の話の進め方に少し強引さを感じた人は後ほどそちらも合わせて考えてみてほしい.
流体力学の全体像
この先,流体力学をどういう手順で説明して行ったら良いだろうか?流体力学が扱う話題をざっと分類してみよう.
まず,静止流体の話である.静止した流体中に沈んだ物体に働く圧力や浮力などを議論する.これらは基礎的な話として最初の章にでも突っ込んでおけばいいだろう.
そして,流体の中や表面に生じる波の話である.音波の話もここに含まれる.なるほど,そういう話は物理のどの分野で解説したらいいのかという迷いがあったが,流体力学の受け持ちであったのか.これは独立した章としてまとめることにしよう.
残りは流体そのものの流れの話,あるいは流体中を移動する物体の話である.移動する物体の視点に立てばその周囲を流体の方が流れていることになるわけだから,これらは結局は同じ話としてまとめることが出来るであろう.
流体が動く話は難易度に合わせてさらに幾つかに分けた方がよい.まず,粘性があるかないかで大きく難易度が変わる.粘性がない流体を「完全流体」あるいは「理想流体」と呼ぶ.一方,粘性がある流体を「粘性流体」「不完全流体」「実在流体」などと呼ぶ.
「実在流体」という用語は現実に存在する液体や気体のことを意味するので,粘性があるというだけでそう呼ぶのはちょっと避けた方が良いだろう.
もう一つ,難易度に影響する大きな要素は,圧力によって流体の体積が変化するかどうかである.体積が変化しなければ流体の密度を定数として扱えるので理論が楽になる.体積が変化しない流体を「非圧縮性流体」と呼び,変化してしまう流体のことを「圧縮性流体」と呼ぶ.
完全流体と言った時に「粘性無しで,かつ非圧縮性流体」のことを指す流儀の教科書もあるので注意が必要である.
分類の基準が沢山出てきてしまったが,まずは「非圧縮性の完全流体」だけで一つの章を用意するのが簡単で良いだろう.そして次に粘性だけを取り入れた「非圧縮性の粘性流体」の章を用意しよう.圧縮性流体については粘性の有る無しで二つに分けずに一つの章に入れてしまうことにしよう.
実在流体は厳密には圧縮性流体なのだが,流速が音速よりも十分に遅ければほとんど非圧縮性流体だとみなして問題ない.十分に遅いというのはどれくらいだろうか?例えば航空機の場合,マッハ 0.3 以下であれば非圧縮性流体の理論だけで充分であると言われている.大型旅客機の巡航速度はマッハ 0.8 くらいなのでこの範囲からは外れてしまう.それでも離着陸の時に限るならば問題ないだろう.
圧縮性流体の理論は「高速流体力学」や「空気力学」「気体力学」などの別名で呼ばれることがあり,超音速の航空機やガスタービンなどの話をするときにはどうしても必要になってくる.










