流体力学はニュートン力学である
流体力学はニュートン力学の応用である.ニュートン力学といえばという式であるが,流体の各部分は明確な形を持つわけではないし,連続したような存在であるから,このような方程式をそのまま当てはめて議論するのは難しい.それで幾つかの工夫をする.
まず「流体要素」と呼ばれる微小部分を考えて,そこに働く力を考えることにする.流体要素はその時々の議論に応じて考えやすい形を想定すればよい.決まった大きさがないのだから質量を使う代わりに密度
を使って議論する方が便利である.さらに力
を使う代わりに,単位面積あたりに垂直に働く力を考えるのが便利である.つまり,これは圧力である.流体の各部分は圧力によって加速したり減速したりする.流体力学では力ではなく圧力
が主役になるのである.
こういうわけで,流体力学に出てくる式は普通の力学に出てくる式とは見た目が大きく違って来てしまう.そのせいで流体力学が普通の力学と全く異なる学問であるかのような誤解を生んでしまうことがあるのだが,ニュートン力学を外れるようなことは何もしていない.
「流体力学を普通の力学のように考えるバカ発見www」みたいな,どっちがバカだよと言いたくなるような煽り文句が昔のネット掲示板のあちこちに貼られていたりしたものである.
とは言っても本来は原子や分子の動きを個々に追跡して出さないといけないはずの性質をサボって扱いやすくしているわけだから,どこかでおかしな仮定を紛れ込ませていないかしっかり監視しながら議論を続けていくことにしよう.
流体力学の限界
流体力学は原子や分子の動きを平均化して論じている.平均化しても問題ないと言えるためには,十分に多数の粒子が衝突を繰り返して,素早くエネルギーや運動量を分け合って均質化しているという仮定が必要である.この仮定は妥当だろうか?
粒子が多数あるかどうかの指標として,分子の「平均自由行程」というものが役に立つ.簡単に言えば,分子が他の分子に衝突しないで平均してどれくらいの長さを進めるかというものである.これは温度,圧力,分子の大きさによって決まるのだが,ここでの解説はやめておこう.
密度によっても決まると言えるが,それは圧力や温度で表せたりするから,どう表すかによって変わる.平均自由行程だけで一つの記事が書けそうだ.いつかチャレンジしてみよう.
この平均自由行程よりも十分に長い距離では,流体力学の仮定は成り立つだろうと言える.十分に長いというのは具体的にはどれくらいだろうか?そこで次のような「クヌーセン数」というものを定義しよう.
が平均自由行程で,
が流体力学を当てはめる範囲として想定している距離である.この値が小さければ小さいほど,流体力学にとって都合が良いということになる.およそ 0.01 以下ならば問題ないだろうということになっている.つまり,平均自由行程の 100 倍以上あればいいということだ.
真空に近い高高度の空気中や宇宙空間,あるいは,ミクロサイズの極めて小さな物体の周りの流れを考える際には流体力学の仮定が成り立たなくなってくる.前回の紹介からは漏れてしまったが,そのような状況について扱う「希薄気体力学」という分野も存在している.
流体力学の中心的な話を一通りやった後でそのような分野について調べて記事を書くのもいいかもしれないな.
水圧と気圧
今回は圧力の話に集中したかったのに,流体力学の前提について考えていたらいきなり脱線してしまった.元の話題に戻ろう.
流体一般で成り立つ話をしたいと思っているのだが,地球人の諸君にとっては水や空気を例にした方が身近で分かりやすいだろうから,そのようにしよう.水の中で受ける圧力を「水圧」と呼び,空気の中で受ける圧力を「気圧」と呼ぶ.
例えば,水中に深く潜れば潜るほど,より強い力を周辺の水から受けることになる.風呂に浸かるときにもそのような力が働いているのだが,あまり感じないのはちょっと不思議である.しかしゴム手袋やビニール手袋を付けて指先だけを湯船に浸してみれば,かなりの力で押されていることが実感できるであろう.ゴム手袋がなければビニール袋に腕を突っ込んで,袋に水が入らないように腕を突っ込んでもいい.
このような力は地球に働く重力が原因である.深いところにある水は,その地点より上にある水の重量分の力を支えている.つまり上から逃げ場なく押さえ付けられているのであり,同じ力で周囲の水を押そうとする.水の中に物体があれば,物体も同じ力で押されることになる.
ちょっと計算してみよう.水の中に途中までまっすぐ差し込まれたような円柱領域を考える.
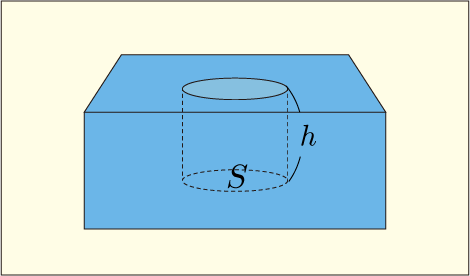
その底面の面積はだとしておこう.
の深さではその底面の上に
の体積の水が存在しており,密度を
だとすると全質量は
である.この質量に対して重力が働くから重力加速度
を掛けてやれば
という力で底面を押していることが分かる.これを底面積である
で割ってやると,圧力
は次のように表されることになる.
圧力の単位は
(パスカル)である.具体的な数値を入れてやれば,1 m 潜るたびに約 9.8 kPa ずつ水圧が増していくことが分かる.
残念ながら,気圧についてはこのような単純計算ができない.空気というのは圧力によって体積が大きく変化してしまうので,密度一定の物質として扱えないからである.上空へ行くほど大気は希薄になっていき,宇宙空間との明確な境い目も存在しない.それでも,気圧というのは自分より上にある空気の重さによって生じているという点では,水と同じ考えが当てはまる.
「地球の大気による圧力」というニュアンスを強く言い表したい場合には「大気圧(たいきあつ)」という表現も使われる.「気圧」と「大気圧」はほぼ同じ意味であると考えていい.厳密な定義などはないので文脈で判断すればいいだろう.例えば「気圧」の方は,地球大気の圧力の影響を受けないようにした密閉容器内の気体の圧力を表すのに使われたりもする.「大気圧」の方は別に地球の大気に限らない.地球外の惑星の大気の圧力を表すときに使ったりもする.というわけで,上では「空気の中で受ける圧力」だと書いたけれども特に気体の種類を空気に限ることもないのである.
絶対圧力とゲージ圧力
標高 0 メートルでの気圧は約 1013 hPa であるが,時間によっても場所によっても値が上下する.とは言っても,普段はおよそ 1 ~ 2 % くらいに収まる小さな変化である.なぜこのような変化が起きるかと言えば,太陽などによって空気が熱せられるせいである.暖かくなった空気は体積が増えるから密度が減って,上空までの空気の合計重量が軽くなり,その結果として気圧が下がる.逆に,冷えると密度が増して気圧は上がる.
これについてあれこれ書いていたら長くなってしまったので,別の記事で説明しようと思う.長くなった一番の原因は台風の話だ.気圧が 10 % ほども下がることもあるので無視できない現象だが,今は流体力学に集中したいので脱線するのはやめておこう.気象の話だけを集めた新たな章を用意することにした.
1013 hPa というのは 101.3 kPa であるから,実は 10 m ほど水に潜ったときに受ける水圧と同じだけの圧力を受けていることになる.水に潜ればこの空気の圧力を受けなくて済むかというと,そんなことはない.水の中では自分より上にある水の重みと空気の重みを合計したものから来る圧力を受けているのである.
ダイバーにとっては水面に浮上したときにちょうど 0 を示すように調整された圧力計を使うのが便利である.このような水圧の表し方を「ゲージ圧力」と呼ぶ.そして,空気からの圧力も含めて実際に掛かっている圧力は「絶対圧力」と呼ぶ.水面での気圧をだとすれば,水中の深さ
における絶対圧力は次のように表される.
(1) 式がゲージ圧力で (2) 式が絶対圧力である.科学的には絶対圧力の方が正しくて,実用的にはゲージ圧力を使うのが便利なのであるが,その違いはそれほど深刻ではない.水中のどの深さであろうとも,絶対圧力を知りたければゲージ圧力に一定値を加えるだけでいいからだ.多くの場面で必要なのは各点の圧力差であるから,どちらを使おうとも結果は同じになって不便はない.
絶対圧力,ゲージ圧力はそれぞれ「絶対圧」「ゲージ圧」という略した言い方で使われることもある.前者は丁寧な言い方にこだわる専門家風でかっこいいし,後者は現場で働くエンジニア風でこれまたかっこいい.
余計な要素を入れないで教える方が楽だということなのか,義務教育ではゲージ圧力を使って教えられるし,水圧はゲージ圧力で解答しないといけないことになっている.これが中学の頃の私にはどうにも納得いかなかった.本当に起きていることを無視して,テストの作法のために嘘を答えさせられているという気分になっていたのである.
もちろんそれは心情的に納得いかないというだけであって,からくりは理解していた.しかし正式にろくな説明もないまま強制させられるところに,世界が嘘で回っているかのような,自分だけが真実を知っているかのような憤りを感じていたのだった.
全方向に同じ圧力
流体の不思議な性質の一つとして,静止流体内の同じ地点であればどの方向からも同じ圧力を受けるというものがある.これも中学生の頃には少し納得が行かなかった.自分より上にあるものの重量を支えているのであれば,圧力は上下方向にだけ働いていても良さそうだからだ.
自分が何か比較的大きめのブロック状の固形物から成る山の中に生き埋めになったという不幸な状況を想像してみよう.

この場合,上から落下してこようとしているブロックの重みを支えることが出来れば助かる可能性がある.横にあるブロックがせり出してきて自分を押しつぶすようなことはない.上下だけに集中すればいいのである.
しかし流体の場合はそうはいかない.横からもせり出してくるかのような振る舞いをする.ブロックと違って自由な変形ができるから,上下につぶされるような力を受けた流体は水平方向へと変形しようとして,互いに横方向にも押そうとする.その結果,上下方向にも水平方向にも,同じ圧力で押し合おうとするのである.そればかりか,斜め方向にも,どんな角度であろうとも,同じ圧力で押し合うことになる.
水の中にある程度深く潜ったときには強力な水圧を受けているはずなのに,それでも人体が潰されないでいられるのは,全方向から圧力がかかっていて,縦方向だけにつぶされないで済むように均等に支えてくれているからなのだろう.同じ圧力でプレス機に挟まれればひとたまりもない.不思議な話だ.
なぜどの方向にも同じ圧力になるのだろうか?それを説明するために次のような図を使って説明しよう.
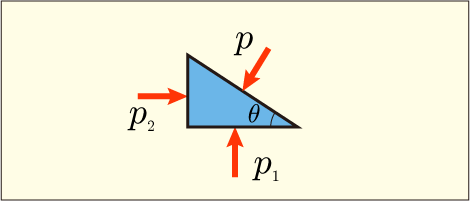
この三角の領域は微小な流体要素であって,今の説明に都合が良いような形に設定してある.奥行きを描くのは省いてあるが,倒れた三角柱のような感じになっていると考えてほしい.そしてその外側も流体である.
この底面にはという圧力が掛かり,側面には
という圧力が掛かり,斜面には
という圧力が掛かっている.それぞれの面に掛かる力を計算するためにはそれぞれの面積と圧力を掛ければいい.斜面の面積を
として表しておこう.
この三方向からの力は釣り合っているはずである.なぜなら,釣り合っていなければ流体要素が加速されて移動するはずであり,「この流体は静止している」という現在の仮定に反してしまうからである.
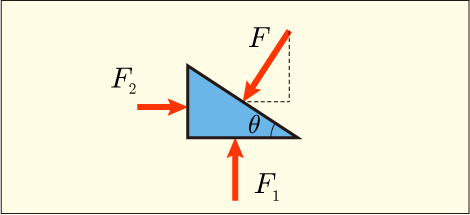
斜面に働く力を上下方向と水平方向に分解して釣り合いを考えてやることにしよう.まずは上下方向の力の釣り合いを使って関係を導いてみる.
水平方向も同様に.
底面の圧力
も側面の圧力
も斜面の圧力
に等しく,結局どれも等しいということが言えてしまう.しかもこれは角度に関係なく成り立つので,どんな向きの圧力であっても等しいということになる.
この説明で「面を垂直に押す力」しか考えなくて済んでいるのは,「静止流体では面に平行に働く接線応力が存在しない」というのを流体の定義として採用したからである.つまり,水以外の流体でも空気でも当然成り立つ話であると言える.
深さが違えば当然圧力の大きさは異なっているということに気を付けよう.上の説明では無限小の流体要素を考えたので,ほぼ一点で起きていることを表している.
パスカルの原理まで一気にやりたかったが思ったより長くなってしまった.今回はこれくらいにしておこう.










