流れはどうあるべきか
当然のことだが,この世界ではどんな流れ方でも自由に許されているわけではない.
前回の記事で描いた流れの図はいかにもそれらしく見えるように手作業でテキトウ,イイカゲンに作ったものである.おそらく現実の流れが従うべき規則を幾つも破っているだろう.どのように描いたらもっと本物っぽくなっただろうか?あの図の嘘が見破られるとしたら,どこがまずかっただろうか?
説明の分かりやすさのためには現実的な図を使うことが良いとは限らない.むしろデフォルメした方が言いたいことがよく伝わったりする.前回の図では,見て分かるほど派手に流れのベクトルの向きや大きさが変わって欲しかったし,しかし流線はあまり複雑にはなってほしくなかったので,どう描けば嘘くさくもなくバランスよく表現できるのかで悩んだのだった.
例えば次の図のような流れを仮定してそれについて考えてみよう.
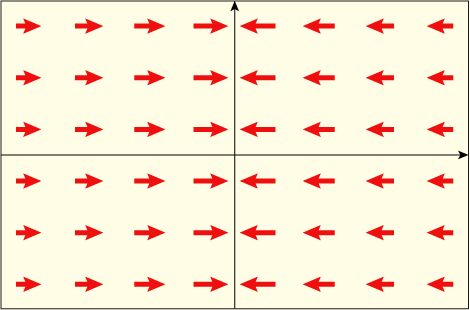
これは明らかにおかしいと分かる.左右から来た流れが中央でぶつかっているが,それがどこへ行くかが表されていない.流線を描こうとすると困るだろう.
もし 3 次元であれば,中央に達した流体はもうこの面上にはいられず,手前か奥へ向かって流れていかないとおかしい.もし 2 枚の板に挟まれた流体の 2 次元内での流れを表しているのだとすれば,中央付近にどんどん流体が集まってくることになり,密度がどんどん高くなっていくことだろう.そうでなければこのような流れは実現不可能である.そういうことがあれこれと分かる.
では実現可能な流れというのはどうあるべきだろうか?
前回は 3 つの「速度場の関数」を導入したのだった.
これらに制限を加えることで,現実に許された流れ方がどんなものであるかを見付けようというのが理論の目的である.その制限というのは何らかの方程式によって与えられることになるのだろう.
今,流体の密度が無限に大きくなってしまってそこが怪しいという話が出たので,まずはその辺りから制限を掛けてみることにしよう.
電磁気学を知っている人には簡単
まずは電磁気学を学んだことのある読者に向けて簡単に説明してしまおう.電磁気学には電荷の保存則を表す数式が出てくる.
この
というのは電流密度で,
というのが電荷密度を意味している.電流というのは電荷の流れであるから,電荷密度が減っていく場所では必ずそこから流れ出す電流があるし,電荷密度が増えていくところには必ず電流の流れ込みがあるという意味であった.
今回はこれと全く同じ考えを,電荷密度ではなく,流体の質量密度に対して当てはめようとしている.流体の流れが消え失せるところでは流体の密度が高くなるし,流体の密度が低くなっていくときにはそこからの流れ出しがあって,そのようにして全体では質量が保存しているはずである.
電流密度というのは電荷が単位時間に単位面積を通過する量を意味していた.電荷密度とその速度を掛ければ電流密度になる.
それと全く同じイメージで,電荷密度
としていたものを,流体の質量密度
として解釈し直してみよう.質量密度
とその場所の流れの速度
を掛ければ,単位時間に単位面積を通過する質量を意味することになる.それを「質量の流れの密度」と解釈して電流密度
の代わりに当てはめる.つまり,流体力学では「質量保存則」として次のような式を考えればいいことになる.
これを「オイラーの連続の式」「流体の連続方程式」などと呼ぶ.なぜ連続というのか,少し不思議な気もする.おそらくは「流れが理由なく突然消えることがなくて,大抵の場合はちゃんと繋がっている」というニュアンスなのだろう.
もし圧力を掛けても流体の密度が全く変化しないような「非圧縮性流体」について考えたい場合にはこの右辺は 0 であるし,左辺にあるも場所に関係なく同じ値のままなのだから定数とみなして括弧の外に出してもよくて,次のようなとても簡単な式になる.
しかしこういう単純化した式は後で具体的なことを考える時に,計算を楽にするために仕方なく使うものである.その時が来るまでは,本質的には (1) 式が成り立っていると考えておくのがいいだろう.
今回の話はこれでほとんど終了である.このあとの話はざっと読み飛ばして,一番最後の方だけ読んで次へ進んでもらえばいいだろう.
電磁気学をまだ学んでいない人向けの説明
さて,お待たせした.まだ電磁気学を学んだことのない人も安心して欲しい.
今の話に出てきた (1) 式と同じものを,電磁気学の知識を前提としないで 1 から説明し直そうと思う.とは何なのかという話もしないといけないし,偏微分の説明もしないといけないので,説明する私もそれを聞く側もちょっと大変かもしれないが,頑張って付いてきて欲しい.これを理解すれば後で電磁気学を学ぶときにも楽になる.
まずはの定義から話しておきたい.これ自体は流体力学の物理的内容とは全く関係ないので,余計な考えが混じらないようにしておきたい.説明のためだけに流体力学とは全く関係のない何らかのベクトルを用意して
という記号で表すことにしよう.このベクトル
は場所と時間で決まる関数となっている.つまりその成分はそれぞれ次のような関数であるとする.
このとき,
というのは次のような計算内容を意味するのだと定義する.
ここに出てくる
などの記号は「偏微分(へんびぶん)」と呼ばれているもので,多変数関数を微分するときに使われる記号である.他の変数は全て定数だと思って,一つの変数だけで普通に微分すればいい.
なぜこの計算内容をなどと略記するかと言うと,これが特別な意味を持つからである.
というのは「divergence」の略で,日本語でもカタカナ読みで「ダイバージェンス」と呼ぶ.意訳して「発散」と呼ぶこともある.しかしイメージとしては発散よりも「湧き出し」に近い.
(2) 式の定義を見て分かるように,このというのはもはやベクトルではなくスカラーである.つまり何らかの一つの関数のようなものであり,その変数は
である.言い換えれば,場所と時間によって決まる何らかの値であり,その値は正にも負にも 0 にもなり得る.その数値の意味をこれから説明しよう.
空間のある場所に,各辺の長さが,
,
であるような微小な直方体領域を想像してみてほしい.その直方体の体積
は次のように表すことが出来る.
これを
と掛け合わせると次のようになる.
とりあえず,この右辺の第 1 項だけ取り出してその意味を考えてみよう.
はベクトル
の
成分である
の
方向についての変化率を表しており,これに
をかけた量
は
方向に
だけ移動する間の
の増加量を表している.残りの
というのは微小な直方体の
面の面積を意味している.この項は,この
面の面積に比例するような量でもあるというイメージが大切だ.
つまり第 1 項は,微小な直方体の面から
方向に向かって入ったベクトルが,この直方体の中を通り抜ける間にどれだけ増加するかを表しているということになる.
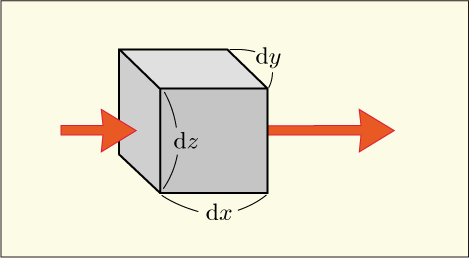
この図ではベクトルが右を向いている場合を描いているが,ベクトルが左を向いている場合にも同じことが成り立つ.
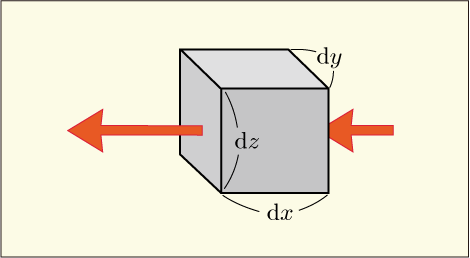
この図のように直方体の右から左に向かってベクトルが入るということは,この付近ではの値がマイナスになっているということである.このベクトルの長さが大きくなって直方体の左から出て来るということは
だけ進む間に
の値が減少したということである.これは逆に見れば
進む間に
の値が増加したということであり,(3) 式のような計算をしたときに,このような状況でもプラスの値として出てくることになるだろう.
つまり (3) 式の第 1 項は直方体の中から新たに増えて出てきたの量を表すことになる.
他の項も同じイメージが成り立つ.第 2 項は同じことが成分でも成り立っていることを意味しており,第 3 項は
成分でも成り立っていることを意味している.
つまりというのは絵的に見たのと全く同じような意味で,ベクトルが直方体の中から湧き出してきた総量を表すようになっているのである.もしマイナスの値なら,この直方体の中に吸い込まれて消えてしまったのだろう.
(3) 式の右辺のどれかの項がマイナスでも,他の項がプラスになっていて,全体として値が 0 になっているということもあるだろう.その場合にはこの箱の中に入っていったベクトルは増えも減りもせず別方向へ進路を変えて出ていったというイメージが成り立つ.
では (3) 式からを外した
単独での意味というのはどうなるだろうか?その地点の微小領域から「湧き出し」てくるベクトルの量を単位体積あたりの量として換算した値だという解釈ができそうである.
ここまで分かればについての理解はもう完璧である.
お疲れ様!ここでちょっと休憩してもいいです.この長い説明を忍耐強く読んで新しい理解を手に入れた自分を褒めて乾杯してきて下さい!
流れに当てはめて式を作る
の意味が理解できたので,ここから (1) 式を作るのは簡単である.先ほどの「電磁気学を知っている人」向けに話した説明が理解できるようになっているだろう.しかし念の為,丁寧に説明を続けよう.
それぞれの地点での流体の密度と,同じ地点での流体の速度を掛ければ,流体の物質が流れていく量が表せる.
密度
はベクトルではなく,
だけがベクトルであるから,これは全体としてはベクトルである.具体的には次のような成分を持つベクトルである.
これを先ほどまでの説明で使っていた
の代わりに (2) 式に代入してやれば,その流れが現れたり消えたりする量を表す表現が得られることになる.
我々の日常で質量が勝手に現れたり消えたりすることはないので,
が 0 以外の何らかの値を持つ地点では流れが増えたり減ったりしているだけである.代わりに物質がその辺りから流れ出したり,その辺りに溜まったりして,密度が減ったり増えたりしているのであろう.そのように考えて次のような式が作られることになる.
こうして (1) 式が作られたわけである.
流れのイメージ
ところで,流体の密度と速度
を掛けたものが質量の流れを表しているという考え方がすぐに理解できなくて苦しんでいるかもしれない.イメージしやすくするために,速度が
方向を向いていることにして考えてみよう.微小な体積
内に含まれる微小な質量を
と表すとすると,密度
というのは次のように表せる.
そして,この微小な体積内にあった質量
が
方向へ
だけ移動して,
面を通って全部出ていったとしよう.その過程に微小時間
だけ掛かったとすると,このときの速度は次のように表せる.
これらを掛け合わせると次のようになる.
つまり,微小な時間
内に,
面の微小な面積
を通って微小な質量
が移動したときの比率という意味だ.かっこよく言い直せば,「単位時間あたりに単位面積を通りすぎる質量」だということになる.
というのはそのような「単位時間あたりの流れの通過量」である
が微小な箱の表面を通して出入りするときの,単位体積あたりの増減量を意味していたので,それが単位体積あたりの質量の時間変化(つまり密度の時間変化)と直接イコールで結んでやって問題ないということになる.このように隅々まで解釈がぴったりうまくいく.(1) 式が単なる雰囲気だけでテキトーに組み合わせて作られたようなものではないことが分かるであろう.
もう少し数学寄りの説明
ここまでの説明が手持ちの教科書とは全く違った雰囲気なので,信用していいものかどうか迷っている人もいるだろう.だいたい,分厚い流体力学の教科書を書く人というのは数学が得意なので,数学の定理をさらっと使って説明を終えてしまう方が好きなのである.
念の為に同じ内容をそのような方法でも説明しておこう.
先ほどまでの説明とは違って,今回は微小体積ではなく,かなり広くて自由な形をした閉じられた領域を想像してみてほしい.そのような領域内の全体で密度を積分してやれば領域内に存在する流体の全質量
が計算できる.
質量は保存するので,この質量が変化するとしたら,この領域の表面を通して質量が出入りする場合に限られるだろう.しかも出入りするということは,この表面に対して垂直な速度成分を持つ場合に限られるだろう.そこで,領域表面に微小な面積
の平面があると考えてみる.その面の外向きの法線ベクトルを
とすれば,流体がその面に向かう速度成分は
と表されるだろう.この速さで
の面積を通過するのだから,単位時間あたりに
という微小体積内にあった流体が移動したことになる.その質量は
と書けるだろう.これを領域の全ての表面に渡って足し合わせてやると次のようになる.
法線ベクトルを外向きにして考えているので,これは出ていく量を表している.ここまでの話をまとめると次のように表せるだろう.
この最後のところで微分と積分の順序を入れ替えてしまっているが,物理学者が何も気にせずお気楽によくやってしまう式変形である.数学者が見ればギョッとするだろう.この等式が成り立つためには本当は細かい証明が要るのだが,積分範囲が有限で
が連続で微分可能であれば成り立つらしいので問題ない.
物質は原子から出来ているのだから密度ρが連続関数であって微分可能というのも嘘なのだが,流体力学で使っている密度という概念がその辺りの原子の存在を平均化したものとして連続関数であるかのように使っているのだから,そういう扱いをしている限りは問題ないのである.
ところで,「ガウスの定理」と呼ばれる数学上の定理があり,次のような等式が成り立つことが言える.
領域の表面全体に渡る積分を,領域の体積全体の積分へと変換する公式だと理解して欲しい.慣れていないと面倒くさそうな式に見えるが,先ほどの
のイメージを理解していれば簡単である.右辺にある
は微小体積あたりの湧き出し量を表しているのだった.それを積分するということは,領域内を微小な直方体でびっしり埋めてやって,その全てから出てくる値を合計したことに相当する.一つの微小な直方体からのプラスの湧き出しはすぐ隣の直方体に入るのでマイナスとして計上されるだろう.そのように考えていくと,領域内部での値はあったとしても全て相殺されてしまって,結局は領域の表面からの出入りだけを計上してやれば同じ計算をしたことになる.それがこの式の意味だ.
この「ガウスの定理」を (4) 式の左辺に適用してやると次のような式になる.
この両辺は積分範囲も同じであり,ここまでの話はどんな形の領域を考えても成り立つのだから,被積分関数どうしが等しいと考えていいであろう.そのように考えて中身を取り出せば次のようになる.
こういう考え方でも (1) 式と同じになるというわけである.
説明の雰囲気が違うだけであって,先ほどからやっていることは全く同じである.
方程式が足りていない
さて,流体の速度を表す関数に現実的な制限を加えようとして (1) 式のような条件式をとりあえず一つ用意してみたのに,その式の中には密度を表す関数
が入ってしまっている.求めるべき未知関数が 4 つに増えてしまった!
流体力学の理論は,流体の各部の速度だけを考えるような形式には収まりそうもないということだ.
これら 4 つの未知関数はまだ自由すぎて現実の振る舞いから外れている状況も許されてしまうだろう.さらに別の方程式を使って制限をかけてやらないといけない.一体,この理論は最終的にどんな形でまとまることになるのだろうか?
次回,さらに追加される方程式に,乞うご期待!










