一番知りたいのは流体の速度である
そろそろ動きのある流体の話に入って行こうと思う.
しかしどういう形式の理論を作っていけばいいのだろうか?流体力学に何を期待するのかということから考えていくといいのかもしれない.漠然とした目的としては,流体がどう流れるかを知りたいのである.
すると各地点での流体の速度が分かればいいことになる.これらは場所によって値が違っているだろうし,時間によっても変化していくのだろうから
という形の 3 つの関数として表されることになる.イメージとしては次の図のように各点各点に速度を表すベクトルがぎっしり並んでいる様子を思い描くといいだろう.
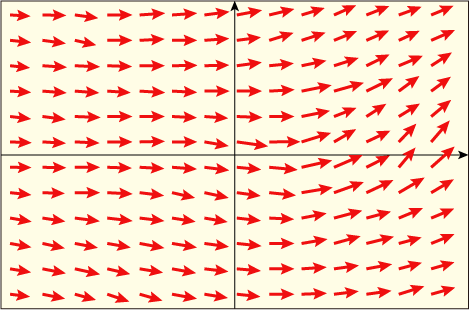
図があまりごちゃごちゃしないように平面だけで表しているが,実際は 3 次元空間に矢印がびっしり並ぶようなイメージである.これらの速度ベクトルはもちろん時間によって変化してもいい.
物理では,位置と時間の関数として表される物理量を「場」と呼ぶのである.「電場」や「磁場」や「重力場」などと同じで,その物理量があたかも空間の性質であるかのように取り扱う.今回のこれは流体の速度を場の形で表したものなので「速度場」と呼ぶ.
流線
この速度場のベクトルの矢印を繋いで行って出来る曲線のことを「流線(りゅうせん)」と呼ぶ.
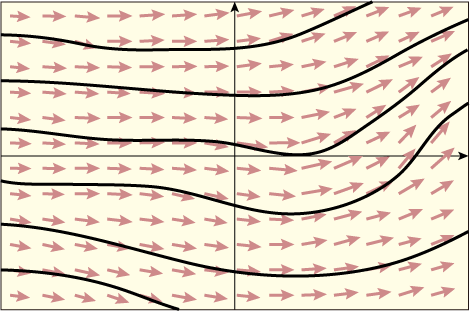
しかし雑に繋いだのでは正しい流線にはならない.矢印どうしは先ほどの図のように離れた形で存在しているのではなく,一つの矢印から無限小だけ離れたすぐ横には別の矢印がある.そこではもう矢印の方向が変化している可能性があるからである.実際,最初の図のようなまばらに置かれた矢印だけからこの図のような流線は再現できない.矢印どうしの間隔を十分に密にして描いた上でそれらを繋いでいけば,密にすればするほど正しい流線に近付いていくだろう.
だから正確に言おうとすれば次のような表現をした方がいいだろう.流線とは「各地点での接線が速度ベクトルの向きに等しくなるように引いた曲線」のことである.まだ分かりにくいな.こう言い直そう.
注意してほしいのは,流体はこの流線の通りに流れるわけではないという点である.いや,もし速度場が時間的に少しも変化しないのなら,流体は流線の通りに流れると考えてもいいだろう.しかし時間的に変化する場合には,途中で次々とコースチェンジが起こるようなものだから,各点にある流体は流線の通りに流れてきたわけではないし,その後も流線の通りに流れていくという保証がない.
流体の辿ってきたコースや,これから辿るであろうコースのことを言いたいときには「流跡(りゅうせき)」あるいは「流跡線(りゅうせきせん)」という用語を使う.
今井功の有名な教科書では「流跡」ではなく「みちすじ」という言葉を使っている.英語ではどちらも path line である.ちなみに「流線」の方は英語で streamline である.似たイメージの英単語だらけで大変である.
ところで「流線形」は英語でどう言うのだろうか?調べると streamlined という単語が出てくる.これは「流線形の」と言いたいときや,「(ある物体が)流線形になっている」と言いたい時に使うものであろう.あえて名詞として「流線形」と言いたいときには streamlined shape などと言えばいいのであろう.
流脈
さて,今の話題には関係ないのでここで説明すべきか迷うのだが,「流跡」に似た概念として「流脈(りゅうみゃく)」あるいは「流脈線(りゅうみゃくせん)」というものがある.流脈とは,ある固定した点にインクを流し続けたときに,流れに乗ってインクが描いていく線のことである.軽く説明を聞き流していると,流跡と流脈は同じなのではないかと勘違いしてしまうので,気をつけて考えてみて欲しい.
流脈線は煙突から出た煙が風に流されて描く線だという例えもよく使われる.
流れの方向が時間によって変化する場合には,流跡と流脈はそれぞれ全く違う線を描く結果になるのである.すぐに分からなくても気にしなくてもいい.まぁパズルのようなものである.
ヒントが要る?
流跡線の方は一度引かれてしまえば変化しないが,流脈線の方は,途中の線の全体が流れの上に乗ったまま移動し続けるという違いがあることに注意を向けよう.
流脈線は英語で streakline なのだそうだ.綴りが似ている単語で驚いた.
オイラーの方法とラグランジュの方法
ここまでに説明したような速度場を中心にして理論を作っていく流儀のことを「オイラーの方法」と呼ぶ.「オイラー流」と呼びたいところだが,流体力学の中でこの表現を使うと何かの特別な流れ方を意味しているのではないかと誤解されてしまう可能性があるので表現に気を付けている.
「オイラー法」だとか「オイラー型の理論」だとか呼ぶこともあるが,別の分野に同じ呼ばれ方をしているものがあったりしてなかなか気を使う.
一方,流体が実際に進むコースである「流跡」にこだわった形で理論を作っていく流儀のことを「ラグランジュの方法」と呼ぶ.ある時点に,ある場所にあった流体が,今後どの位置に移動していくかというのを関数として表して追跡していく形である.
具体的な形を少し見ておいた方が分かりやすいだろう.例えばにおけるある流体の位置が
だったとすると,それが
秒後にたどり着く位置を次のような 3 つの関数で表すことになる.
ラグランジュの方法は数学的に多少ややこしいことになるのだが,「ラグランジュの渦定理」などを導くときに必要になる.必要になったところで説明を始めることにしよう.
必要でなくても基本的な話が一段落したら説明を始めるかもしれない.
現在の主流は「オイラーの方法」なので安心して欲しい.そちらの方が流れの全体を見渡しているようなイメージで話ができるし,コンピュータを使った流れのシミュレーションなどの実用的な面でも便利なのである.
もちろんどちらの流儀を使っても同じ結論が導き出せるわけだが,場面によって得意不得意がある.教科書によっては断りなくどちらの視点も混ぜながら説明したりするので,初学者は混乱してしまいがちになる.私としては,できるなら完全に分けて話をしたいと思っているが,どれくらいきれいに分けて話せるものなのか,まだ全体を見渡せていないので判断がつかない.
物体と流体、どちらを動かす?
ここまでに説明した「オイラーの方法」は流体が移動するという考え方であった.固定した配管の中を通る流れや,静止した固い物体の周囲を通り過ぎていく流れを考える場合には何の問題もないだろう.しかし「静止していた流体」の中を固い物体の方が移動していく場合にはどうだろうか?
それは相対的には,静止している固体の周囲を流体が動いていると考えても同じであろう.飛行機や車などの周りの空気の流れを見るために「風洞実験」というものが行われる.物体を固定しておいて,そこに送風機を使って均一な速度の風を送ることで,車や飛行機が進んでいるときの様子と同じ状況を再現するのである.
なるほど,オイラーの方法でも問題なく議論できそうだ.
しかしこれにも限界があるのではないだろうか?物体が等速運動をしている状況は再現できるのだが,加速中の物体の周りの流れの再現が難しい.風洞実験では,既に送風機を出てしまったあとの空気を一斉に加速することはできないからである.実験としては困難があるが,理論的になら回避できるかもしれない.物体は相変わらず固定しておいて,流体に謎の外力を働かせて一様に加速するといった工夫をすれば同じ状況になりそうだ.
流体力学はどこまで現実を表せるだろうか?
そういう問題があれこれ出てくるとしても,あまり心配する必要はない.というのも,流体力学はそもそも難しいのである.たとえ理論的な基礎方程式や定理などがしっかり立てられたとしても,あらゆる問題を解決できるわけではない.具体的な問題を解くには様々な工夫が要る.教科書では「この問題についてはこういう仮定を入れることで何とかしてそれらしい答えを得ることができました!」という成功事例がたくさん紹介されている.
例えば,水と油の境界で密度が不連続的に変わるような場合に微分可能ではなくなってしまってそのままでは理論が当てはめられなくなるけれど,難点をうまくすり抜けるための考え方を用意しました,だとか.水中の泡のように常に物体の形が変わるような場合についても理論を当てはめる考え方を工夫しました,だとか.流れが速すぎて現実には真空が発生してしまうので,そのような状況を表す条件を人為的に加えて解くことにします,だとか.普通の方法では解けそうにもないけれど,高次元の問題に置き換えて何とか乗り越えました,だとか.
さらに言えば,現実の問題は一種類の流体の流れだけを考えて済むようなものでもない.例えば気象のシミュレーションをしようと思ったら,単純な空気の流れだけではなく,上下方向の重力,空気の湿り気,水蒸気の流れ,熱の移動,コリオリ力なども考慮に入れなければならない.
このように,解決せねばならない現実の問題はいっぱいあるし,それらと戦うための理論的な武器が次々と説明されて教科書は分厚くなっていく.私としてはそういう細かい個々の話はできるだけ後回しにして,最小の道具でどこまで遠くまで見渡せるようになるか,というチャレンジをしてみたいのである.
分かった気にさせるだけの速習コースだという批判はあるだろうが,まさにそれが必要だという人は多いだろうし,そういう人たちに届けたいと思っている.
要するに,あらかじめ色んな場合についての心配をして,万能な方法ではないではないかなどと嘆いても無駄だし,それらに対して少しくらい解決したところでそれは問題のほんの一部でしかないということである.出来るところから理解していくことにしよう.











実在の流れとは一切関係ありません。