詐欺は良くない
この第 2 部では次のような単純な 2 つの式だけを基にして話を進めて行くのだと書いた.
しかしこのような表現をするたびに,少し詐欺臭いというか,申し訳なさを感じてしまうのである.(1) 式は具体的に書けばそれほど簡単でもないし,(2) 式はアインシュタインの縮約記法を使っているから,展開してやるともう少し項が多い.しかも (2) 式は 3 つの成分をまとめて一つにして書いたものである.そういうわけで,実際には上のような 2 つの式ではなく次のような 4 つの式なのである.
ただし,重力は
軸の負の方向に働いていると考えて,
として表してみた.初めて学ぶ人に向けては,この形の式をちゃんと見せておきたかったのである.
さあ,単純な式だからこれを解け!と言われてもそれほど簡単なことではない.これから立ち向かう相手の正しい姿をよく見て,読者にも覚悟してもらうことが必要だ.
次元を減らしてみる
上では 4 つの式だと書いたけれども状況によっては式の数が減らせる.例えば二枚の平行な板で挟まれたごく狭い隙間の流れを考える場合だ.その板を水平に寝かせて置くか,屏風のように縦置きにするかによって重力の掛かり方が違うわけだが,ここではひとまず寝かせて置いて軸方向に重力が掛かっていることにしてみよう.
上下方向への流体の移動はほとんど制限されているのでとしてもよいだろう.すると色んな項が消え失せてくれて (3) ~ (6) 式は次のようになる.
この中でも (10) 式 はひときわ単純だ.これを整理すると次のようになる.
これは簡単に解けて,解は次のような形になる.
右辺の
は
と
のみに依存する任意関数である.この解の意味は難しくはない.何らかの別の条件によって
が決まるが,それ以外に重力による水圧あるいは気圧のようなものが掛かっていて,
軸の負の方向,つまり下方に行くほど圧力
が少しだけ高いという状況を表しているだけである.今の状況設定ではそれほど深さというか厚みはないので,そのような静水圧のようなものをあまり気にするほどではない.
でははどうやって決まるかというと,(12) 式を (8) 式や (9) 式に代入すればいいのである.その結果として (12) 式の
の項は消えてしまうだろう.結局は (8) 式や (9) 式の右辺にある
のところが
に置き変わるだけなので,改めて
を
という記号で書き直せば,元の (8) 式や (9) 式のままである.こういうわけで,(10) 式のことは忘れてもらっても良くて,解くべきは (7) ~ (9) 式の実質 3 つの式で済む.
屏風のように立ててみる
今の二枚の板を立てて設置してみた場合のこともちょっと気になる.重力は相変わらず軸の負の方向を向いていると仮定しよう.板の法線の向きを
軸にすれば,今度は
となっている.それで (3) ~ (6) 式は次のような式になる.
(15) 式は
軸方向に移動しても
の値が変化しないことを表しているだけの式なので無視して構わない.そういうわけで,(13) (14) (16) 式の 3 つがこの状況の方程式だということになる.
この式は飛行機の翼の断面を考えるときにも使える.軸方向に向けて長く伸びた形の翼の場合,
軸方向に移動しても翼の断面の形状や大きさがほとんど変わらないだろう.このようなときには空気は
軸方向にはほとんど移動しないので
面内だけでの空気の流れを考えればいいのである.
ここで説明したような構造の「流れの実験観測装置」が実際にある.「乱流屏風」と呼ばれていて,それはそれはもう美しい実験だというので少し前に世間の話題になった.装置の詳細についてはこのリンク先の「科学コミュニケーターブログ」内の解説が詳しい.二枚の板の隙間はわずか 5 mm で,その間に流体を流して観測するのである.
1 次元も試してみる
2 次元的な流れを表す式は 3 次元の場合よりずっと簡単になった.すると,1 次元の場合にはどれくらい簡単になるだろうかという興味がわいてくる.かつ
としてみれば良いだろう.面倒だから重力は省いて考えてみよう.とりあえず,次のような形になるであろう.
(17) 式から言えるのは,場所による速度の違いがないということであり,つまりどの地点でも速度が同じだということである.そのような解しか許されないのは当然である.今考えている流体は圧縮されることがない.どの部分の流体も
方向や
方向へは少しも移動しないで同じ方向へ移動するのだから,どこにも逃げ場がない.移動した先に元々あった流体も同じだけ前に進まなければ困るだろう.まったく面白味のない解である.
(18) 式は (17) 式の条件を代入してやることでさらに単純になる.
全域で同じ速度でありながら,時間的に速度が変化することは許されるようである.ということは,全域で全く同じように加速しなければならない.加速の原因となっている力は圧力の勾配であるから,それが全域で同じでなければならないだろう.このようにして,圧力の分布も単純な形しか許されないことになる.
そのような解が現実的であるかどうかはさておき,これ以外の現象は起こりそうにもないし,単純すぎて面白くない話である.1 次元についてはほとんど全く考える意味がない.
そういうわけで,なるべく簡単な式を使うのが好きだという人は 2 次元の流れを考えるのがいいだろう.コンピュータにシミュレーションさせる上でも一番負荷が少ないもっとも単純な式である.
ちょっと違うけど 1 次元
ところで,1 次元的な流れの例として次のような説明図が出てくることがよくある.
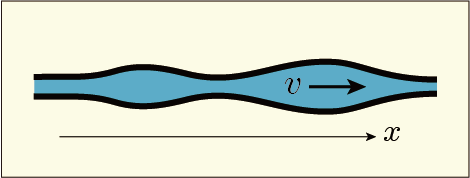
パイプの中を流体が流れていると思ってほしい.この状況では流体はパイプに従って一方向に流れるしかないし,各点での流れの速度はパイプに沿って測った距離の関数として
と表されるし,各点での断面積も
のように表されることになる.まさに 1 次元的である.
しかしこのような状況の場合,流体の速度は場所によって異なることが許される.断面積に変化があるので,パイプに沿った方向以外を向いた流れもパイプ内のあちこちに存在しているからだ.しかしそのようなものを無視して,パイプの向きに沿った速度だけを使って説明しているのである.そういう説明が出てくることはよくある.
このようなわけで,この図のような状況は厳密な 1 次元の流れではなく,先ほど式を使って説明した 1 次元の流れとは全く別の話なのである.しかし私自身も少し混乱していた.先ほどの (17) 式を見たときにこのような説明図のことを思い浮かべてしまって「速度が全域で一定だという結論はおかしくないか?」などとしばらく迷ったのである.私以外にも同じことで引っ掛かる人がいるかもしれないと思ってこの話を付け加えておくことにした.










