流体力学：応力テンソル

ことの経緯

前回の話でいきなり応力テンソルというものを紹介して,ほとんど説明なしに使ったのだった.スッキリしない部分があったと思うので,今回はその補足としてもう少し詳しく説明しておこうと思う.

応力テンソルというのは流体力学だけで使うわけではなく,様々な物体内部に掛かる力について広く使える道具である.それで,しばらくは流体ではなく固形の物体を想像しながら読んでもらったほうがいいだろう.今回は応力テンソルとは何かということに集中するので流体の話はしないかもしれない.

流体力学に必要だからという理由だけであらかじめ学んでおくのはつらいかもしれないが,もう既にどこでどう使うのかが分かったと思うので少しは興味も出てきているだろう.

では,説明を始めよう.

応力の種類

応力というのは簡単に言えば物体内部に掛かっている力のことである.物体を両側から押せば圧力が発生するし,両側から引っ張ってやれば,ちぎれまいとして耐える力が発生するし,ねじろうとすればねじ切れるのに耐えようとする力が発生する.それらを総称したものが「応力」である.

応力の種類を分類するためには,物体内部に断面を設定すると分かりやすい.断面の法線方向に断面を押したり引いたりするように働く力を「法線応力」と呼び,接線方向に断面をずらすように働く力を「接線応力」と呼ぶ.

法線応力は別名「垂直応力」とも呼ぶ.また,接線応力は別名「ずれ応力」「ずり応力」「剪断応力（せんだんおうりょく）」とも呼ぶ.

剪断の「剪」という字が常用漢字ではないという理由で「せん断応力」という表記が行われることの方が多い.工業規格などの公文書がどれもそうなっているから,特に工学系分野ではこのようなルールに従う傾向が強いのだろう.

こういうことを言うと,じゃあ理学系分野ではどうなんだということになるのだが,結構ややこしい.常用漢字ではないからというので変更された用語はあれこれある.「函数→関数」「共軛→共役」など,同じ音のあまり意味のない漢字で置き換えられたりしている.「輻射→放射」のように徐々に変わっていった例もある.「伝播→伝搬」については電波法で使われているので電波工学では「伝搬」の方をよく使うが,数学や物理ではそれはおかしいだろと抵抗して「伝播」を使い続けている方が多い.
進歩の激しい化学・生物・医学分野では古い用語自体が時代遅れの概念だからといって使われなくなっていったり,全く新しい用語に置き換えられることの方が目立っている.
そういえば最近,テレビや新聞では「隕石」を「いん石」と書いているのだなぁと気付いた.

法線応力はさらに 2 つに分類される.断面を両側から押すような力を「圧力」あるいは「圧縮応力」と呼ぶ.そして断面を両側から引っ張るような力を「引っ張り応力」と呼ぶ.

このように色々な用語が存在しているが,考えている断面を垂直に押すか,引くか,平行にずらすかという 3 通りしかないので,まとめてみると意外と単純である.

応力	法線応力（垂直応力）	圧力（圧縮応力）
		引っ張り応力
	接線応力（ずれ応力）（ずり応力）（剪断応力）（せん断応力）

この表の赤字はこの解説で主に使う用語で,カッコ内は様々な業界や分野で使われることのある別名である.

物理ではこれらの力をどれも「断面の単位面積あたりの力」として表すことにしている.機械工学,材料工学でもこれと同じ習慣を採用しており,応力と言えば単位面積あたりの力である.

しかし土木・建築関係では,単位面積あたりの力を「応力度」と呼んでおり,ただ「応力」と言ったときには面積で割らない普通の力のことを意味している,という慣習の違いがある.

さて,ここまでの用語は全て断面上の一点に掛かる力についての分類であった.これらの他に「ねじり応力」という用語もあるが,これは断面上のそれぞれの場所で異なる接線応力が働いている状況のことを表しているので,少し高次の概念である.物体全体をねじるように力を加えた場合には,そのような状況になったりする.しかし今回は断面上の一点に掛かる応力の表し方について話そうとしており,「ねじり応力」は取り扱わないことにする.

どう表せばいいのか

さて,応力の分類は出来たのだが,まだ少し問題がある.想定する断面をどういう向きに取るのが正解なのだろうか？

想定する断面の向きを変えれば,法線応力だと思っていたものが接線応力として働いていたりするだろう.

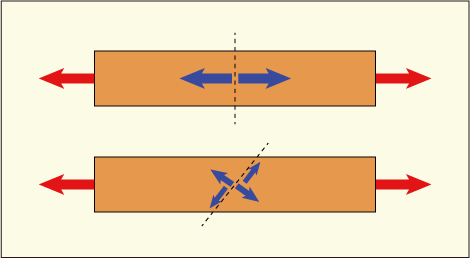
物体を左右から引っ張った場合に,垂直な断面を考えれば法線応力しか存在していないが,斜めにした断面を考えれば,断面をずらすような力も掛かっていることになる.

上の図のような場合には垂直な断面を考えるのが最もシンプルだと言えるだろう.しかし次のような場合はどうだろうか？

物体を左右から押し,上下からも押したとき,考えるべき断面をどう選んだらこの物体内に発生している応力を最も単純に表せるだろうか？圧力が斜めに働いていると考えられるかもしれないが,かと言って斜めの断面を考えようとすると接線応力も発生していることになって余計にややこしいだろう.

あまりそういうことで悩んでも仕方がない.どの面を考えるかというのと,その面にどんな応力が働いているかというのはワンセットの情報なのである.

しかしいちいち断面を指定してからでないと応力を表すことが出来ないというのは不便で居心地が悪い.断面の選び方に関係なく,その点に掛かっている応力の全てをひとまとめに表すことができる形式というか,断面を指定すれば自動的に応力が取り出せる関数のような便利なものはないだろうか？

そこで考え出されたのが応力テンソルという概念である.最小限の情報で,どんな向きの断面の力でもそこから導き出せてしまうという便利な形式になっている.

応力テンソルの定義

応力テンソルは次のような 9 つの成分を持った量である. それぞれの成分 $T_{ij}$ は,まっすぐ軸方向を向いた面を考えたときの軸方向に掛かる応力を表している.とを逆にして定義している教科書もあるが,後で分かるようにこの行列は対称になっていて $T_{ij}=T_{ji}$ という関係が成り立っているので,あまり気にしなくてもいい.ここではそのように定義して説明していこう.

これは物体全体の様子を表す量ではなく,物体内のどこか一点での応力を表す量である.物体全体をひねったりするような,ちょっと複雑な力の掛け方をしたときには,応力テンソルの各成分はそれぞれの場所でそれぞれ異なった値を持つ.

たくさんの成分があるからこれだけで物体全体を表せてしまうのかと期待してしまいたくなるんだよね.残念でした！

例えば $T_{xx}$ というのは,方向を向いた面に対して方向に掛かる応力なので,これは法線応力である.法線応力には圧力と引っ張り応力の二通りがあるのだが,引っ張り応力の場合を正の値で表し,圧力の場合を負の値で表すという習慣になっている.

土質力学・地盤工学では逆に定義されており,圧力の方を正にするという習慣である.引っ張り応力がほとんどない粒から成っている土を扱うので,そうしないと負の値ばかりになってしまうからである.それに合わせて剪断応力についても逆向きに定義されているようである.

分かりやすいように土質力学ではなく土木工学と書こうと思ったが,土木工学には構造力学や水理学も含まれており,それらでの定義は逆になっていないので,やはり土質力学と書くしかなかった.

流体力学も圧力が主役であって,引っ張り応力は出てこないのではないかと思うかもしれないが,この定義の違いで何が変わってくるのかを知れば納得が行くかもしれない.それについては後で説明しよう.

$T_{yy}$ や $T_{zz}$ も同様に法線応力である.つまり,この行列の対角成分が法線応力を表しており,非対角成分が接線応力を表していることになる.

なぜこれで最小限だと言えるのか

応力テンソルの成分は 9 つもあるが,本当にそんなに多数の成分が必要なのだろうか？逆の不安もある.本当に 9 つの成分だけであらゆる状況を表せるのだろうか？

それらの疑問に答えるためには次のようなことを考えるといい.まず,物質の内部に次のような四面体の領域を想像してみる.

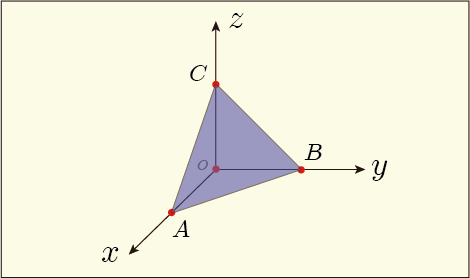
これら 4 つの面のうちの 3 つの面は法線が軸方向を向いているので,それらに働く応力は $T_{ij}$ を使って表せるだろう.残り 1 つの面に働く応力の表し方は分からないが,それらの組み合わせによって表せるのではないだろうか？

応力というのは物体を構成している粒子を運動させるような一方的な力ではなく,動かないようにその場で踏ん張ろうと耐えていることによって生じている力なので,全体の力が釣り合っているはずである.そのことを利用するのである.

図の 3 つの点,A,B,C の座標をそれぞれとすると,面 ABC の法線ベクトルは ( 1/a , 1/b , 1/c ) である.分母が 0 になる場合が気になるかもしれないが,,,のいずれか一つでも 0 になると図のような四面体は形成されないので,そのような状況は除外しておくことにする.また,それぞれの面の面積は次のようになるであろう. 上から順に,それぞれ軸,軸,軸方向を向いた面の面積だという意味である.最後の S_n は斜めを向いた面 ABC の面積である.この面積の公式が高校の数学の教科書に載っていたような覚えがあるが,現実の場面で役に立つことがあるとは思わなかった.

とりあえず,軸方向の力の釣り合いだけを考えてみよう.応力は面積あたりの力だったから,面積と掛け合わせることで力になる.面 ABC に掛かる応力の成分を $T_{nx}$ と表すことにすると次のような関係が成り立つ. 次のように書き換えよう. 試しにこの右辺の第 1 項にある面積比を計算してやると次のようになる. ここで,面 ABC の法線ベクトルが ( 1/a , 1/b , 1/c ) であったことを思い出して (n_x, n_y, n_z) という記号で置き換えればもう少しすっきりするのではないだろうか.しかしは単位ベクトルだという設定にしたいので,後でベクトルの長さを調整するために係数を入れて,次のような関係になっていることにしよう. すると先ほどの式は次のようになる. 調整のためのがあってもなくても関係ないというわけだ.とにかくは単位ベクトルだということで導入したので ${n_x}^2 +{n_y}^2 +{n_z}^2 =1$ という関係がなりたっており,この式はとても簡単になる. (2) 式の右辺の第 2 項,第 3 項についても同じような計算が出来て,結局 (2) 式は次のようになる. 軸や軸についての釣り合いも同じことで,次のような関係が成り立つ. 行列の掛け算のルールを使えば,次のように分かりやすい形でまとめられる. このように,知りたい面の単位法線ベクトルと応力テンソルがあれば,面がどんな方向を向いていたとしても,そこに働く応力を表すことができてしまうのだ！

これで最初の疑問が解決した.9 つの成分があればあらゆる状況を再現するための情報として十分であることが分かった.そして,これを計算するためには 9 つの成分がどれも使われている.つまり,9 つの成分がどれも必要なのである.

ところで,この力の釣り合いの関係で使っている $T_{ij}$ は同一の点での応力テンソルどうしの関係にはなっていないのではないかと気付いた人もいるだろう.正しいツッコミである.この話は四面体をどんどん小さくしていっても同じように成り立つ.だから無限に小さくしていった先で,ようやく同一点での応力テンソルの関係として正しく機能することになる.

むしろ大きな四面体を考えたときにはこの関係は正しくない可能性がある.この四面体の中に含まれる物質に体積力と呼ばれる重力などの外力が直接に掛かって,それを含めた形で釣り合いが取れている場合が考慮されていないからである.考える四面体を小さくすればするほどそのような影響を気にしなくても良くなるわけである.

断面のうらおもて

先ほどもちらっと話したが,地点における応力というのは,地点にある粒子を直接的に加速する力を表しているわけではない.応力というのは物体全体を押さえ付けたり引っ張ったりする外力に対してできるだけ動かないように物質が踏ん張ることで物体内部に生じている力である.

物体が動かないのなら,力が釣り合っているのだろう.その地点にある物体の粒子に掛かっている合力は 0 である.では応力テンソルは何を表しているのか？その地点に掛かっている力ではなかったのか？

この状況を矛盾なく把握するためには次のように考えてみてほしい.指定した断面の表には確かに力が掛かっている.しかしそのすぐ裏面には全く逆向きの力が掛かっている.そんなイメージである.そこにある物質は両方の力を受けるわけで,完全に打ち消し合って釣り合っているのである.

本当はつぶつぶの原子が集まって出来ている物体を,あたかも継ぎ目のない連続体として扱っているので,「厚みのない断面の裏と表に互いに逆向きの力が掛かっている」という不思議な表現になるのだが,そういう考え方をすることによって多数の原子の存在を無視して議論できるので楽なのである.

応力というのはそんな感じに働いているものなので,ある領域を考えたとき,その内部では互いに力が打ち消し合っていることになる.するとどうなるかというと,力を打ち消す相手のいない表面だけで力が働くのである.

我々が物体に圧力を掛けたり引っ張ったりねじったりするときのことを想像してみてほしい.必ず物体の表面を通して力を加えているではないか！

とは言っても例外がある.物体の内部に直接に体積力が働くとき,それは例えば重力のことであるのだが,物体の密度分布が一様でない物体を両手で支え持てば,内部をひねるような応力が勝手に生まれるだろう.今は説明のためにそういう体積力の存在を無視して話している.こういう場合分けをしないと正しい議論にならないので,ああ,面倒くさい.
今,場合分けと言ったけれども,体積力が働く場合については読者の方で勝手に考えてみてくれないだろうか？是非そうしてくれ！

しかし,力が掛かるのは物体の表面だけだと考えなくてもいい.流体力学などが特にそうだ.物体内に何らかの領域を勝手に想像してみる.多数の領域が,面を接して存在しているというイメージだ.これらの領域どうしは,互いの面を通して力をやり取りしているというイメージが成り立つ.

そういうわけで,応力を考えるときには必ず領域というものが重要になってくる.先ほどの議論でも四面体領域を考えてその表面に掛かる力を議論したのだった.本当はその計算を始める前にこういう議論が必要だったのだが,いきなりこんな話から始められても嫌になるだろうから軽くごまかしたのである.

先ほど,断面には表と裏があるという話をしたのだった.今の話を踏まえると,考えている領域の境界面こそが重要であり,表か裏かという区別は,領域の外側の面か,内側の面かということで区別すればいいことになる.

圧力を負の値で表すというのは,領域の外側の面を表だと考えたときのイメージである.圧力は領域を内側へと押す力なので,負の値としてとらえるのである.このような定義を採用している分野では,断面の向きを表す法線ベクトルを領域の外側に向いているものと考えていることになる.

一方,圧力を正の値として扱う学問分野では,領域の内側の面を表として扱っているはずなので注意してみてほしい.

先ほどの計算でも法線ベクトルを四面体の外側に向けて考えていたし,各面に働く力についても実はそうしていたのである.(1) 式を立てるときに,そこを考慮して各項の正負を決めなければならないが,面倒な議論を避けて雰囲気で押し通したというわけである.

罪滅ぼしのために,今ここでやってみようか.「軸の正の方を向いた面」というのは四面体の内側を向いているので,裏面を指定していることになってしまう.例えば $T_{xx}$ というのは表の面に掛かる応力を表しているのだったから,符号を逆にして考えるべきである.他の 2 つの面も同様である.つまり (1) 式はまず,次のように立てるべきであった. 符号もしっかり考慮した上で,合力は 0 になる,という表現である.このように,隙のない議論をしようとするのはなかなか面倒である.とにかく,これで先ほどの議論は結果的に正しいということが分かった.

流体力学ではどうなのか

さて,応力というものは領域を想定したときにその表面でだけ意味を持つ,というまとめ方をした.

しかし,領域どうしは互いに押し合い,引き合いをしていて力が釣り合っているからこそ,動かないわけである.どの領域の境界でも力が釣り合っているのであれば,結局は物体の内部には物体を加速するような力は存在していないのではないだろうか？

固体の場合はそうである.実際,物体の内部は動いたりしない.しかし流体の場合はどうだろうか？各部が割と勝手にあちこちへと動く.じっとその場に耐えていないからといって応力が消えてしまっているわけでもない.

流体内部の応力の釣り合いはどうなっているだろうか？応力が釣り合っていないような面があるとは考えにくい.あるとすれば,その面を境にして応力が不連続になっているということである.そういうところがあれば境界面が動くだろう.実際に流体は動く.ああ,考えにくいな.止まっていてくれ.するとやっぱり応力が釣り合っていないような特別な面があるのか？そんな不連続な振る舞いをするとも考えられない.

応力がどこもかしこも釣り合っているのであれば,物体を少しも加速しないわけだから,流体力学では何の働きもしないのではないだろうか？体積力のような外力が働いていれば,それを取り入れた形で釣り合うようになるだろうから,離れた地点でそれぞれ応力が異なるということも起きるだろうが,外力がなければどうだろうか？応力が流体の加速を生み出すようなものでないとしたら,それを流体力学の理論に取り込む意味はあっただろうか？

……とまぁ,そんな感じのことを悩んだりしたのだが,すでに疑問点をかなり整理して書いているので,ちょっとわざとらしい表現になってしまっている.

結論を言えば,流体内部では応力は連続で,各点では力が釣り合っているが,場所ごとに滑らかに変化しているのである.応力の座標微分が 0 ではないのだ.ある程度の距離を考えたときには応力に差がでてきて,それが領域を駆動するというイメージになっている.

前回導いた方程式でも応力テンソルの座標微分という形で理論に入っているのが分かる.

……とまぁ,ここまで考えてホッと一息ついたのだが,すぐにまた疑問にぶつかった.固体であっても場所によって応力が違っていることがあるだろうし,それが連続的に滑らかに変化しているのは同じではないだろうか？そういう場合,流体は動いてしまえばいいが,固体は動かないで安定している.一体どういう理屈で固体内の物質は定位置で安定しているのだろうか？

少し考えて解決した.正体は弾性力である.弾性体と呼ばれるような物体は,元々の形からの変形を受けるとずれに応じた復元力が働いて,元の形を保とうとする.これは流体にはない性質だ.それ故に流体は流体なのである.地点による応力の差と,変形によって生じた弾性力がちょうど釣り合っていて,静止するという理解でいいだろう.

著者のぼやき：状況 A においては B が成り立つ.しかしそれとは少し違う状況 A' においては少し拡張した形の B' が成り立つと考えねばならない.ところがそこまで考えてみると状況 A においても B' が成り立つこともないわけではない.……という感じの話が今回はあちこちで発生した.こういう場合,普通の教科書としては「一般に B' が成り立つ」の一言で済ませるのだろう.

対称である理由

応力は領域の表面に原因があり,物体全体の表面にまでたどれるのだった.体積力が働くときには少し違ってくるが,それについては後で修正しよう.

物体の内部に応力をかけようとして物体を手に持つ時,物体全体が回転してしまわないように持つだろう.このとき物体全体にかける力のモーメントは 0 である.物体の外側をしっかり固定して持っているのに物体の内部が勝手に回り始めるということは起きない.

いや,ひょっとしたらそういうことが起きるかもしれない.物体の内部がいくつかの領域に分かれてそれぞれ逆回転を始めて,どんどん回転が加速して行ったとしても全体の力のモーメントは 0 だからだ.しかしそんなことがあるだろうか？物体の外側をちょっとひねっただけで物体の内部がどんどん回転して加速していく現象があればとても面白いのだが,残念ながらエネルギー保存に反するであろう.

このように考えていくと,応力というのは物体内部に力のモーメントを生じないと結論せざるを得ない.

このことを使って,応力テンソルの性質をもう一つ導こう.説明のために,物体内部のどこか一点を原点として定め,その付近に,,の微小な直方体を考える.

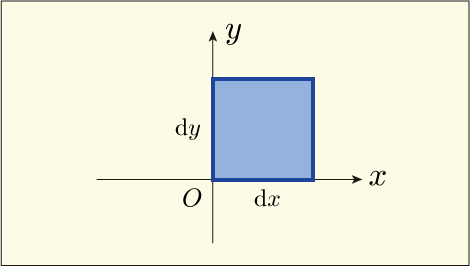
この図ではが描かれていないが,軸方向から見下ろしているところだと考えて欲しい.

このような微小領域の境界には様々な応力が働いているだろうが,その中で,この領域を軸の周りに回転させそうなものに注目してみよう.法線応力は真っ先に除外される.なぜなら直方体の反対側の面からも同じ大きさの応力が掛かっていて,打ち消し合ってしまうからである.

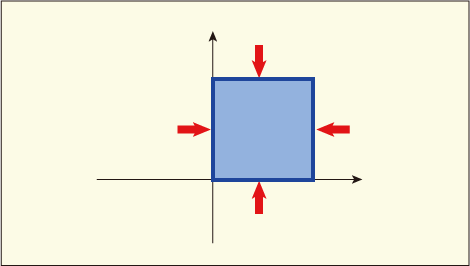
ごく僅かな差があるかもしれないが,考える微小領域を小さくすればするほど無視できてしまう程度である.どちらにしても回転には関係ない.

接線応力は同じようには打ち消されない.しかし打ち消すかどうかはあまり関係ない.原点を含む面に掛かる接線応力は原点の周りに回転させるようなものではない.

残るは $T_{xy}$ と $T_{yx}$ である.

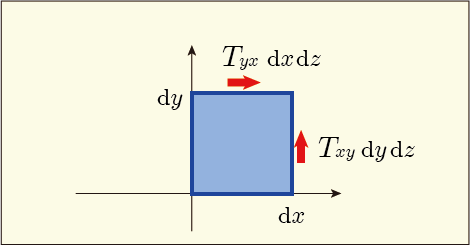
$T_{xy}$ は軸の正の方向を向いた面に軸方向に掛かる応力である.この面の面積は dy dz だから,力は $T_{xy} dy dz$ であり,これが原点から半径だけ離れた点に掛かっている.反時計回りに $T_{xy} dy dz× dx$ のモーメントを持つ.

もう一つの $T_{yx}$ は軸の正の方向を向いた面に軸方向に掛かる応力である.この面の面積は dx dz だから,力は $T_{yx} dx dz$ であり,これが原点から半径だけ離れた点に掛かっている.時計回りに $T_{yx} dx dz× dy$ のモーメントを持つ.

先ほどの話から,物体内部では力のモーメントは生じないはずであり,次の関係が成り立っていなければならない. つまり, $T_{xy} = T_{yx}$ である.

今は軸の周りで考えたが,他の軸についても同様に考えれば, $T_{yz}=T_{zy}$ や $T_{zx}=T_{xz}$ も言えるだろう.微小な直方体をどんどん小さくしていけば,これらの関係は同一地点での応力成分どうしで成り立つものだと言っていい.応力テンソルは 9 成分を持っているが,行と列の入れ替えに対して対称になっており,独立な成分は 6 つしかないということになる.

……と言いたいところだが,実はここまでの話には少し修正すべき点がある.体積力を全く考慮していなかったのだった.それについて考えてみよう.

例えば密度分布のせいで不均一の重力がかかる時はどうだろうか？物体は最も安定な姿勢へと傾こうとするだろうが,それを支える手が逆向きのモーメントを与えるので,物体は全体として静止した状態で安定する.物体内部が勝手に回転を始めてどんどん加速するような事は無いであろう.結論は変わりそうにない.

微小な直方体をどんどん小さくしていけば領域内の密度の不均一は考えなくても良くなってくるだろうし,小さくなればなるほど,長さの 3 乗で小さくなる体積力と,長さの 2 乗で小さくなる応力との比は大きくなって,体積力は無視できるようになるという論法を使ってもいい.

ただし,ここまでの考察が成り立たない場合もある.例えば,外部から強力な磁場を掛けることによって物体内部に分子レベルで大きなモーメントを加えた場合である.そういうことが起きている間は応力テンソルが対称であるという仮定が使えなくなる.しかし普通の現象を扱っている限りはそのようなことを心配する必要はない.

応力テンソルの座標変換

物体の中のある 1 点の応力を 6 つの要素で表すことが出来た.それだけでもう十分に満足してもいいのかもしれないが,もう少しだけ不満がある.

応力テンソルというのは軸,軸,軸を特別扱いしてはいないだろうか？

この座標軸は空間の中に人間が勝手に方向を定めて引いたものである.本当は別の方向を軸,軸,軸として定めて,それに従って別の数値の組み合わせで応力テンソルを作っても良かったはずである.

座標軸の方向を変えることで何通りでも異なる応力テンソルが作れたはずだが,それらどうしの関係はどうなっているだろうか？それが分かれば,特定の方向にだけ頼るようなことがなくなり,もっと広い視点を持つことができるだろう.

ある座標系を (x,y,z) で表し,それとは別の座標系を (x',y',z') と書いて区別しよう.話を複雑にしないために,両者の原点は一致しているとしておく.一つの座標系を回転させることでもう一つの座標系に重ねることができるので,これらは回転を表す 3 行 3 列の行列によって変換することが出来る. 回転行列が具体的にどんな形をしているかという話は面倒なのでここでは気にしないことにする.

大雑把に言えば,回転行列というのは直交行列と呼ばれるものの一種である.直交行列は二つのベクトルをそれぞれに変換した後でも互いの角度を保ったままだという性質がある.ベクトルの長さも変えない.つまり,3 つの座標軸を変換してもやはり直交したままなので,それが新しい座標軸として使えるのである.直交行列の行列式は ±1 である.直交行列には座標軸を鏡像反転させてしまうものも含まれているが,そのような行列の行列式は -1 なので,行列式が 1 になる方ばかりを集めれば,それが回転行列である.

さて,効率の悪い方法で良ければ,系で使える応力テンソルの各成分を求める作業はそれほど難しくはない.まず方向を向いた面に働く応力を導いてやる.そのためには軸が系の座標でどのように表せるかを求めてやる必要がある.(4) 式の逆変換を使ってやればいいだろう.その結果を (3) 式に代入してやれば面に働く 3 方向の応力が得られるだろう.しかしそれはまだ系の座標で表された成分なので,もう一度 (4) 式を使って系での表し方に翻訳してやる.こうして得られた 3 つの値を使っての 1 行目の成分が埋まることになる.同様にして面とについても計算してやれば完成である.

どの成分を得るにしても,2 回の座標変換を経ることが必要になる.

今のような計算内容をもう少し機械的に実現する方法はないだろうか？(3) 式は次のような形をしているのだった. 我々はこれと同じように系でも使える次のようなを知りたいのである. $(m_{x'},m_{y'},m_{z'})$ というのは系の座標で表された何らかの法線ベクトルである.

しかし今はたまたまとが同じ方向を向いたベクトルである場合について考えてみよう.その場合には両者の関係は次のように表される. 一方,(5) 式や (6) 式の左辺についても両者の関係が次のように表されるであろう. この (5) ～ (8) 式を組み合わせれば何とかなりそうだ.まず (8) 式の右辺に (5) 式を代入し,その結果として出てくるを (7) 式を使って書き換える.まずはそこまでやってみよう. この結果を (6) 式と見比べてやると,次のような関係になっていることが分かる. これが応力テンソルの座標変換を行うための公式である.座標変換の行列さえ分かっていれば,行列の計算ルールによって計算できてしまうのである.直行行列は逆行列 $R^{-1}$ と転置行列 ^tR が等しいという性質を持つので,次のように書いてもいい. わざわざの逆行列を求める必要もなくてとても助かる.

対角化

ところで,(9) 式のような形で実対称行列を変換したとき,直交行列をうまく選べばを必ず対角行列にすることができるという定理がある.応力テンソルは実対称行列であったからこの定理が当てはまる.これについて詳しく知りたければ線形代数を学んでみてほしい.「対角化」と呼ばれている話である.

対角行列というのは,対角成分以外は全て 0 であるような行列であり,次のような形である. これが何を意味するのかというと,法線応力しかないということである.たとえどんな複雑な応力が掛かっているように思えても,あたかも 3 軸方向からそれぞれ押されるか引かれるかという,そういう力しか掛かっていないと言えるような,そんな単純にとらえることのできる特別な方向が必ずあるということである.

このように対角化したときの 3 方向の法線応力,,のことを「主応力」と呼ぶ.そしてこのように見える座標軸を「主軸」あるいは「主応力軸」と呼ぶ.具体的な求め方を知りたければ線形代数を学んでみてほしい.

最初に 9 成分が全部必要だと言っていたくせに,実は独立な成分は 6 つだけであると言って,今度はとうとう 3 つの数値だけで状況を表せるという話になってしまった.どこまで騙すつもりだと思うかもしれないが,そういうわけではない.この 3 つの成分だけでは意味を成さないのである.これが意味を持つためには,どの方向を座標軸に取った場合にそれが言えるのかという情報も必要であり,それを指定するためにはやはり 3 つの数値情報が必要になるからである.

軸の向きを表すのに本当に 3 つの数値が必要であるかどうかが気になるかもしれない.例えば軸の方向を指定するために緯度と経度で 2 つの数値を使ったとして,他の軸が軸からどんな向きに伸びているかを指定するために角度の情報がもう 1 つ要るだろう.あるいは回転行列を使って軸の向きを表してもいい. の成分は全部で 9 つあるが,直交行列というのは 3 列を 3 つのベクトルだと見たときに,それぞれの長さが 1 で,互いに直交するという条件があり,このように計 6 つの条件式で縛られるので,独立な成分はやはり 3 つなのである.

流体力学に関係なさそうなところまで勢いで話したが,応力テンソルについてはだいたいこれくらいのことを知っていればおおよそ問題ないだろうと思う.もし他に必要なことが出てこればまたその時に追加で説明することにしよう.

エンドロール

今回の記事が予定外の大作になってしまったので,エンドロールを入れたくなってしまった.

制作協力 by マしつぶのひ様

この作業,全部一人でやってるんですけど！という思いが高まって,ネットでつぶやいたのがきっかけである.最初は原作も EMAN と書いていたのだが「物理の原作は神様じゃないですかw」というツッコミが入り,それもそうだな,と謙遜な気持ちになったところで有志の方が他の方々のツッコミも取り入れて即興で制作してくださった.宗教アニメや個人制作のクソゲー,あるいは80年代アニメっぽい感じが奇跡的にミックスされていてとても気に入っている.

応力	法線応力（垂直応力）	圧力（圧縮応力）
		引っ張り応力
	接線応力（ずれ応力）（ずり応力）（剪断応力）（せん断応力）