粘性の具体例
前回の記事で応力テンソルのイメージが分かってきたと思う.今回は流体の応力テンソルを具体的にどう表したらいいかという話である.そのためには粘性の話をしなくてはならない.
まずは具体的な例を見た方が分かりやすいだろう.2 枚のガラス板の間に油などの流体を挟んで,ガラス板を滑らせることを考えてみる.
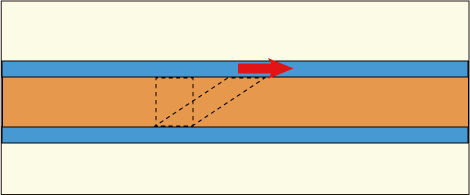
下側のガラスを固定して上側のガラスを動かしてやると,粘性のある流体というのは固体の表面に付着して一緒に動こうとするので,挟まれた流体はこの図のような変形を起こす.さて,書いておいてこう言うのも何だが,本当にそうだろうか?
粘性のある流体が固体の表面にへばり付いて相対速度を持たないというのは実験的な事実であるらしい.そうなる理由は理論的にはよく分かっていないようだが,そのように仮定してシミュレーションを行うと現実と良く合う結果になるそうだ.そういうわけで,上では「ガラス板」と書いたのだが,実はどんな材質の板であろうと同じ結果になるので気にしなくてもいい.
材質を気にしなくていいというのは流体力学にとって大変にありがたい話だ.材質によって話が変わったのでは面倒くさくてかなわない.今後は形状に集中すればいいのである.
では本当にこのようにきれいな平行四辺形を保って変形していくのかというと,これはまぁ,理想論である.動かす速さが速すぎると流体内に乱流が生じるのでこのようにはならないだろう.また,流体の層が厚すぎれば力が伝わるのに時間がかかるので流体の変形に遅れが生じるだろう.そういうわけで,このような理想的な流れには「クエット流れ」あるいは「単純剪断流れ」という名前がわざわざ付けられている.クエットは人名である.
クエット流れというのは,流れが平行に揃っていて,流れに対して垂直に視点を移動すると,その距離に比例して速度が変化しているような流れ方のことである.
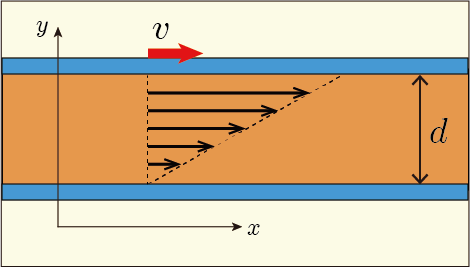
理想論とは言ったが,このあとで説明するような特殊な流体を使わずに,力が全体に到達して安定するくらいに十分に長い時間ずっと一定速度を保ちながらごくゆっくり板を移動させれば,このような流れ方が実現することが理論的にも導かれる.しかし今は粘性の話を急ぎたいのだから,そういう理論の話はまたいつかしよう.
このような実験をした時に,板を一定速度に保つためには力を加え続けることが必要である.それは板の移動速度
,板の面積
に比例しており,流体の厚み
に反比例することが知られている.
は流体の種類によって決まる定数であり,粘り気の強さを表しているようである.雰囲気的にいかにも成り立ちそうな関係であろう.この比例定数
を「粘度」あるいは「粘性係数」と呼ぶ.
この「粘度」を密度で割った「動粘度」という概念もあるのだが,話をややこしくするだけなのでここでは触れない.動粘度と区別するために「粘度」のことを「絶対粘度」と呼んだりもする.
加速もしないで一定速度で動かし続けるためだけに力が要るのだから,エネルギーが次々と失われて熱に変わっているのだろう.つまり粘性というのは流体の中で働く摩擦力のようなものだと考えられる.
ニュートン流体
この (1) 式の関係が成り立つ理由をもう少し細かい視点で眺めてみよう.ある断面に対して平行に,面積あたりに働く力を接線応力と呼ぶのであった.この移動させている板と流体の間にはという接線応力が働いていると言えるだろう.接線応力を
という記号で表すと次のように書き直せる.
さらに,この式の
の意味を考えてみる.
は板の移動速度だが,流体の一番上の層も同じ速度で動いているのだった.クエット流れが実現している場合,流体の最下層からの距離に比例して流速が決まっているのだから,
というのはその変化の割合を意味していると考えられる.すると,ひょっとすると,各点での速度変化の割合によって各点での接線応力が決まるという法則が成り立っているのではないだろうか.板の速度
ではなく,流速
を使って式で表すと次のようである.
この関係式を「ニュートンの粘性法則」と呼ぶ.
この法則は天然に存在するほとんどの流体では成り立っており,この法則が成り立つ流体のことを「ニュートン流体」と呼ぶ.しかし近代になって合成されるようになってきた高分子溶液やコロイド溶液などでは成り立たないことが多く,この法則が成り立たない流体のことを「非ニュートン流体」と呼ぶ.
流体力学にまでニュートンの名前が出てくるのはなぜだろうと奇妙に思ったのだが,ニュートンも流体現象について研究していたようなのである.かの有名なプリンキピア全3巻の第2巻では流体について論じてデカルトの渦動宇宙論を批判している.ここまでに既にオイラーやラグランジュの名前も出てきているように,ニュートン力学はかなり早い段階で流体の運動の考察にも取り入れられている.このように流体力学の歴史はかなり古いのである.
(2) 式の右辺に出てくるのことを「速度勾配」「ずり速度」「剪断速度」と呼んだりする.
非ニュートン流体
非ニュートン流体では (2) 式が成り立たないということだが,だとすれば代わりにどんな性質を持つのかと思うかもしれない.話は簡単で,(2) 式で使われている粘性係数が定数ではないと考えればいいのである.面倒くさい式を考えなくても,(2) 式からずれる理由を,すべて
が変化するせいにしてなすりつけてしまえばいい.
非ニュートン流体にも幾つかの種類があって,次のようなグラフで表せば分かりやすいだろう.
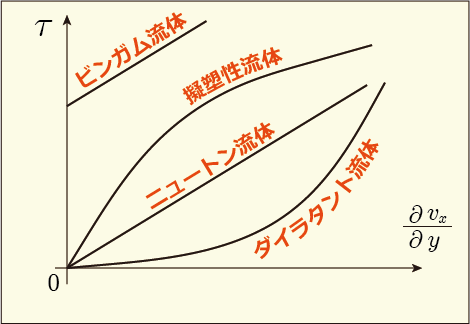
横軸が速度勾配であり,縦軸がその時に生じる接線応力である.ニュートン流体はが一定だから直線として表されている.
「ダイラタント流体」というのは,速度変化が激しいと急に粘性を増して固くなる流体である.小麦やデンプンなどの高分子の物質を大量に溶かした水の上を歩くパフォーマンスを見たことがあるかもしれない.その上でじっとしているとただの水のように振る舞うので沈んでしまうのだが,急いで歩けばまるで固い地面の上のように歩ける.このような性質,現象は「ダイラタンシー」と呼ばれている.
「擬塑性流体」というのはそれとは逆で,ゆっくりしているとドロッとしているが,速くかき混ぜるとサラサラになるような性質を持った流体である.マヨネーズやケチャップなどが身近な例としてよく挙げられる.いずれも高分子である.ボールペンのインクなどもそのような性質を追求して作られていたりする.
「ビンガム流体」というのは擬塑性流体に似ているが,静止しているときから剪断応力を持つものである.身近な例としてはマーガリンや歯磨き粉などが挙げられる.静止している限りは形状を保つが,素早くかき混ぜている間は流体のように振る舞う.流体の定義は静止時に剪断応力を持たないことだったから,厳密には流体の定義から外れるだろう.
非ニュートン流体は扱わない
こうして見ると非ニュートン流体の特殊さがよく分かるだろう.ほとんどの流体力学の教科書では「本書では非ニュートン流体は扱わない」と宣言している.ニュートン流体に限っても書くことが十分に多いからである.私も今後はニュートン流体に限って話すことにしよう.
非ニュートン流体が特殊であることを強調しようとして,逆にニュートン流体では粘性係数 が常に一定であると思い込ませてしまったかもしれない.しかし
は温度や圧力によっても変化するものであることを忘れてはいけない.とは言っても大抵は
を定数として扱っても問題ないだろう.
普通に流体力学と言えばもう「ニュートン流体」の話をしていると思ってもらっていいくらいである.そもそも粘性がない流体(完全流体)の話だけで教科書のかなりのページを占めていて,粘性流体が出てくるのは後の方だったりする.非ニュートン流体について詳しく論じている余裕は無いのである.
さきほどクエット流れの話をしたときに「特殊な流体を使わずに板をゆっくり一定速度で動かせばクエット流れが実現することが理論的に導かれる」と書いたが,あれは「ニュートン流体を仮定した場合には」そうなるということである.クエット流れはイメージを描きやすいように例として使わせてもらっただけであり,(2) 式のニュートンの粘性法則はクエット流れが実現していない場所でも成り立つと考えて使ってもいい.
色々話したので一旦ここで話を切ろうか.応力テンソルを具体的に表すところまで行けなくて申し訳ない.










