物理数学：不偏分散の疑問

期待値の性質

前回の記事の数学的な補足である.不偏分散を計算するときに n-1 で割るのはなぜなのかという話である.

大抵の統計の入門書では軽く誤魔化しているので「なぜなのか」とすごく気になってしまう人も多いのではないかと思っていたが,前回の話を読んでしまうと,「ああ,数学的に多分そうなんだろうな」と思えてきて,もうあまり気にならなくなっていたりは・・・しないかな？

本題に入る前に少しだけ準備をしておきたい.前回は期待値というものを母集団の平均値という意味だけで紹介したのだった.今回はこの計算を数学的な道具として積極的に使ってみたいので次のように表現してみる. これは変数が出現率 f(x) に従って確率的に得られるときの期待値を意味している.もし E[y] というのが出てきて,の値の出現率の分布が g(y) である場合には次のような意味になるものだとする. もし E[x+y] というものが出てきたとすると,これは出現率 f(x) であるところからたまたま引いたという値と,出現率 g(y) であるところからたまたま引いたという値の和を作る作業を何度も何度も行い,それら全ての平均値を意味するようにしたい.これを計算するには, $x=x_{0}$ かつ $y=y_{0}$ という値を拾う確率密度が $f(x_{0})g(y_{0})$ であることを使ってやればいい. 結果だけ見ると,なんとまぁ単純な関係である.変形の途中で,それぞれ単独の確率密度だけで全範囲を積分すると 1 になることを使っている.さらに定数,などを入れて拡張してやろう.同様の計算をしてやることで,次のような関係が成り立っていることも言えるだろう. こんなにきれいな関係が成り立っているのを見ると, E[xy] というものがどうなるかというのも気になってくる.実はこれも同じような考えで簡単に計算ができる. 非常に分かりやすい関係だ.さらに考えると定数を使って次のような関係も言える. これは毎回確実にという定数値が出る場合の期待値だということで受け入れよう.

さて,母分散というのは次のような定義であった. 前回と少し違っているのは母分布の期待値をではなくで表すことにしたからである.今回は E[x] を多用するので区別しやすくしておいた.この式は次のように表現することも出来るだろう. ところがこの式の右辺を先ほどの性質を使ってバラそうとするとおかしなことが起こる. この変形はやってはいけないのだ.上で説明した性質はととがそれぞれ独立に得られるものだという前提を使っている.ところが今回はの値を得て 2 乗した.同じ値どうしを掛け合わせたことになる.つまり,独立に得た二つの値を使っているという条件が満たされていないのである.

この辺りのことを気をつけながら,今回の本題に入っていくことにしよう.

なぜ不偏分散は n-1 で割るのか

知りたいのは「なぜ不偏分散は n-1 で割るのか」ということだった.不偏分散は次のように定義されていたのだった. は回の実験値の平均値である.これも混乱を防ぐために,前回とは記号を変えてある.

さて,疑問を言い換えれば,「なぜ n-1 で割るとうまくいくのか」ということであり,さらに言い換えれば,不偏分散の期待値 E[W] が母集団の分散に等しいのはなぜか,ということだ.式で表すと次のようになる. この式が成り立つことが示されれば,納得するしかない.では左辺の変形を進めよう. ここらで,カッコ内の二つの項を分けて説明しよう.まず最初の項は次のような変形が可能だ. 説明は要らない気がしてきた. x_i は測定値を意味しているが,母集団の期待値との差を使って期待値を計算しているのだから,それは母分散と同じ値になるのは当然だ.

次の項に含まれるは回の測定の平均値だという定義に書き戻して変形してやることにする. とてもややこしい感じがしてきたが,ここが今回の一番の山場で,考えるのが面白いところだ.ここでとのあらゆる組み合わせの和を考えている.このとは回の測定の中で何番目に取得したデータであるかという意味だ.先ほど分散の式をバラそうとしておかしなことが起こってしまった場面を思い出してみてほしい. i≠j ならば,番目に取得した測定値と番目に取得した測定値は独立しているから,先ほどのような変形をしてもいいのである.そして先ほども見たように,値は 0 になる. i=j となる場合だけは残さなくてはならない.それで,続きは次のようになる. さあ,これらを元の式に戻して結果を見よう. 予告通りである.めでたし,めでたし.

なぜ不偏分散をnで割ったものの期待値が平均値の分散になるのか

次に考える疑問を式で表してみよう.不偏分散を測定回数で割ったものは前回の記事ではと表していたのだった.もし回の測定を何度も何度も繰り返すと,そのたびに違った値のを得るだろう.その期待値は E[X] と表せる.それが平均値の分散に等しいというのである. 状況を式に表そうとしてとっさに V_m という記号を作ってしまったが,この意味をはっきりさせないといけない.平均値の分散とは何だっただろうか.回セットの測定を何度も何度も繰り返すたびに,個のデータを使って平均値を算出したものがであり,その値は毎回異なっている.その平均値ばかりを集めて作った平均値と,毎回の平均値との差を 2 乗して足し合わせて,全部の平均値の個数で割った値である.平均値の個数は有限ではなく,無限回行うのである.

これをどうやって式で表そうか.平均値ばかりを集めて作った平均値というのは,母集団の平均値に等しくなるだろう. E[m]=μ である.はガウス分布に従って出現する変数なのだった.ガウス分布に従って出現する値を使って (m-μ)^2 を計算して,その期待値を算出するのだから, と表せば良いだろう.上の方で V=E[(x-μ)^2] と表したのと同じ原理だ.ところがこの右辺は,先ほどの疑問を解決するための式変形の途中で既に出てきている.ちょっと探してみてほしい.「を定義に書き戻して変形してやることにする」と言っていた部分だ.次のような結論が出ているはずである. さらに先ほど解決した疑問は E[W]=V という式で表されていたから,右辺のを E[W] で置き換えよう.ここまでの変形を一気に書き並べると次のようになる. V_m が E[X] になることが示せてしまった.疑問はあっけなく解決だ.めでたし,めでたし.

なぜ X が平均値の分散に近い値だと信じていいのか

E[X] が平均値の分散 V_m に等しいということは導き出せた.しかし回きりの測定で得られるのは E[X] ではなく,である.このがなぜ V_m に近い値になっていると信じられるのかというのが最後の疑問だ.

回セットの測定ごとに得られるの値はどのような分布で出現するのだろうか.それが分かれば疑問は解決する.ある値の周辺でとても狭く尖った分布になっていれば,滅多なことでは大きくハズレた値は得られないはずで,信用ができると言えるだろう.

その辺りを探るヒントはないものかと探し回ってみたところ,やっとのことで使えそうなヒントが見付かった.「 $\color{red}{χ^2}$ (カイ2乗)分布」と呼ばれるものだ.これは統計学の教科書に必ずと言っていいほど出てくるものだが,今から調べようとしていることとは異なる目的で紹介されることが多いもので,その存在に気付くのが大変遅れてしまった.

これは標準正規分布に従って独立に個の変数 x_i を得てという値を計算したときの,このの分布がどうなっているかを意味するものであるらしい.標準正規分布というのは 0 のところにピークがあるような標準偏差が 1 のガウス分布のことである.これは大変に都合がいい.なぜなら,我々の今の目的からすると,回の測定を行ったときに,毎回母集団の期待値を引いてから 2 乗して和を取ることに相当するからで,ピークからの差の 2 乗和という意味になっている.これを n-1 で割れば不偏分散の意味になるし,さらにで割れば,今知りたいになるわけだ. ただ少し違うのは,我々はこれまで母集団の分布がガウス分布だとは仮定してこなかったし,標準偏差も 1 ではなかった.しかし,標準偏差の違いはグラフの横幅のスケールが変わるだけの話であるし,今の目的はの分布の様子がどうなっているかが大雑把に確認できればいいだけなので,母集団の分布がガウス分布だと仮定して話を進めることにしよう.

このカイ二乗分布の式を求めることはここではやらない.式を見てもらえば今はそこまで手を出さない方がいい理由が分かってもらえるだろう. ガンマ関数というちょっと特殊な関数まで使われているが,最初の分数の部分は全体を積分したときに 1 になるようにするための調整部分だからあまり気にすることもない.は負の値にはなりようがないので, z<0 の領域では h(z,n)=0 である.

が増えるほどが増えるのは当然なので,だんだんと横に広がっている. h(z,n) をで微分して 0 になるところを求めてみれば分かることだが,ピークの位置は n-2 であり,だんだん右へと向かっている.さあ,これを n-1 で割ることで不偏分散の分布のグラフに変えてしまおう.

n=1 の曲線は,0 での割り算になるので存在しない.これは分布のグラフなので全範囲で積分したときに 1 になるようにグラフの高さをそれぞれ変えるべきだが,線が重なって分かりにくくなるのでそれはやっていない.雰囲気を見てもらいたいだけなのだ.測定回数が増えるほどピークの横軸が 1 に近付く.これは元々標準偏差が 1,つまり分散も 1 であるような分布から抜き出してくるという設定なので当然だ.元々ピークが n-2 になるところを n-1 で割って縮めているので, (n-2)/(n-1) ,すなわち 1- 1/(n-1) となり,確かにそうなることが分かるだろう.

さて,我々は不偏分散をさらにで割ってを算出したのだった.次のグラフは横軸のスケールを 1/n に縮めたものである.つまり,それぞれの曲線ごとに縮め方を変えるのであり,が大きいほどギュッと縮めてある.左へ寄り過ぎるグラフになるので,原点近くの細かい挙動を観察しやすいように全体的に拡大してある.

これは偶然に頼っての値を一度だけ得るときの分布を表していると言えるだろう.確率分布を表すのなら各曲線が作る面積が 1 になるようにしておくべきだが,相変わらず各曲線の係数の調整はしていない.

本当に見たければ各自でやってみてくれ.

が大きいほどピークが左へ寄る傾向が見えてきている.当たり前といえば当たり前だが,この性質を見たかったので一安心だ.しかしグラフのピークから右側への分布がなだらかに長く続くところが気になる.これでは大き過ぎる値を引いてしまう可能性が高いことになるからだ. n=5 くらいになるとそれもあまり気にならないくらいにはなってくるけれども,一度気になってしまったものは気になって仕方がない.

しかし,我々が実際に誤差として併記するために使うのはなのであった.この平方根を考慮してグラフを書き直してやったら右側への坂道も引き締まるのではなかろうか.横軸が平均値の標準偏差になるように変更してやろう.

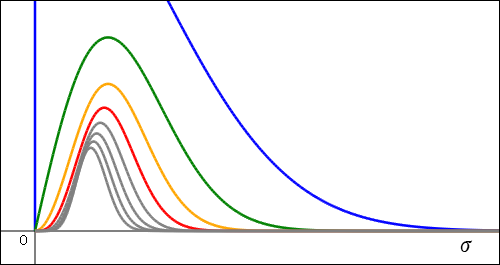
これは元々の横軸の 4 の辺りの確率密度を 2 の辺りに,9 の辺りの値を 3 に,16 の辺りを 4 に来るように書き直しただけである.つまり,ぐっと左に寄ってくることになる.左に詰まって見にくくなったので,またスケールを変更して原点付近を拡大してある.

この結果はなかなか良いのではないだろうか？左右対称に近い感じに引き締まってきた.今までは n=6 までの曲線しか描いてこなかったが,ここではさらに増やすとどうなるかを書き加えてある.が増えるほどグラフのピークが左へ寄っていっているのは標準偏差が実際に小さくなって行っているのであり,これは測定回数を増やすほど真の値を正確に推定することができるようになっていっていることを意味する.また,が増えるほど曲線の横幅がだんだんと狭くなっていっていることも分かるだろう.もしちゃんと全体の積分が 1 になるように調整すればが大きいほど上へ鋭く突き抜けた形に描かれるはずで,ここではやらないけれども,もしそれを見ればイメージも変わるはずだ.

我々が本当に欲しいのは,偶然に頼って得るではなく,それを無限に繰り返して得られる E[X] であり,もしできるなら σ=√(E[X]) として測定値の平均の値に併記したいのである.現実的には無理だから σ=√X を仕方なく使っているのである.このグラフでは曲線が左右対称ではないから多少は違うけれども,ピーク辺りがを意味していると思われる.そこで気になるのは,確かに曲線の横幅はが増えるほど減っていくけれども,それは √(E[X]) に比べてどうなのかということである.得たいと思っている値に比べてのばらつき具合はどう変化しているだろう？そこで,ピークの位置が揃うように曲線ごとの横幅の比率を変えてみよう.

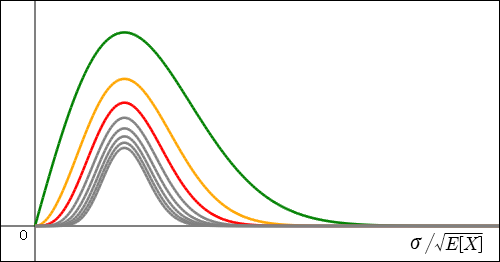
n=2 の曲線にはピークがないので消した.が大きいほど,実際よりも横に大きく引き伸ばしてあることになるのだが,それでも横幅が徐々に狭くなっていっているのが分かる.ピークの位置がおおよそ √(E[X]) だろうと考えられ,そこが本当にほしいの値だが,そこから何倍も外れた値が出てしまう可能性はとても小さくなっていっている. n=5 では多少心配だが, n=10 くらいならもっと安心できる.

記事を書く前はもっと鋭い形になることを期待していたのだが実際にやってみるとそうでもなかった.測定回数を増やしても急に幅が狭まるわけでもないし,これくらいの幅があることを覚悟して使うしかないのだろう.桁は合っている,と言えるくらいのものだ.平均値の標準偏差は測定回数に依存するようなものであり,物理的な対象に関する値ではない.測定の質を表すデータである.大体の目安を意味する数字であったのだからこれくらいでも仕方ないのだろう.