グラフ用紙を紹介
急激に増加する値をグラフに表す時に,普通のグラフで表そうとするとあっという間に表示範囲を飛び出してしまい,変化の全体の様子がよく分からなってしまう.それでは困るのでデータの全体が収まるように描こうとすると縦軸のひと目盛りをかなり大きな値にする必要があるだろう.そうなると値の小さなデータはほとんど横軸すれすれのところを這うことになってしまうから変化しているのかどうかがよく分からなくなってしまう.
そんな時には縦軸の目盛りを対数を使って表すことがよく行われる.分かりやすく言えば,縦軸の目盛りが値の桁数を表すようにするのである.縦軸を一定の長さだけ進むごとに値の桁が一つ上がるのである.このようなものを「対数グラフ」と呼ぶ.
もちろん値が急激に増加する場合だけでなく,急激に減少する場合にも使われる.
対数グラフを描くための用紙が売っている.

片対数グラフ用紙 (Amazon)
普通のグラフ用の方眼紙しか見たことのない人はこれを見てびっくりしてしまうかもしれない.商品になるほどに需要のあるものなのかと驚く人もいるだろう.私がそうだった.最近はコンピュータでデータ処理するのが当たり前になってきているから,このような用紙を使う機会は減っているかもしれない.コンピュータなら命令一つで対数グラフとして表してくれたりする.しかし機械に頼りすぎると見過ごしてしまうこともあるので,一度くらいは紙と鉛筆に頼った原始的な体験をしておくのもいいだろう.
パラパラとめくってみると,中は次のような感じの線が引かれた紙の束である.

クリックで全体を表示
印刷してじっくり眺めてみたい人のためにA4版のPDFファイルも用意しておいた.実物を手にすると画面越しに見るのとは印象が全く違っているから,使わないとしても一度そういう体験をしておくのも良いと思う.
さて,初めての人はどう使っていいか分からずに困惑させられるのではないかと思う.まず,「0 をどこにしたらいいのか?」「0 はどこだ?!」と騒ぎ始めるだろう.そんなものはない.もしあるとすれば下方向の無限の彼方だ.それはなぜかと言えば,例えばこの縦軸のどこかに 1 があるとしよう.そこから一定の長さだけ下に進むと 0.1 になり,さらに同じだけ下に進むと 0.01 になり,こんな具合にいつまでも 0 にはたどり着かないというわけだ.
では 1 はどこなのかというと,これもまた探しにくい.グラフ用紙の全体を眺めると何となく同じパターンが縦方向に繰り返していることが分かるだろう.そのたびに桁が一つ変わっているのである.その区切りはどこだろうか?
線の太さなどからその意図を見抜かないといけない.上に行くほど線の間隔がだんだんと狭くなっていくのだが,あるところでまた急に広くなる.間隔が広くなりすぎるとデータを書き込む際に位置を決めにくいので,親切心から間をさらに細い線を使って区切っているのだが,それもだんだんと密になっていくので,そのような親切は途中で打ち切らざるを得ない.打ち切ったところで急に幅が広くなっているように錯覚してしまうので,本当の桁の区切りが分かりにくい.慣れればすぐに判断できるが,最初はまごつくことだろう.
百聞は一見に如かずだ.先ほど見せた用紙の場合,例えば次のように値を振ることになる.
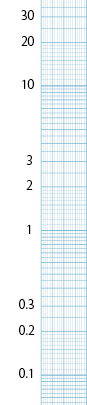
クリックで全体を表示
ここで 3 つくらいの疑問が一気に出てくる.
疑問1.縦方向の縮尺を変えることはできないのか?
このような用紙を使っている限りは無理である.普通の方眼紙の場合には縮尺を自由に設定して使うことができたが,このような用紙では制約を受けることになる.コンピュータを使ってグラフを描く場合には縮尺を変えることは可能であるし,ウェブ上で縮尺を設定して好みの印刷用PDFを作れるようなサイトもある.
・Logarithmic Graph Paper PDF Generator
・方眼紙ネット
とにかく,一度紙にこのような線を引いてしまうと,それに従う必要があるわけだ.
疑問2.1 がそんなところにあるなら,例えばデータの値が 10-8 とかの場合だと用紙の下の方すぎて書けないのでは?
心配は要らない.好きな桁だけ上下にずらしてデータをプロットすればいいのである.先ほどは説明のために 1 を用紙の中心辺りに書いただけであって,縦軸には自分が表したい辺りの桁を書き入れて使えばいい.
疑問3.横軸はどこに引けばいいのか?
多分これまで,縦軸の基準は 0 にしなければならないという原則を習ってきたのでそういう心配が出るのだと思う.対数グラフの場合には縦軸が 0 になる点が存在していないので,グラフが見やすいような位置に横軸を引くしか無い.
疑問4.その用紙だと 4 桁くらいの範囲しか表せないが,さらに広い範囲を表したい場合はどうするのか?
ほとんどの場合そういうことは必要ないが,もし必要ならもっと密に引かれた用紙を探してきて使うか,糊でつなげて範囲を拡大するしかないだろう.
何が読み取れるか
実験や観測で得た値をこのようなグラフ上にプロットしていき,もしそれがぴったり直線上に乗れば,それは
という指数関数的な関係になっていることになる.なぜそんなことが言えるのかを説明しよう.生の観測データが
だとすると,今はグラフ用紙上の実際の位置
を
という変換を使って表示していることになる.
というのは対数目盛を作るときの縮尺であって,特に意識して決めているわけでもない何らかの値である.グラフ上の直線というのはこの
を使った
という式で表されることになるだろう.この (3) 式に (2) 式を代入して変形してやると
となって,
と
の関係が (1) 式のようになっていることが分かる.ただし,この途中で
のような置き換えをした.
この計算過程を見ると,まずグラフ上で定規などを頼りにして (3) 式で表されるような傾きと切片
を求めてから,(4) (5) 式の関係を使った計算によって (1) 式の
や
に変換する必要があるように思える.しかしそれは手間が多いし,不正確な要素が入り込む可能性が高く,賢い方法ではない.
そんなことをせずとも,というのは (1) 式で
としたときの
の値であるから,グラフの
となっているところの縦軸の方に書いてある値をそのまま使えばいいだろう.
ではの方はどうやって求めたらいいだろうか?グラフに引かれた直線上の異なる 2 点の読みがそれぞれ
と
だったとしよう.ただし
とする.直線の傾き
は次のように表せるだろう.
この式を底の変換公式で変形すれば次のようになる.
この
を
に変換するにはどうしたらいいだろうか?(5) 式の両辺の対数を計算すれば,
であるから,
に
を掛けてやれば
になることが分かる.つまり,次のような式が成り立つことになる.
この計算をするのに定規は要らない.対数目盛の縮尺
も関係してこなくなる.
このように,グラフの縦軸は常用対数で目盛りを振ってあるのだが,(1) 式のような指数関数の形でどう表せるかが簡単に調べられるのである.
測定値というのは誤差を含んで値がばらつくものであるから,きれいに直線の上に並ばないかもしれないが,なるべく多くのデータが乗るような直線を引いてやり,その直線上の 2 点を (6) 式に当てはめて計算してやることでの値が決定できることになる.その際,2 点はなるべく直線上の両端に近いところから選んだ方が正確になるだろうし,数値が読みやすい点を選んだ方が良いだろう.
「なるべく多くのデータが乗るような直線」と書いたが,多数決で決めていいものではないので,「その直線から大きく外れるようなデータがなるべく少なくなるような直線」だとか,「その直線の上下にデータが均等にばらつくような直線」だとかいう表現をしたほうがいいかもしれない.要するに最小二乗法のようなセンスが必要になるわけだが,それについてはいつか別の記事で説明することにしよう.
世の中には指数関数で表されるような現象が数多いが,さまざまな要因からそこからずれる場合もあって,必ずしも対数グラフ上で直線になるとは限らない.無理に直線で近似するのが適当でない場合もある.対数グラフ上であっても傾きがどんどん増加していくような場合,指数関数よりも素早く増加するような関数,例えば階乗のような関数に従っている可能性もある.
使い方は工夫次第
大抵の場合は縦軸を対数目盛にするのだが,時には横軸の方を対数目盛にしたいこともあるだろう.そういうときは用紙を右に 90°回転させて使えばいい.
また,負の値を扱いたいときは用紙を 180°回転させて使えばいい.まぁ別に回転させなくても,縦軸はを意味すると断って上を負の方向として表示してもいい.そういうグラフもよく見かける.
とにかく,グラフ用紙によってグラフの形式が制限されるということは起こらないのであり,そういう使い方もあるのだということを思い出して欲しい.しかし,あらかじめ数字が印刷されてしまっているような用紙というのもあって,その場合には使い方が限られてしまうだろう.
両対数は次回
今回は縦軸だけが対数目盛になっている場合の話をしたが,縦軸も横軸も対数目盛になっているようなグラフを使うことがある.そのようなグラフを「両対数グラフ」と呼ぶ.両対数グラフの話は次回にしよう.
今回の話に出てきたようなグラフは両対数グラフと区別するために「片対数(かたたいすう)グラフ」という呼び方をすることもある.











驚かれたりする。