ゲルマン行列以外を採用する可能性
前回は生成子どうしの間に成り立つことを課した直交規格化条件の意味について説明したのだった.
この条件を満たしてさえいれば構造定数が反対称性を持つことが言えるのだから,この後の議論で特にゲルマン行列だけを使う必然性というものが少し揺らいできてしまった.ゲルマン行列というのは,8 次元空間の中で正規直交基底を選ぶのと同じくらい連続的で無限にある組み合わせの中の一つであるということになる.
ゲルマン行列以外にはどんな組み合わせが使える可能性があるだろうか?例えば何らかのユニタリ行列を用意して 8 つのゲルマン行列のそれぞれに次のように同じ変換をほどこしてやる.
対角和のカッコの中では最後尾の行列を最前列に移動させても値が変わらないので,このように変換して作った
どうしの間には次のような関係が成り立つことが言えるだろう.
要するに,ゲルマン行列に (2) 式の相似変換を施して作った生成子であっても同じ性質を持つというわけだ.
そこで次の疑問がやって来る.(1) 式を満たすような生成子の選び方は,(2) 式による変換によって表現し尽くされているだろうか?
答えは NO である.他のバリエーションが存在している.しかしそれを説明するためにはもう少し視野を広げておく必要がある.
対角行列は入れておきたい
ゲルマン行列のうちの二つは対角行列になっていた.(2) 式による変換を行うとそれらが対角行列ではなくなってしまうことの方が多いし,生成子の中に対角行列を含むことは必ずしも必要ではない事がわかる.しかし対角行列を選んでおくと状況が簡単に把握できて楽なのである.
そういう意味でゲルマン行列というのは無数の可能性の中からかなり特別な選び方がされているものだと言えるだろう.
しかし,対角行列を含むように選んだことだけがゲルマン行列の特別さだというわけでもない.対角行列の選び方はゲルマン行列が採用しているものの他にもあり得るのではないだろうか?そのあたりを考えてみたい.
SU(N) の生成子は次の行列であるから,対角成分は
個ある.ユニタリ行列の行列式が 1 であるという条件は生成子の対角和が 0 であるという条件によって満たされるので,対角成分の値は 1 自由度分だけ縛られる.
ここをもっと正確に言えば,ユニタリ行列の行列式が 1 である条件は生成子の対角和が(
は整数) という条件と等価だと言えるわけだが,普通は
を選んで縛りを入れるわけである.
よって対角成分には個分の自由度があることになる.SU(3) の場合には 2 個分の自由度があって,これを利用して最大 2 個の対角行列を互いに独立な生成子として選んでやることが出来るのである.このとき,対角行列以外の生成子の対角成分は全て 0 ということにしてやれば,対角行列との内積は 0 になるのだから,(1) 式の条件を楽に満たせることになる.
つまり,対角行列は対角行列だけで (1) 式の条件を満たすようにして,残りの生成子についてはそれらだけで (1) 式の条件を満たすようにしてもいいわけである.分けて考えることが出来る!
対角行列の具体的な条件
では対角行列について,どのような選び方が許されているかについて確かめてみよう.生成子はエルミート行列だからその対角成分は実数で良いわけで,二つの対角行列というのは次のような形である.
対角和がそれぞれ 0 であること,そして,(1) 式の主張通りに,互いに直交していること,自身との内積が 2 になることを満たそうとすると次の 5 つの関係が成り立つことになる.
6 つの変数に対して条件が 5 つあるのだから,自由度が 1 つ残るはずである.例えば
のみで全ての成分が表せる.2 乗が入っているので正負の場合分けが面倒なのだがちゃんと解くことが出来るし,解が実数であるという条件によって各変数の最大値,最小値にも制限が掛かる.
多少面倒なのだが,それほど高度な話でもないので,ここでは計算の途中経過を省略して,結果だけをまとめることにしよう.式で表現するよりも図で表したほうが分かりやすい.という 3 つの組み合わせを作って,これらを 3 点の座標のように考えると,この 3 点は半径
の円に内接する正三角形の頂点になる.
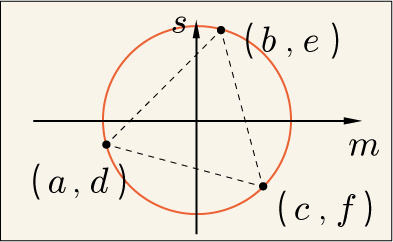
この図ではとりあえず一例を描いてみたが,と
の位置関係が入れ替わっていてもいい.この円上で 3 点が 120°ずつの間隔を保って回転するような位置関係になっている全ての状況が許されることになる.
前にも説明したが,ゲルマン行列の場合には次のようになっていたのだった.
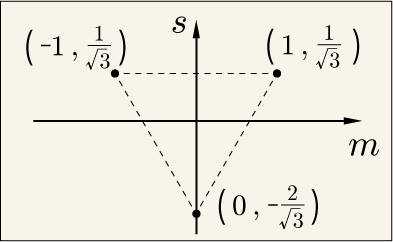
これを「ウエイト図」と呼ぶのだった.このような配置になるのは必然ではなく,許された配置の一例に過ぎなかったというわけだ.
やはりゲルマン行列は数ある許された可能性の中から特別な状況が選ばれているようだ.すると次に生まれる疑問は,ゲルマン行列が代表としてふさわしいかどうかという点だ.このあとの議論でゲルマン行列を使って導かれる話が,ゲルマン行列を選ばなかった場合にも同様に成り立つという保証はあるだろうか?
しかしこの疑問を追求するのはまた別の機会にしておこう.まだ考えることが多すぎて,もう少し状況を整理してみないと取り組めないのである.
ウエイト図の意味の再確認
対角行列の固有ベクトルというのはとても分かりやすくなっており,次のように表される.
これらは 2 つの対角行列の共通の固有ベクトルになっている.一方の行列の固有値は
であり,もう一方の行列の固有値は
である.それぞれこの順で,上に書いた 3 つの固有ベクトルに対応している.
先ほどの図の 3 つの点はこの 3 つの固有ベクトルの存在を意味しており,それぞれの座標はそのときの 2 つの対角行列の固有値の組である.
生成子の固有値の組み合わせはかなり自由に選べる!一つの円上に縛られるし,一方の対角行列の固有値を決めてしまえばもう一方も決まってしまうけれども,連続的に無限に変化させる自由がある!
相似変換で行き来できない自由度
いよいよ,最初の方で話した話題に戻ることが出来る.相似変換というのは,固有値を変えることがないことが証明されているのを思い出して欲しい.(2) 式のような相似変換では,もともとの行列が持つ固有値の組の値を変化させることは出来ないのである.固有値がさまざまな値を取る対角行列の存在が許されているというのに,(2) 式の相似変換ではそのような可能性との間を行き来することが出来ないことが分かる.
つまり,生成子の固有値は連続的な様々な値を取るわけだが,さらにそれらの一つ一つを (2) 式で相似変換させるだけの自由度が存在している.ゲルマン行列を (2) 式で変換させるだけではすべての可能性を表現し尽くせないというわけだ.
ちなみに,同じ固有値の組を持っている行列どうしは (2) 式の相似変換で全てつながっていると言える.なぜなら,あらゆるエルミート行列は相似変換によって対角化できることが証明されていて,対角行列を経由することであらゆる行列へとジャンプできるからだ.その対角行列の成分は固有値を意味しているのだった.複数回の相似変換はひとつの相似変換にまとめることができる.しかも対角行列の成分の並びを変更することも相似変換によって可能なので,固有値の値さえ同じならば,相似変換でつながっているのである.
これで,生成子の選び方のバリエーションがどれくらいあるかというのがかなり見えてきただろう.しかし今は対角行列の自由度を考えてみただけだ.残りの非対角な形の生成子の選び方についてはどの程度の自由度が許されているのだろうか?
固有値はバラバラでいい?
私がこんなことを気にしてあれこれ調べるようになったそもそものキッカケは,ゲルマン行列が持つ固有値が不自然すぎることに気付いてしまったからだった.
は,どれも
という固有値を持つのである.そして
だけが
という固有値を持つ.
なぜだけが仲間外れなのだろうか?そこに意味はあるのだろうか?すごく整いすぎているのに,一箇所だけが恐ろしくいびつだ.
物理との関係を考えていると,固有値というのは量子的現象における観測値と結びつくわけで,その値になることに必然性があるのかどうか,その行列が現実世界においてどんな現象に対応しているのかというのがすごく気になってくるのである.
実は私はこのあたりをまだ完全に調べ切れていない.試してみて分かったことだけを書いておこうと思う.
コンピュータで 8 個の生成子の成分をランダムに生成してみた.この段階で (1) 式の条件は満たされていないが,線形独立ではあるだろう.8 次元もある自由度の中でデタラメに選んだベクトルのようなものがたまたま線形従属になる可能性はかなり低い.
次にこれをグラム・シュミットの正規直交化法を使って直交化してみた.要するに (1) 式を満たすような形に改変を加えてみたということである.これは全く問題なく実行できたし,結果が実際に (1) 式を満たしていることも確認できた.
こうして作った 8 個の生成子の固有値を求めてみた.どんな結果が出たと思う?かなりでたらめな値だった.でたらめすぎて自分には規則性が見いだせなかった.それぞれの行列がそれぞれに異なる固有値を持つ.3 つの固有値が円周上に120°の間隔で並んでいるのではないかという予想も立ててみたが,それさえ成り立っていなかった.
この 8 個の生成子のうちの 2 個を対角行列に固定してその固有値を変えたりしてみたが,あまり影響されている感じもしなかった.それについては既に話したことを考えに入れれば当然だとも言えるだろう.非対角行列の対角成分を 0 にすれば,2 つの対角行列と残り 6 つの非対角行列はそれぞれ独立して直交関係を保ったまま変化させても良かったのだから,対角行列の値に関係なく色んな固有値を持つように選び得るのである.対角行列の選び方によって縛られたりはしないだろう.
以上のことからのとりあえずの結論は次のようである.8 つの生成子が持つ固有値の値は,かなりバラバラに選ぶことが出来る.ゲルマン行列で固有値の値が揃っていたのは偶然であろうし,一つだけ違っていたことについても大した意味はないだろう.きれいな選び方をしたからきれいな値だったのだ.
8 個の生成子は相似変換を使って互いに行き来できるのではないかと思いこんでいる人もいるかと思うが,それぞれの固有値が異なる以上は,それはあり得ない.ゲルマン行列ではだけでそれが可能であるが,たまたまである.
8 個の生成子は 8 次元空間内の正規直交基底のようなものなので,8 次元のユニタリ行列によって基底変換を行うことはできるだろう.互いの立場を入れ替えて行き来するような変換も含まれるだろうが,それとこれとは別の話である.まったくややこしいことだ.イメージがこんがらかる.
私は長い間 8 次元空間をさまよい,こんなことばかり考えていたので,「3D酔い」ならぬ「8D酔い」を起こしてしまった.こうしてこの話を書いている今も,だんだんと気持ち悪くなってきた.今回はこれくらいにしておこう.










