物理数学：二次形式

二次形式

例えば変数,があるとき, のような多項式を「二次形式」と呼ぶ.どの項も 2 次になっているからである.変数が,,の 3 つであるときには, のような項が考えられるだろう.この中の項のどれかがなくてもいい.係数がたまたま 0 だったのだろうと考えればそれで済むからだ.一般には次のように表すことができる. ほらほら,何だか,行列に関係がありそうな雰囲気が漂って来たではないか.係数を表現している $a_{ij}$ の部分は行列で表せそうだ.そこだけではない.この多項式そのものを行列の計算を使って次のように表せるのである. これをもっと簡略に表現すると,こうだ. 変数の組 $\{x_{1},x_{2},…,x_{n}\}$ を縦ベクトルで表して,横に並べたベクトルを転置行列の記号を使って ^t x と表現しているのがミソである.

主軸変換

ここに前回学んだ「対角化」を応用することを考えてみよう.変数 $\{x_{1},x_{2},…,x_{n}\}$ に対して何らかの変換を施してやることで,係数の詰まった行列を対角化するのに成功したとしよう.変換後のの成分には対角成分しかないのだから, という形に変形したのと同じことになる.具体例を挙げれば,次のようなものだ. x'y' や y'z' や z'x' などの「変数が混じった項」のない,すっきりした形に直したということだ.このような形を「標準形」と呼ぶ.

この変換のイメージをグラフで見てみよう.例えば, という式をグラフに表すと,係数によって楕円や双曲線になる.楕円や双曲線などの二次式のグラフの対称軸のことを主軸と呼ぶが,それが傾いた形になるのが普通である.ここでは例として楕円を描いておこう.次のような具合である.

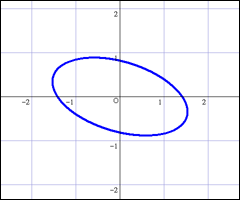
これに対角化を応用して変換した後の式はという形になるが,それをグラフに表すと

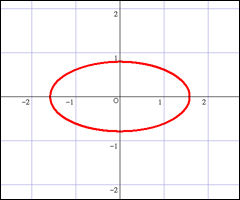
という形になる.これは元の図形を回転させて主軸の傾きをなくした形である.もちろん元の図形が傾いた双曲線であった場合には,変換後には同じ形で主軸が傾いていない双曲線になるのである.それで,このように対角化を利用して一般の二次形式を標準形に変換することを「主軸変換」と呼ぶ.

それを実行するために,どのような手順を踏んだら良いのだろうか？

変換の手順

理論的な方針としては,次のような変換をしてやりたいのだ. 前回やった対角化の考えを使えば,すなわち $P^{-1}AP$ が対角行列になるような行列を求めることができるだろう.そこには問題がない.しかし別のところで問題がある.最後のところでという置き換えをしたわけだが,同時にという置き換えもしている.こんなことが許されるだろうか？もし次のような条件が成り立っているとすれば文句は出ないであろう. 結局のところ,この変形計画はがこの条件を満たす形になっていないと成り立たないのである.行列を作る際には「前回は考慮しなかった何か一工夫」が必要になりそうだ.

この (1) 式の条件を満たす行列のことを「直交行列」と呼ぶ.なぜそう呼ばれているのか,この条件の意味をこれから探ってみよう.

直交行列の意味

(1) 式の意味を考えてみたい.その両辺にをかけてみれば, となって逆行列が消えるからこちらの方が考えやすそうだ.(1) 式と (2) 式は同じ意味である.

まずは簡単な場合で試してみよう.を 2 次の行列であるとして,その成分を次のように表してみる. これを (2) 式に代入してみると, となっており,要するにということらしい.これが何を意味しているかだが,最初の二つの式の形から想像するのは絶対値だ.の中にベクトルが縦ベクトルとして並んでいると考えると,確かにその予想がピタリと当てはまる.各ベクトルの絶対値がどちらも 1 でなければならないことを表しているようだ.では,残るもう一つの条件は何を意味しているだろう？二つのベクトルの内積だ！その値が 0 だというのだから「二つのベクトルは直交しているべし」と言っているわけだ.

行列の次数が増えても同様なことが言える.それについては確かめてみて欲しい.

つまり,(1) 式の条件というのは,行列の中にベクトルが縦ベクトルとして並んでいると見た時に,それぞれのベクトルの長さが全て 1 になっていて,全てのベクトルが互いに直交していることを要求していることになる.

いや,これは困ったな.に入れる固有ベクトルの絶対値をすべて 1 に調整しておくことは少しの手間が増えるだけでそんなにも難しくない.しかし,今まで固有ベクトルが互いに直交しているかどうかなんてことはまるで気にしていなかったぞ.いや,単に気にしていなかったかどうかという話ではない.固有ベクトルが互いに直交してないことは幾らでもあったではないか.それでも対角化をする分には全く問題はなかったのだ.

しかし主軸変換をするためには固有ベクトルが互いに直交していないといけないらしい.それはつまり「主軸変換はいつでも可能だとは限らない」ということになるのだろうか？

対称行列の面白い性質

その点について心配は要らない.二次形式を表現するために使った係数の行列は実は「対称行列」という特別な性質を持った形式で表せる.対称行列というのは,転置行列と元の行列が全く同じという性質を持ったものである. 行列の対角成分を対称軸として見た時に,その両側が対称になっていればそれは対称行列である.

例えば, という二次式を行列で表すのに, のように書いてもいいわけだが,別の書き方もできる.例えばここでは項の係数を表すのに $a_{12}$ だけを使っているわけだが, $a_{12}$ と $a_{21}$ とで半分ずつ分け合うこともできるだろう.他の非対角成分も同様である. このように表すようにすれば,が対称行列となるようにできるのである.

さて,行列が対称行列だとどんな良いことがあるのだろうか.実は次のような定理があるのである.

「異なる固有値に属する固有ベクトルは互いに直交する」

ただしこれは,成分が全て実数であるような対称行列の固有値に限って成り立つ話である.

注意：なぜここで成分が全て実数であることにこだわるかというと,複素数が含まれる場合には内積や直交についての考え方が少し違うので,対称行列ではうまく成り立たないのである.対称行列の代わりにエルミート行列というものを考えないといけないのだがそれは後で話す予定だ.

この定理を証明するのは簡単だ.まず,実対称行列の固有ベクトルから二つを選んで, $u_{1}$ , $u_{2}$ とする.その固有値はそれぞれ $λ_{1}$ , $λ_{2}$ だとすると,次の関係が成り立っている. ここで実対称行列の性質を使いたいので式の両辺を転置して ^t A を作ってみたい.(3) 式にだけそれを試してみる. A = ^t A なのでこの式は次のように書き換えてもいいだろう. この式のの右隣に $u_{2}$ があれば (4) 式を当てはめられそうだ.そこで両辺に右から $u_{2}$ をかけてみよう. こうして両辺の形が似たものとなった.まとめられそうだ. これは $(λ_{2}-λ_{1})$ か $^t u_{1}u_{2}$ かの少なくともどちらかは 0 であることを示している.もし $λ_{2}≠λ_{1}$ ならば $^t u_{1}u_{2}$ の方が 0 に違いない. $^t u_{1}u_{2}$ というのは,成分に分けて具体的な行列計算を考えれば分かると思うが, $u_{1}$ と $u_{2}$ の内積を意味している.つまり内積が 0.固有値が異なる二つの固有ベクトルは直交していると言えるわけだ.

元の話題に戻ろう.要するに,主軸変換を行う際には,導かれてくる固有ベクトルが自動的に直交しているので,何も心配は要らないということだ.しかし固有値を求めるときに重解を含んでいたらどうだろう？同じ値の固有値に属する固有ベクトルどうしについては直交しているという保証はないのだ.その場合はどうしたらいいのだろうか.

グラム・シュミットの直交化法

直交していない複数の線形独立なベクトルがあるとき,それらを元にして同数の互いに直交するベクトルを導く機械的な手続きがある.それを「グラム・シュミットの直交化法」と呼ぶ.

これを使えば,固有値が重解になっている場合でも必ず一定の手続きで互いに直交するベクトルを準備することができる.

元となる個の独立なベクトルを $u_{1},u_{2},…u_{n}$ としよう.そして目標である個の直交するベクトルを $w_{1},w_{2},…w_{n}$ で表すことにする.

まず,最初の一つ $u_{1}$ を取り出し,長さを 1 に調整する.それを $w_{1}$ としよう. 一つ出来上がりだ.

次にこんな計算をしてみる.まだ完成品ではないので仮に ${w'}_{2}$ としておこう. 何をしたのかというと,2 番目のベクトル $u_{2}$ に含まれている, $w_{1}$ と同じ方向の成分を抜き取ったのだ.これで $w_{1}$ と ${w}'_{2}$ とは直交していると言えるだろう.これについても長さを 1 に調整する. これで二つ出来上がり.

次を見れば,この後どうやって続いて行くかは想像できるだろう. 3 番目のベクトル $u_{3}$ から,そこに含まれている $w_{1}$ 成分と $w_{2}$ 成分とを抜き去ったのである.これで 3 番目のベクトルは,すでに出来上がっている最初の 2 つのベクトル $w_{1}$ , $w_{2}$ のどちらとも直交することが言える.これも長さを 1 に調整して正式に 3 番目の完成品として認めてやろう. こんな具合にして,だんだん手間が増えて面倒になるけれども最後まで続けるのである.

理解してしまえば,実に大したことない方法だ.

実対称行列は必ず対角化できる

それでも注意深い読者にはまだ心配が残るだろう.固有値が互いに異なる場合は問題ない.また,固有値が重解を持っていても,独立な固有ベクトルが個あれば問題ないのだった.しかし,固有値が重解を持っていて,個の独立な固有ベクトルが得られなかったらどうなるのだろう？

一般の行列ではそのようなことが起こり得る.しかし実対称行列の場合にはそんな心配は必要ないのである.実対称行列の固有値が重解を持っていたら,必ず独立な固有ベクトルが個だけ得られることが証明できるからだ.

しかしその証明は少々面倒なのでここではやめておこう.

後で複素数の範囲まで話を拡張して,もう少し深い概念を説明してからの方が良さそうだ.実はまだ話していない「正規行列」というものについて同じ内容が証明できるのである.実対称行列は正規行列の一種である.まとめて証明した方が楽だろう.

そう言えば,実対称行列の固有値が必ず実数として得られることについても証明が必要なのだった.これも複素数を導入した方が証明が楽なのである.次の行列の固有方程式はすなわち次方程式である.次方程式は必ず個の根を持つことが複素数の範囲で成り立っている.それらが全て実数として得られるとなれば,今回の心配は全て晴れることになるだろう.しかし実数かどうかの証明は複素数の範囲でやらないと難しい.

とにかく,まだ根拠は説明し切れていないが,実対称行列は必ず対角化できることが保証されているのである.

注意書きなど

「二次形式」とその「主軸変換」は対角化の応用の一例に過ぎない.しかし今回はそれををダシにして行列の重要な性質を色々と説明することになった.「主軸変換」に関する部分とそうでない部分をはっきりさせておこう.

二次形式を実対称行列で表しておけば,必ず直交行列で主軸変換が可能なのだというのが今回の主題だった.

しかしそれは主軸変換に限った話であって,実対称行列をとにかく対角化したいというだけなら,別にわざわざ直交行列を使わなくても必ず対角化は可能である.それでも,直交行列は分かりやすい性質を持っているので,主軸変換をするわけではない場合にでも好んで使われる.

独り言：私は実対称行列は直交行列でしか対角化できないような書き方をしている教科書が気になるのである.

直交行列の図形的な意味を説明しておこう.これは長さ 1 の互いに直交するベクトルを並べて作った行列であるから,これを使って変換しても,元の座標の目盛りの倍率を少しも変化させないし,互いの座標軸の角度も変えない.そのイメージは,ただの座標の回転か,鏡像変換か,両者を組み合わせたものに限られる.鏡像変換というのは,どれか一つの座標軸の方向だけを反転させる変換である.二つ以上の座標軸を反転させたものを考える必要はない.なぜなら,二つの座標軸を反転させたものはその二つの座標軸を含む面内での 180°の回転と同じ意味だからだ.

最初の方に例として描いたグラフでもそうなっている.ただのグラフの回転である.グラフを反転させるかどうかは,直交行列を作る際にどれかの縦ベクトルに -1 をかけるかどうかで決まるだろう.そういう操作をしても縦ベクトルが互いに直交であることには変わりないから気にしなくていい.固有ベクトルの選択次第でどうにでもなってしまう話だ.

「グラム・シュミットの直交化法」は主軸変換に限らず幅広く使われるテクニックだし,実対称行列も直交行列も,主軸変換に関係なく重要なので,その性質を覚えておいて欲しい.