物理数学：線形空間

線形空間の公理

ここまで色々なイメージの助けを借りて説明してきた.連立一次方程式に始まり,座標の変換,そしてベクトル,ついには二次形式の係数にまで当てはめた.ところがそれらの間には時々非常に似通った点が見出されたのだった.表向きのイメージは全く違うものの,これらの背景にある論理そのものは共通なのではなかろうか.行列という表現形式が線形代数の論理の本質を良く表しているようにも思えるのだが,本当にそうだろうか.

数学者の関心は個々の具体的なイメージよりも,その背景にある論理そのものに向いている.一体,これら様々な性質の全ては何を根拠にして導かれているのだろうか.数学者はその必要最小限の根拠から全てを組み立てたいと考えている.そういう「ものごとの根源を知りたい」という点では物理学者の精神と共通したものを感じる.

数学者たちは色々と考えた結果,ここまで語ってきた線形代数の内容の全ては最低限次のような仮定をすればそこから全て導けるということを見出した.

まず集合を考える.これが何の集合であるかについては制限しない.集合の要素のことを専門の数学では「元（げん）」と呼ぶわけだが,この集合の元どうしの和が計算できて,その結果も同じ集合の元になっているとする.また,集合の元に対して定数倍するという計算も許されていて,その結果も同じ集合の元になっているとする.

さて,和については次のような規則が成り立っているとする.

(1)		（結合法則）
(2)		（交換法則）
(3)	「どの元に対しても」となる元が存在する	（零元の存在）
(4)	どの元に対しても「となる元が存在する」	（逆元の存在）
	（そのをと表す）

定数倍については,次のような規則が成り立っているとする.ここに出てくる定数やは今のところ実数だとしておこう.

(5)		（右分配法則）
(6)		（左分配法則）
(7)		（結合法則）
(8)

集合の元がこれらの (1) ～ (8) の条件を全て満たすとき,その集合のことを「線形空間」と呼ぶ.ここでは定数やを実数だとしておいたので,「実線型空間」と呼んで区別することもある.定数やを複素数だと決めておくことも出来て,その場合には「複素線形空間」と呼ぶこともある.どちらに決めても今後の議論はほとんど変わらない.これを元にした証明の内容は,「定数は実数である」と制限している部分を「複素数である」と置き換えるだけで同じ結果が言えることが多い.

教科書で「 $\boldsymbol{R}$ 上の線形空間」と書かれているのは実線型空間のことだし,「 $\boldsymbol{C}$ 上の線形空間」と書かれているのは複素線型空間,「 $\boldsymbol{K}$ 上の線形空間」と書かれているのはそのどちらか,どちらでも,という意味だ.

もう少し正確に言っておこう.実はこのKというのは「体」と呼ばれる抽象的に定義された概念を意味している.それは線形代数の定義とは別のところで議論されている.「体」の具体例としては実数や複素数などがあって,どちらも当てはまるのでどちらを使ってもいいということである.

まだ色々と注釈を加えたいが,それは後にしておこう.

もうひとつだけ,今言わせて欲しい.教科書によっては条件 (3) で述べられている零元が「唯一つだけ」存在するべし,という表現になっていることがあるが,実はこの表現はわざわざ入れなくても良い.もし存在するなら唯一つしかないことは証明できてしまうので入れる必要はないのだ.条件 (4) についても同様で,ある元 x に対する逆元があるとすれば,それは一つしかないことが証明できてしまうのである.

数学の教科書にはこれらのことだけを元にして全てのことを導き出すという挑戦の足跡が誇らしげに記録されているわけだ.初心者にとって数学の教科書が分かりにくいのは,数学者たちの間では当然になっているその文脈が分かっていないことが原因なのではないかと思う.

ここに書かれた条件だけから全ての法則を導き出して行くのだから,この条件を満たすものであれば,それがどんなものであっても,同じ法則を当てはめることができるのである.たとえ,どんなに異なる実体に見えていたとしてもだ.実体にとらわれない証明ができるから,細かな法則を簡潔に表現することもできる.そういうところが抽象化の利点だ.

しかし少し言い訳しておかないといけない.前回までに話してきた内容を全て導くにはもう少しだけ前提が足りなくて,「内積の公理」というものも取り入れないといけない.それを先に説明すると話がややこしくなるので,とりあえずここまでの前提で話を進めよう.

ベクトル空間

数学では今やっていることが何を意味するかについて多くを語らないことが多い.下手な説明を加えることで誤解の元となる余計なイメージを与えかねないからだ.証明されたことが全てであって,それ以外のものを安易に付け加えるべきではないという雰囲気が感じられる.

しかし私はそのような信念には束縛されていないから,多少の不正確さには目をつぶって,分かりやすいと思う説明を好き勝手に加えさせてもらおう.数学のやり方で数学をやりたい人は数学の教科書を読めばいいのである.

先ほど挙げた 8 つの条件「線型空間の公理」が何を意図して組み立てられたものかと不思議に思うだろう.これは「ベクトル」の抽象的なイメージなのである.先ほど集合と書いたが,はベクトルの頭文字である.

線形代数に出てくるベクトルはこの公理を満たしている.一方,物理で使うベクトルは線形代数でいうところのベクトルとは少し異なる性質を持つこともあるのだが,あまり気にするほどでもない.この公理を満たす限りは応用可能である.

物理では,物体の各点に働く力や,電場や磁場の大きさなどを表すのにベクトルを利用する.そういうベクトル量は場所ごとに決まっていて,離れた場所にあるベクトルどうしは何の理由もなく足したり引いたりは出来ないことになっている.まぁ,そういった性質はここで言っているベクトルとは少し違うよね,という程度の話である.世の中には同じ言葉で言い表されているものなら別分野の話であっても全く同じものだと感じてしまう人も多いし,混同しないように細かく分類して違う名前で呼ぶべきだと声高に主張する人も多い.よっぽどのことがない限り,そこまでしなくても問題ない.かえってややこしくなるだけだ.

線形代数に出てくるベクトルは,座標の原点を始点とする多数の矢印をイメージすると分かりやすい.互いに異なるベクトルは,それぞれ矢印の先が異なる位置を表している.このように,位置の座標を指し示すために使うベクトルを「位置ベクトル」というのだった.

数学ではイメージを固定化したくないので,このような「位置ベクトル」という用語はわざわざ使わない.今回の公理を満たすものはどんな実体であってもベクトルなのだ.

あるベクトルが集合に含まれていて,それを定数倍したあらゆるベクトルも同じ集合に含まれているなら,それら全てのベクトルは「ひとつの無限に続く直線」の上に乗っているだろう.この集合の中にはこれ以外に,その直線上にない別のベクトルもあったとする.それを定数倍したものの集まりは別の直線を表す事ができるだろう.このような具合にして,一つの集合の中に異なる直線に乗るようなベクトルがあったとする.それら異なる直線上のベクトルどうしの足し算ができて,その結果も同じ集合に含まれるなら,この集合に含まれるベクトルを全て集めれば,一つの平面を構成することが出来るだろう.このように,集合に含まれるベクトルの一つ一つが原点からウニのように矢印を突き出している.ウニと違うのは,この矢印には短いものも長いものもあり,長いものは無限の彼方を指しているものもあるというところだ.まるでテントを張るかのように,ベクトルの一つ一つが集まって「空間を張っている」ようなイメージだ.

数学ではたとえこのような空想可能な具体的なイメージが成り立たない場合であっても,集合のことを空間と表現することが多い.集合の元が抽象的な空間を構成しているかのようなイメージである.それで集合を「線形空間」と呼んだのである.線形空間は「ベクトル空間」と呼ばれることもある.どちらで呼んでも印象が少し変わるだけであって,内容は同じである.

もちろん我々がベクトルと呼んでいる以外のものであっても,この公理を満たしているものは色々とある.「それをベクトルと呼ぶのは変だろう」というものでも,この公理を満たす限りは,抽象的にはベクトルと言っても差し支えないのである.実際に,線形空間になっている集合の元のことをベクトルと呼んでしまうことは線形代数の教科書ではよく行われている.

次元

物理に応用するための線形代数の性質はすでにほとんど説明してしまったので,数学の教科書のようなやり方でわざわざ最初から全てを説明し直す必要はないだろう.

しかし大学では数学としての線形代数を学んで試験をパスしなくてはならないし,物理で使わないような内容まで試験範囲に含まれることもあるだろう.それで,読者が自力で線形代数を学ぶときに参考になりそうなことを書いて行こう.主要な用語の説明と,大まかな話の流れ,豆知識的なことなどだ.細かいことは専門書に任せれば良いだろう.

先ほどの公理を満たすものの中で,もっともベクトルとして自然に受け入れ易いのは,「数ベクトル」というものだ.個の実数を順序を決めて並べたものである. なるほど,これは「次元ベクトル」として我々が慣れ親しんでいるものそのものである.このような形式のベクトルの集合を R^n という記号で表す.ここで使っている R は実数（Real Number）の頭文字である. R^n のことを正確には「実次元数ベクトル空間」と呼ぶ.

今,次元という言葉が出てきたが,集合の次元というやつをちゃんと定義しておかないといけない.「数ベクトル」の場合にはそれが何組の実数で表されているかを見るだけで分かりそうなことなのだが,違う形式の何か得体の知れないものが線形空間の元になっていることもあるので,そういう場合であってもちゃんと当てはめて議論できるような定義が望ましい.

その為には「基底」というものを先に定義しなくてはならない.結論を先に言えば,その集合の中で選べる基底の数が「次元」だということにしたいのである.「基底」についてはすでにどこかで説明したが,難しくないのでもう一度書いておこう.

前回までの解説では「基底」という言葉が出てくるまでにかなりの話数を必要としたが,抽象的な線形代数では割りと初期に登場させることができる概念なのである.

数学的な正確さを欠いて良ければ一言で言ってしまえる.「基底とは,互いに線形独立であるようなベクトルを一組にして並べたもので,その線形和によって線形空間の全ての元を表すことの出来るものである.」

この意味を把握するためには線形独立の定義も前もってしておかないといけないだろう.それも簡単にできる.ベクトル $\{x_{1},x_{2},…,x_{n}\}$ が線形独立であるとは, という式を成り立たせるためには全ての係数 $\{a_{1},a_{2},…,a_{n}\}$ を 0 にするより他にないことである.これもすでに話したものを少し別の言い方で表しただけだ.

なぜすでに説明した話をわざわざ説明し直したかというと,最初の公理だけからこれくらいのことが問題なく定義できてしまうことを見てもらいたかったからである.

さて,このように定義された基底の数によって,線形空間の次元が定義されるのである.なぜなら,同じ集合の中では基底をどのように選ぼうとしても必ず同じ数になることが証明できるからである.その証明はここではしない.

集合の次元のことを, と表す.

部分空間

線形空間であるような集合があって・・・,いや,わざわざこんな言い方をしなくても「線形空間」と言いさえすれば済むのだが,ここではまだ慣れない読者のためにがただの集合であることを強調したいのだ・・・.ではもう一度仕切り直し.

線形空間であるような集合の部分集合が,もしだけでも線形空間の公理を満たす時,その集合のことをの「部分空間」と呼ぶ.

簡単なものだろ？それだけだ.

線形空間からテキトウに元を幾つか拾い集めて部分集合を作っただけで勝手に線形空間になっているほど甘くはないということだ.線形空間になる条件を満たすためにはある程度考えて元を集めないといけないのである.

集合の部分集合という場合,がそのものである状況も含まれている.だから線形空間の部分空間が実はそのものである場合もありえる.それで dimV≧dimW という関係が成り立っている.

ところで,部分空間の選び方というのは一体どれくらいあるのだろうと感じているかもしれない.無数だ.例えば 2 次元のベクトル空間で考えてみよう.平面のイメージである.その平面内で原点を通る一つの直線を考える.この直線上の点を指し示す全てのベクトルを集めたものは線形空間の公理を満たす.よってそれは部分空間の一つだ.このような原点を通るような直線は他に幾らでもあるから,部分空間の選び方は幾らでもあるに違いない.

3 次元ベクトルを考えた場合には,「原点を通るあらゆる平面」「原点を通るあらゆる直線」が部分空間になる.この場合,部分空間の次元は 2 か 1 だ.部分空間の次元が 3 の場合もあるだろう.それは元の線形空間とそっくり同じものである場合に違いない.

dimW=dimV ならば W=V だと言える.

位置ベクトルでイメージすれば線形空間というのは結構単純なものだ.

和空間・直和

では線形空間の幾つかの部分空間を選んで,それらの元を全て集めて一つの集合を作ったとしたら,それは線形空間になっているだろうか？そんなに甘くはないのである.

部分空間 $W_{1},W_{2},…,W_{n}$ の和集合 $W_{1}\cupW_{2}\cup…\cupW_{n}$ は,部分空間にならない事の方が多い.

そこで「和集合」ではなく,代わりに「和空間」というものを定義する.まずは単純に二つの部分空間で考えてみよう.一方の部分空間 $W_{1}$ の元の一つと,他方の部分空間 $W_{2}$ の元の一つを持ってきて,ベクトルの和を計算する.そのようにしてあらゆる組み合わせで多数のベクトルを作り,それらを元とするような集合を考える.すると,それは線形空間になっていることが証明できるのである.そのような集合を $W_{1}+W_{2}$ のように表し,「部分空間 $W_{1}$ と $W_{2}$ の和空間」と呼ぶ.

今は二つの部分空間で考えたが,同様にして多数の部分空間の和空間を作ることも出来る.それでもちゃんと線形空間の部分空間になっている. さて,このようにして出来たの元の一つ一つを眺めると,確かに $W_{1},W_{2},…,W_{n}$ の全ての集合から元を一つずつ選んで全ての和を取った形になっているのは当然だが,中には必ずしも $W_{1},W_{2},…,W_{n}$ の全てから元を選んでこなくても実現できてしまうようなものが混じっていることがある.そのようなものが一つも混じっていないとき,つまり,の元の一つ一つがどれも $W_{1},W_{2},…,W_{n}$ の全てから一つずつ元を選んで和を取った形でしか表せないようになっているとき,これを「直和」と呼び,次のように表す. それは要するに $W_{1},W_{2},…,W_{n}$ が互いに同じ元を持っていなければそうなるんじゃないか,と思うかもしれないが,少しだけ違う.例えば,同じ面内にある 3 つの方向の異なる直線を考えて,それぞれの直線を意味する部分空間を $W_{1}$ , $W_{2}$ , $W_{3}$ としてみよう.これらは共通してという元を持っている.しかしそれ以外には共通して含まれる元はない.

$W_{1}$ と $W_{2}$ との和 $W_{1}+W_{2}$ を考えると,確かにこれは直和になっている.だから $W_{1}\oplusW_{2}$ と書いても良い.

しかしここにさらに $W_{3}$ を加えた $W_{1}+W_{2}+W_{3}$ は直和にはならない.なぜなら $W_{1}+W_{2}$ を作った時点でその中には平面内の全ての点を表す元が含まれることになっており, $W_{3}$ の元と重複してしまうことになるからだ.

ここでは直線を表す集合どうしの和を例にしてみたが,平面どうしの和でも,平面と直線の和を作っても問題ない.同じような感じに考えることが出来るだろう.

追記 (2024/11/07)：ここでは部分空間を使って直和の性質を説明してしまっているため,次元の異なるベクトル空間どうしの直和の説明が出来なくなってしまっている.次元の異なるベクトル空間の直和は,それぞれのベクトルの成分を一列に並べたものだと考えるとイメージしやすい.n 次元と m 次元の直和は n+m 次元になる.ただしそうして作られるベクトル空間が無限次元になってしまうと直和として扱う上で不都合が出てくるので,有限次元のベクトル空間どうしの有限回の直和のみを考えることになる.

追記 (2024/11/10)：今回の説明のやり方だとなぜ次元の異なるベクトル空間どうしの直和の説明が面倒なのかを補足しておこう.今回はそれぞれの部分空間 W_n の元は全て線形空間 V の元になっており,具体的に表したときに dim V 個の成分で表されたベクトルになっている.直和というのはそれぞれのベクトルの成分を一列に並べたものだというイメージをそのまま使うと成分の数が増えすぎてしまって正しくない.部分空間の次元は dim W_n なのだから,dim W_n 個の基底をうまく選んでやることができる.その基底の線形和を作ればその部分空間内の元を表せるだろう.具体的なイメージとしては,そこで使った係数を並べる形で dim W_n 個の成分を持つベクトルを新たに作ってやることができる.部分空間どうしの直和を考えたいときにはそれらの新たに作ったベクトルの成分を一列に並べたものをイメージすれば良い.こういう話をしなくてはならないので面倒になっているわけだ.

直積

教科書によっては直積というものが出てくることもあるが,直和と記号が似ていて混同するといけないので紹介しておこう.イメージは直和よりずっと簡単だ.

追記 (2024/11/05)：ここで記号が似ていると言っているのは私が勘違いして ⊗ を直積の記号だと思っていたからである. ⊗ はテンソル積の記号であり,直積とは別物である.

二つの線形空間を考える.一方の線形空間 $V_{1}$ の元 $x_{1}$ と,他方の線形空間 $V_{2}$ の元 $x_{2}$ をペアにして, $(x_{1},x_{2})$ のように順序を決めて並べて表したものを考える.このようにして作った多数のペアを元とするような集合は線形空間になっていることが証明できる.

とは言うものの,それは次のような和と定数倍が定義されていると考えた場合の話である. こうして作った集合を「直積」と呼び,次のように書き表す. これは元の集合 $V_{1}$ や $V_{2}$ にあった元とは全く異なる形式のものを元とするような集合なので,「これもまた元の空間の部分空間である」だとかそういうことを考えるような関係ではなくなっている.二つの集合から全く新しいタイプの集合を生み出したことになるのである.

追記 (2024/11/03)：長らく U = V₁ ⊗ V₂ という書き方になっていたのを修正した.この ⊗ という記号を使った書き方はテンソル積を表す記号であって直積とは異なるものである.物理の分野では実際にはテンソル積を行っているにもかかわらず直積と呼ぶ古くからの慣習が残っており,私は混乱してしまっていた.たとえば量子力学の角運動量の合成などの議論で出てくる ⊗ は全てテンソル積であるが,直積と書いてある教科書もまだ時々見かけるので混乱しないように気を付けてほしい.

追記 (2024/11/05)：古くは数学分野でも今で言うところのテンソル積のことを直積と呼んでいた時代があるらしいのだが,用語の整理が行われ,今では直積とテンソル積は全く別の意味になっている.物理ではそのような数学用語の変更を気にせず古い表現を使い続けたため混乱を生むことになっており,最近では改める動きが出てきている.

追記 (2024/11/07)：ベクトル空間どうしの直積は有限回,有限次元に限ればベクトル空間どうしの直和と同型である.要するに,どちらもそれぞれのベクトルの成分を一つに並べて表したものだというイメージである.n 次元と m 次元の直積は n+m 次元になる.このようなわけで,数学的にはわざわざ分けて議論する必要のない余計な概念である.数学分野ではベクトルどうしの直積というものをわざわざ考えたりはせず,もっぱら直和だけを議論するようである.

追記 (2024/11/07)：物理で役に立つだろうと思ってこの節を書いたのであるが,物理の教科書で直積と書かれているものは実は現代数学でいうところのテンソル積であることがほとんどである.しかも数学分野ではベクトルの直積というものはわざわざ扱わないという文化なので,ほとんどこの節の意味を失ってしまった.私の失敗から学んでほしい.しかし物理でベクトルの直積というものが出てくることが皆無だというわけでもない.ベクトルを並べて作った「ベクトルのベクトル」と言えるようなものが出てくることがあり,それはベクトルの直積であると言っても良いだろう.しかし数学者にそれを見せれば,それはベクトルの直和であると言われるに違いない.

追記 (2024/11/07)：ちなみに,n 次元と m 次元のベクトル空間どうしのテンソル積は n×m 次元になるので,そこからも直積とはまったく別概念であることがわかる.

写像の基礎

ここから少し話が広がりを見せ始める.

二つの線形空間を考え,一方の元から他方の元への対応を作ることを考えよう.集合論では,ある集合の元を別の集合の元へと対応させることを「写像」と呼ぶ.今回はベクトルとベクトルを結ぶ関係を考えることになるのであるから,これは行列を導入することに相当している.

公理にだけ基いて議論するなどと強調していた割には,いきなり公理にないような話が脇から出てきたようにも見える.しかしもともと集合という概念を使っている時点で,これまでもずっと公理にない概念を援用してきたのである.それ以外にもこっそり色々な概念が入り込んでいる.実数や複素数とは何なのかという問題や,和や積とはどういう計算なのかという問題は数学の別分野で深く議論されていることであり,それらを当たり前のものとして利用してきたことになる.そういう部分に踏み込むと線形代数どころではなくなってしまうので,ここではあまり気にしないで行こう.

こちらの集合の元から相手の集合の元に向かって線を引くようなイメージで対応を考えることにしよう.こちらの集合の元が相手の集合の元を射撃するようなイメージでも良い.持ち弾はそれぞれ一発ずつ.

これには幾つかのパターンがある.こちら側の異なる複数の元が,相手側の同一のターゲットを狙撃する場合が起こり得る.そのような「無駄撃ち」が一件も起こらず,こちらのそれぞれの元が確実に相手側を一つずつ仕留める場合を「単射」と呼ぶ.

また,これとは異なる判断基準もある.相手側の元を一つも漏らすことなく撃ち抜いた場合を「全射」と呼ぶ.要するに全滅させるのに成功した場合だ.全射であるか否かは,単射であるか否かにかかわらず,どちらも起こり得る.

こうして単射か否か,全射か否か,という分類ができたので,全部で 4 パターンに分類されることになるだろう.特に「単射かつ全射」であることを「全単射」と呼ぶ.ああ,そうそう,こちらの弾が相手に当たらないということは考えないことにする.

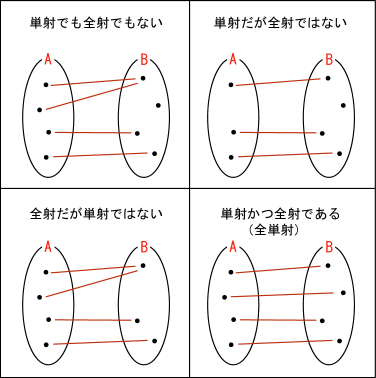
この写像という考えを扱いやすくするために何か記号を用意しないといけない.そこで,例えば集合の元が集合の元を指していることを表すためにという書き方を採用することにする.関数に似ているが,その通り.関数というのは写像の一種である.関数というのは主に数値の対応を示すのに使われているが,写像はもっと色んなものの対応について,たとえ式で表せないような関係であっても,広い範囲で使用できる概念だ.

これから考えようとしているのはベクトルに対してベクトルを対応させるような写像であるから,次のように書くことになるだろう. 文脈によっては元をわざわざ具体的に指定することにそれほど意味がなくて,写像の規則そのものに注意を向けたいときがあり,「写像」とだけ書くこともある.

のことを,写像によるの「像」と呼ぶ.ここではは f(s) と同じものを指しているので, f(s) のことを,写像によるの像と呼んでも同じことである.

教科書によって色々だが,像という用語は他にも幾つかの使われ方をすることがある.部分集合の元の一つ一つを写像で変換した像の全てを集めたものはそれも一種の集合であるが,それを f(W) と書いて「写像による部分集合の像」と呼ぶこともある.先ほどと違って f(W) は集合を表しているわけだ. f[W] と書いてちゃんと区別する場合もある.

また部分集合がどの範囲であるのかが文脈の中ではっきりしている場合には f(W) と同じ意味のことを Im f と表すこともある.というのは像 (Image) の英語を略したものである.教科書のどこにもの範囲を指定している様子がない場合には,考えている線形空間全体に対する像を指していることが多い.

線形写像

線形代数で扱う写像は次の条件を満たしていれば良い.いや,次の条件を満たすような写像を考えるのが線形代数というものだ,ということにしておく.

(9)
(10)

この条件を満たす写像を「線形写像」と呼ぶ.この条件を課するだけで,前回までに使ってきた行列と同じ性質が実現できるのである.いや,まだ少し足りないかな.今から話そう.

ところで,次元のベクトルから次元のベクトルへの変換は行列の行列によって表すことが出来たのだった.しかし同じタイプの行列の行列であってもその中身の数値は様々なのであった.行列というのは線型写像の具体的なイメージであって,写像についてもこれと同じ事が言える.

つまり,先ほどから線形写像をという文字で表してばかりいるのだが,線形写像はもちろん一つきりではない.一口に「集合から集合への線形写像」と言っても,色々な変換の仕方をする「線形写像」が無数に存在しているわけだ.

線形写像の他にも色んな線形写像を用意してやって,例えばその一つをとでも表そう.そして次のような線形写像どうしの計算を定義してやる.

(11)
(12)

このような (f+g) や (af) で表される線形写像を無数に用意してやることも可能だ.これは行列どうしの和や,行列全体の定数倍という計算によって別の行列を作ることに相当する.

さて,ここから話が予想外の方向へジャンプする.

集合の要素としては何をそこに入れるかには制限はないので,「多数の線形写像を集めた集合」というものを考えてやることも出来るだろう.ちょっとややこしい話だが耐えてもらいたい.上の (11) (12) のような計算が成り立つ「線形写像を集めた集合」は線形空間の公理を満たしている.なんと,線形写像そのものがベクトルだというのである！

具体的なものをイメージすれば,そんなにややこしい話でもないのかも知れない.例えば 2 行 2 列の行列というのは行列どうしの和や定数倍というものが計算できる.しかも 4 つの成分のうちの一つだけが 1 で残りの 3 つは 0 だという行列を 4 種類用意できて,それらは基底になっていることが分かる.あらゆる 2 行 2 列の行列はその 4 つの基底を使って次のように表すことが出来るからだ. 4 つの基底がある・・・.つまり, 2 行 2 列の行列は 4 次元のベクトルと同じ構造のものだ,と言えるのである.

もちろん,基底の選び方はこの他にも幾らでもあるが,これが一番シンプルだろう.

双対空間

線形空間の元であるベクトルの一つ一つをいずれかの実数へと対応させるような線形写像を考えてみる.ベクトルを実数へと対応させる写像・・・.別に,何もややこしいことは無さそうだ.そのような写像は幾らでも違ったパターンのものを作ることができるだろう.

そういう無数の写像を集めて集合にしたものも線形空間であって,写像の一つ一つはベクトルのようなものであるという話を先ほどした.このような「線形写像の集合」のことを,「線型空間の双対（そうつい）空間」と呼び, $V^{*}$ という記号で表す.

「双対空間」は「双対ベクトル空間」とも呼ばれる.双対空間の元である写像のことを「双対ベクトル」と呼ぶこともある.

双対というのは「互いに裏返しの関係になっている」というような意味だ.なぜそのような名前が付いているのだろうか.こんなものに,何か特別な性質があるのだろうか？イメージはとても簡単である.

線形空間が次元だとしよう.そしてただの実数というのは 1 次元だ.1 次元のベクトルのことをスカラーと呼ぶのだが,つまり,次元のベクトルをスカラーへと変換することを考えているのである.次元のベクトルからスカラーへの変換は 1 行列の行列として表される.

先ほど話したことによれば,行列というのはベクトルと同じ構造なのだった.1 行列の行列というのは次元のベクトルと同じ構造だと言える.つまり,線形空間に含まれるベクトルも, $V^{*}$ の元である線形写像も,その正体はどちらも次元のベクトルなのであり,対等なのである.

それだけではない.双対空間 $V^{*}$ にとっての双対空間 $(V^{*})^{*}$ は元のである.こういうことが言えるからこそ「双対（そうつい）」なのだ.なぜそう言えるのか,そのイメージを説明しよう.

線形空間内の個々のベクトルは,自分がどの実数へと飛ばされることになるのか,写像に出会うまでは分からない.どのベクトルをどの実数に対応づけるかという全ての情報は写像の側が持っているからである.ところが写像の側から見てみよう.個々の写像にとって,これから来る相手のベクトルをどの実数に飛ばすことになるのか,実際のベクトルに出会うまで分からない.やってきた一つのベクトルによって,待機している全ての写像に対して何かしらの実数がそれぞれに決まるのだから,一つのベクトルによって全ての写像が指し示すべき実数を決めてもらったようなものだ.このように互いの立場は全く対等なのである.

今は飛び先が実数だということで話をしたが,これを複素数に変えてみてもほとんど同じ論理である.ただし複素数は成分が実数部分と虚数部分とで二つあって 2 次元なので,今の話に出てくる次元が全て 2 倍になるという違いがある.

このような話は物理では量子力学に出てくることになる.後で量子力学を学んだ時にでも思い出してもらえばいいことだが,ケット・ベクトルというのは実はブラ・ベクトルに対する双対ベクトルになっているのだ.ブラ・ベクトルとケット・ベクトルとで特別な内積を計算した結果が複素数になるのだから,ブラ・ベクトルを複素数へと結びつける写像の役割をケット・ベクトルが果たしているというわけだ.別にそういうことを知っていなくても,計算ルールさえ知っていれば量子力学の計算をするには差し支えないのだが,知っていればより広い見方が楽しめるだろう.

核・商空間

線形写像によって相手の集合の零元（ゼロベクトル）へと飛んでしまうような元の集まりを「核」と呼ぶ.それを Ker f と表現する. Ker は核（kernel) の略だ.

Ker f もまた線形空間になっている.そう言えば, Im f も線形空間になっているのを言い忘れていた.これらは簡単に証明できるが,面倒になってきたので省略しよう.

こういう概念がどうして重要であるかは数学の教科書を読んでもらった方がいい.色んなことを証明するときに役に立つのだ.すでに物理に必要な結論についてはほとんど書いてしまっているので,説明する必要も感じない.

あとは,「商空間」というものが線形代数の教科書に時々出てくることがあって,初めて学ぶ時に訳が分からなく感じることが多いと思う. Ker f のことをなぜ核と呼ぶのかについては「 Ker f による商空間」を考えるとイメージしやすいのでここでついでに説明しようかと思っていたのだが,物理とほとんど関係がないような気がしてきたので諦めよう.ちゃんと分かりやすく説明するにはもう少し話を広げないといけなくなるのだ.

気が向いたら,つまり,もしすごくうまい説明を思い付いたら,ここに書き足すことにする.

線形代数のすすめ

こうして,線形代数の教科書に出てくる難しそうな用語のほとんどをざっと説明し終えた.本当は内積空間の話もしようと思っていたのだが,思っていたより長くなりすぎたので次回に回そう.

私が大学で初めて線形代数を学んだ頃には,何のための学問であるのかさえ分からなかったし,知らされることもなかった.教科書に出てくる用語も,記号も,関係式も,高校までの数学とは全く違っているように見えた.一応,記号の定義を探そうとはしてみたが,その説明すら理解できなかったのだった.数学の文化というものがさっぱり分かっていなかった.

それは私にとって全く異質の文化であって,把握するまでにかなりの時間が流れてしまった.今回ここに書いたくらいのことを予め知らされていれば,やる気が失せることはなかったのではないかと考えている.

少し分かった気になってもらえたなら,勇気を出して線形代数の教科書を開いてみてもらいたい.ここで紹介しきれなかった色んな関係があって,それらが導かれてくる様子が,ずっと詳しく,じれったいほどに一つ一つ説明されていることだろう.文化が分かれば,なぜああいう不親切にも思える書き方になっているのかと不満を感じたりせずに,むしろ楽しめるだろう.

修正履歴

(2024/11/03)
　・直積を表す記号として U = V₁ ⊗ V₂ という表し方にしていたのを修正.これについての説明を追加.

(2024/11/05)
　・直積と直和の記号が似ていると書いていた部分について,勘違いだったことについての説明を書き加えた.
　・物理でテンソル積を直積と呼ぶことについて「悪い慣習」と書いていたが,無知からのものではなく歴史的な経緯によるものなので「古くからの慣習」と書き換えた.

(2024/11/07)
　・次元の異なるベクトル空間どうしの直和,直積についての補足説明を追加した.

(2024/11/10)
　・ここでの説明方法だと直和の簡易なイメージを説明するのが面倒になるという理由について書き加えた.