内積空間
さて,物理に関係してくるような話に戻ることにしよう.とは言っても今回の話もかなり数学寄りなのだが.
「線形空間」は単純なようでいて,調べてみると色々な構造を見出すことができる.そこに「内積の公理」を加えることで,物理で扱うベクトルにさらに近い性質を持たせることが出来る.ベクトルどうしの角度などの概念を議論することが出来るようになるのである.
二つのベクトル,
を組み合わせたものに対して,実数または複素数の値を対応させ,それを
と表し,内積と呼ぶことにする.内積は次のような性質を満たすようなものだという公理を定めることにしよう.
| (1) | (正定値性) | |
| (2) | (対称性) | |
| (3) | 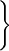 (双線形性) (双線形性) | |
| (4) |
このような内積が導入された線形空間を「内積空間」と呼ぶ.「計量線形空間」,「計量ベクトル空間」,「前ヒルベルト空間(プレ・ヒルベルト空間)」などと呼ばれることもある.「自分の教科書には内積空間なんて話は載ってないよ」と思ったら別の言葉で探してみると見つかるかも知れない.
この (1)~(4) の内積の公理はちょっと説明なしでは分かりにくい性質ばかりだ.我々が良く知っている内積というのは次のようなものではなかったか.例えば二つの 3 次元ベクトルがあって,その成分が
のように表されるものだとしたら,
と計算するのであった.ここでは
と書いたが,上に書いた公理の中では同じものを
と表現している.実は (5) 式のような計算で導く内積は (1)~(4) の性質をちゃんと満たしているのである.
では逆に (1)~(4) の条件さえあれば,(5) 式のような計算の仕方だけが導かれてくることになるのだろうか?そうとは限らない.この条件だけでは少しばかり奇妙なものも許されてしまうのである.とは言っても,これらの条件は肝心なところをちゃんと押さえているので,それほどめちゃくちゃなものが許されるわけでもない.どんなものが許されるのかについての一般的な議論は後でしよう.
軽く考えてみるに,例えば,(5) 式のような計算をする前に一方のベクトルだけを定数倍しておくだとか,最終的な結果に何か定数を掛けたりするくらいのことなら許されるだろう.しかしどちらにしても結果としては内積の値が何倍かされるくらいのことでしかないか・・・.最後に対数を取ったりなんかすると (1) の条件から外れてしまうことになるし,ひどく奇妙な例は作れそうにない.
そもそも我々が慣れている (5) 式のような幾何学的な内積の計算は「数ベクトル」どうしだけで実行できるものである.この「内積の公理」はそのイメージに合うように,内積の持つ本質的な性質だけを抜き出したのである.線形代数で言うところのベクトルというのは「数ベクトル」だけだとは限らない.数学者たちは,この性質さえあれば内積の他の性質を導くのに不都合はないと判断したわけだ.
では (1)~(4) の条件に説明を加えてゆくことにしよう.
対称性について
これまではずっと実数のみを扱ってきたが,上で紹介した「内積の公理」は複素数の可能性も考えたものになっている.内積の値が複素数であっても使えるバージョンだ.
条件 (2) に星印が付いているが,これは複素共役であることを表している.例えば内積が複素数の値を持っていて
と表せるとしたら,その複素共役というのは
ということである.数学では複素共役を表すのに
という書き方を使う事が多いのだが,ここでは物理のための数学ということで,物理でよく使う
という書き方を採用している.
もし内積の値を実数だけに限るとしたら星印を付けても付けなくても値は変わらないので,条件 (2) は
と書いても構わない.幾何学的な内積の計算はベクトルの順序には関係ないということを意味している.よく知っている通りだ.しかし複素数を許す場合には順序によって結果が変わるのである.
なぜそのような公理を採用しているのかについては,この後の話を聞きながら探ってみてほしい.
正定値性について
内積の重要な性質の一つは,自分自身との内積を計算した時には正の値になるというものだ.これは 条件 (1) で表されている.内積の値が複素数になることを許す場合であっても,自分自身との内積を計算した結果に限っては正の実数にならなくてはならない.
複素数についてはそのままでは大小関係を議論することが出来ないから,このように決めておくのは色々と都合がいい.
こうすることで「ベクトルの長さ」に相当する概念が導入されて,ベクトルの大小関係を議論できる.次のようなものを定義すればいい.
これは「ノルム」と呼ばれるものだが,多くの場合これは「ベクトルの長さ」そのものなので「ベクトルの長さ」と呼ばれることも多い.
何とかして内積の公理を満たしながらも通常の内積のイメージを崩すようなおかしな計算が作れないものかとひねくれたことを考えてみるのだが,うまい具合に防がれている.内積の片方のベクトルを定数倍したら,内積の値も同じだけ倍されるという (3) の条件があるので,長いベクトルのノルムはやはり大きな値になるわけだ.ノルムはベクトルの長さを反映する量としてしっかりと機能している.
他の性質を導く
内積の公理の中の条件を組み合わせることで,そこに直接には表されていない性質を導くことが出来る.例えば,条件 (3) の両辺にある内積をどちらも条件 (2) に従って順序を書き換えれば,
となるであろう.複素共役のさらに複素共役を取ったものは元に戻るので,この両辺の複素共役を取ってやれば,次のようになる.
この辺りの式変形にもし疑問があるようであれば,続きを読む前に複素数の基本的な性質を学んできて欲しい.この先では積極的に複素数を導入して色々とやりたいことがあるので,これくらいの変形はまだ基本である.
さて,こうして条件 (3) に似た性質が導き出されたわけだが,このままの形では (3) 式と随分違うような印象を受けてしまうかもしれない.ここで使っているベクトルの記号は別に何でもいいので,(3) 式に似せるように書き換えてしまおう.
(3) とは似ているが,少し違っていて対称的だろう.もし内積が実数に限るとすると,この変形はもっと簡単に終わらすことが出来て,次のような形になる.
これは内積を計算するどちらかのベクトルをどちらでもいいから定数倍すれば結果も定数倍されるという,直観にも合う性質であろう.ところが複素数を許すと,そうではなくなるというのだ.実数倍するときには違いはないのだが,複素数倍しようとすると,それをどちらのベクトルに掛けるかによって結果が違ってくるのである.
さて,条件 (2) と条件 (4) を組み合わせることでも同じようなことができる.こちらは内積の値を実数に限ろうが複素数だろうが次のような式で表せる性質を導くことが出来る.結果だけ書こう.
公理の表の中に書いてある「双線形性」というのは,このようにどちらのベクトルに対しても線形性が成り立っている性質のことを言っているのである.
物理との違い
ところで,すでに量子力学に慣れている読者にとっては上の (6) 式で表される性質に違和感を覚えたのではないだろうか?条件 (3) と (6) 式をもう一度並べて書いてみよう.
数学における内積の性質としては確かにこれで合っているのだ.しかし量子力学においては,これとは少し違う,次のようなルールが採用されている.
二つのベクトルの役割が逆になっていて,内積の右側にあるベクトルが通常のベクトルとして扱われており,左側に書かれるベクトルが「鏡の世界のベクトル」のような扱いになっている.物理では量子状態を表すベクトルを式の右側に置いておきたいという事情があってこうなっているのである.
この違いによって本質的には何も変わらないのではあるが,数学と物理とでこういう流儀の違いがあるということだけ,混乱がないように覚えておいてほしい.
一般的な内積の計算
さて,公理に従うような内積の一般的な形というのは,どのようなものだろうか?そこをはっきりさせておかないと,何かひねくれた内積が入り込む余地がないものかと気になって仕方がない.
実は線形空間の性質を使えばそんなに難しくもないのである.線形空間では基底を選択することによって任意のベクトルを線形和として表すことが出来るのだった.二つのベクトルを共通の基底を使って次のように表してみよう.
これを
に代入して,公理にしたがって変形してみるのである.
途中を省略してすぐに結果を書いてしまったが,そんなに説明が要るほど難しい話でもないだろう.さて,中途半端で終わっている感じもするが,残念ながらこれ以上は変形できない.これが内積の公理から導かれる内積の,一般的で具体的な姿なのである.
高校の幾何学で習うような内積というのはデカルト座標を前提としている.それは「互いに直交していて長さが 1 であるようなベクトル」の集まりを基底として選択して,それを基準にベクトルを表していたことになる.つまり次のような関係を前提としていたわけだ.
この関係を今導いた結果に当てはめてみると,
となる.もし
や
が実数だとすれば
が付いていようがいまいが関係ないので,
となり,(5) 式と同じ形の内積の計算がちゃんと出てくるというわけだ.
もし基底が互いに直交していなくて,長さもそれぞれに異なる場合にはどうなるのだろうか?それはデカルト座標(直交座標)ではなく,座標軸が斜めに交わるような状況である.そういうのを斜交座標と呼び,相対論などではそういう状況を扱うことになる.しかしここでは深入りはしないでおこう.
複素ベクトルの内積
ベクトルの成分が複素数で表されている場合には,(7) 式を使って内積を計算するのである.つまり,一方のベクトルの成分だけ複素共役を取ってから,通常の内積を行うように計算すれば良い.もちろん,長さ 1 で互いに直交している基底を採用しているという前提である.
ただし先ほども注意したように,物理の場合には (7) 式とは逆である.例えば二つの 3 次元複素ベクトルがあって,その成分が
のように表されるものだとしたら,
と計算することになる.物理で使うといってもこんな道具を使うのは量子力学くらいのものだが.
自分自身との内積を計算すると
となるわけだが,複素数
とその複素共役
との積
はいつでも複素数の絶対値
の 2 乗になるという性質があるので,上の計算は各項が必ず正となり,(1) の条件をちゃんと自動的に満たしている.よく出来ているものだ.
二つの複素ベクトルの内積が 0 になる場合,それらの複素ベクトルは直交する,と表現する.複素数のベクトルを具体的にイメージするなんてことはほぼ不可能なんじゃないかと思うが,幾何学のイメージを借りてきたのである.こうして実数の場合にも複素数の場合にも「ベクトルの直交」というものを定義することが出来た.
直交補空間
内積の公理を取り込んだことで直交が定義された.そのお陰で新たな概念を定義することが出来る.
まず,線形空間を考える.その部分空間である
を考える.
に含まれる全ての元と直交するような元を線形空間
の中から全て探してきて,それを集めて集合を作る時,その集合もやはり線形空間になっていることが言える.それを
の「直交補空間」と呼び,
という記号で表そう.
複素ベクトルを考えるとイメージは難しいが,実数に限ればかなり単純なイメージである.
例えば 3 次元空間をイメージする.この中で軸を考えると,この軸上の点を表すベクトルを集めたものはこの 3 次元空間の中の部分空間である.この直線上のベクトルの全てに直行するベクトルと言えば,
平面上の点を表すベクトルしかないだろう.つまり
平面が
軸の直交補空間だというイメージだ.
立場を反対にした話もできる.平面という 2 次元空間は 3 次元空間の部分空間だが,その直交補空間は,
軸上の 1 次元空間だろう.
前回やった直和を使えば次のような関係が成り立っていることも言える.
こういう単純な話なのだが,抽象化して表現しておくことで複素ベクトルにまで同じ論理で議論を進めることが出来るのである.
これで最後の話に突入する準備が整った.











ちょっと説明に困った。