(質問者)ミンコフスキー時空というのは時間と空間が同等に扱われていないと思います.仮に時間と空間を同等に扱うような時空があったとするとどんな世界になるでしょうか?
ミンコフスキー時空というのは 4 次元時空の任意の 2 点間の距離(の 2 乗)を次のように定義する 4 次元空間です.
おっしゃるとおり,時間に関係する項だけ符号が逆になっていて,空間の 3 次元とは別の扱いになっています.試しにこの最後の項の符号を他と同じにして,次のように定義した時空を考えれば時間と空間に区別がありません.
これはユークリッド的な距離の取り方なのでイメージしやすいと思います.
(質問者)はい.そのイメージはよく分かります.しかし時空を対等に扱う距離の定義は (2) 式であるとは断言されませんでしたね.「試しに」などという慎重な表現をわざわざ使っておられる気がしました.ひょっとして時空を対等に扱うような距離の定義の仕方が他にもあるということでしょうか?
バレてしまいましたか.距離を定義するというだけなら時空を対等に扱うやり方は他にもあります.(2) 式のようなユークリッド的な距離の場合は各成分の差の 2 乗平均を使っていますが,2 乗しないで各成分の差の絶対値を足し合わせる「マンハッタン距離」や,3 乗平均や 4 乗平均,5 乗平均,……,その無限の極限を考える「チェビシェフ距離」などもあります.あるいはもっと複雑にして各成分を掛け合わせるような定義を採用することができるかもしれません.ところが,このような距離の定義を一般相対性理論に拡張して使うところまで考えると,複雑な定義は全く無駄になるのです.
一般相対性理論では (1) 式のような距離の定義を「計量テンソル」と呼ばれる行列の形に表して,そこからのズレを考えます.計量テンソルを使うのは,一般相対性理論が採用しているリーマン幾何学がそれを必要としているからですし,そのイメージとしては 2 乗平均距離を使えば十分なのです.しかも計量テンソルの定義からして,直交座標を使っているときには対角成分以外は 0 になります.つまり,成分どうしを複雑に掛け合わせるような定義を使う理由もありません.
そういうわけで,相対性理論の文脈で言えば時空を対等に扱うような距離の定義は (2) 式だけだと言えます.実際は (2) 式はこの宇宙では成り立っていないものなので一般相対性理論で使ったりはしないわけですけれども.こういう「特殊相対論」の話題を越えた面倒な話に入り込まないようにしようとして曖昧な言い回しをしてしまいましたが,しっかりツッコミを入れてくださったお陰でスッキリさせることができました.
(質問者)(2) 式を使ってまともな理論が作れるのでしょうか?
はい.この宇宙とはまるで違う性質を持つことを意味する式が出てきますからまともかどうかは分かりませんが,それなりに辻褄の合った理論式が導けます.ミンコフスキー時空を元にしてローレンツ変換の式を導くのと同じやり方です.1 箇所の符号が違うだけですし,手順もほとんどそのままです.途中で利用することになる物理的な仮定も全く同じです.
ざっと計算内容を説明しておきましょう.(2) 式で表されているは任意の 2 点間の距離の 2 乗ですが,とりあえずは原点からの距離の 2 乗
が変化しないような座標変換を導くことにします.最終的に導かれる座標変換は,原点からの距離だけでなく,任意の 2 点間の距離も変化させないような座標変換であることが確かめられます.計算を楽にするために空間を 1 次元だけにして,
と置けば
は次のように表せます.
そして,次のような座標変換を仮定します.
変換後にも
という関係が成り立っているべきだと考えるので,(4) (5) 式を (6) 式に代入してやって (3) 式と比較することで次のような条件式が導かれるはずです.
具体的な式変形や条件を追加するところは省略しますが,次のような結果が得られるはずです.
(質問者)ローレンツ変換とそっくりな形ですね!符号が何箇所か違っているのが分かりますが,それ以外はよく分かりません.この変換は何を意味しているのでしょうか?
確かに式を見ただけではピンと来ませんが,図にすればとても分かりやすいです.この「ローレンツ変換もどき」の変換では面で原点を中心にした文字通りの回転が起きているだけです.距離が変化しない座標変換と言えば,座標の回転か,座標の反転くらいしかありませんから,まさにそのようなものが導かれてきたという感じになっています.
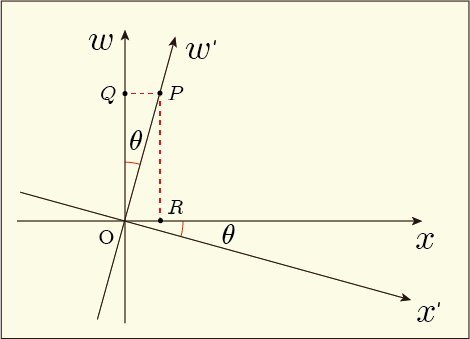
軸は
軸に対して
だけ傾いていますが,
軸も
軸に対して同じ方向へと傾いています.本当にこの変換式にそのような意味があるかどうかを確かめてみましょう.このような回転変換は次のような式で表されます.
軸は
の時に原点にあった物体が速度
で右方向に移動するときの軌跡を表しています.点 P はその直線上の点なので,例えばこれが
秒後の点だとすると
,
になります.
これを頼りに
や
を計算すると次のようになります.
これらを (12) (13) 式に代入すれば,(10) (11) 式と同じになります.式の形は少々複雑に見えますが,解釈してみるとこのような単純な意味になります.
(質問者)物理的にはどんなことが起きるのでしょうか?
ローレンツ短縮とは逆の「運動する物体の長さが進行方向に伸びる」という現象が起きます.相対性理論のような光速の制限はなくて,無限の速度まで加速できます.しかも速度が上がれば上がるほど質量が小さくなったかのように振る舞います.
光に追い付くことすらできるので,この世界での定数は光速という意味を持ちません.光は速度 0 になることもあります.このような世界では我々が知っているのと同じ形の電磁気学は成立しないと思います.
エネルギーと運動量の関係は次のような式で表されます.
この両辺の平方根をとって右辺をテイラー展開すると,質量エネルギーの項と運動エネルギーの項の符号が逆になって出てきます.運動エネルギーを正の値として考えるのが普通の感覚なので,質量エネルギーの方がマイナスだと結論せざるを得ません.つまり,質量は負のエネルギーを持つことになります.
我々の世界とはかなり違った世界になりそうです.これらは通常の特殊相対論の議論をそのままなぞることで全て導けます.
 クロックワーク・ロケット |
このような宇宙がもし存在するのならそこではどのような現象が起こるのかをかなり細かい部分まで考察して書かれているSF小説です。
「<直交>三部作」と呼ばれています。 各巻のテーマは以下の通りです。 第1巻「特殊相対性理論」 第2巻「量子力学」 第3巻「一般相対性理論」 ネタバレしないようにこれ以上のことは書きませんが、今回の話はすでにかなりネタバレになっているかもしれません。 |
このような宇宙が実現する可能性があったのかどうか,あるいは我々とは別の宇宙で実現しているのかどうかは分かりません.さらに物理学が進歩して,我々の宇宙がミンコフスキー時空的であることが論理的な必然であることが分かってこれば,今回のような話は全くの机上の空論ということになるのだろうと思います.










