ロー出し、ハイ受け
ちょっと大きめの電子回路は,あるモジュールの出力を別のモジュールの入力へと繋いでやって,次々と信号を加工して望みの結果を得る構成になっている,という話をしたことがある.このときに注意すべきことについて話しておこう.
出力と入力の関係をごく単純化して表すと,次のようになっている.
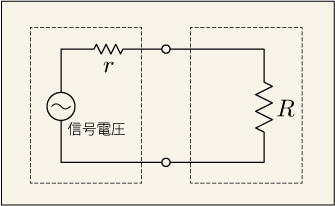
二つのモジュールを繋いだ様子を表したものである.電源はこれとは別に要ることもあるし要らないこともあるのでこの図では省略されている.左側の抵抗は,信号を出力する側のモジュールの内部抵抗のようなものであり,「出力インピーダンス」と呼ばれる.これは単純な抵抗器ではなく,電流を妨げる様々な要因をひっくるめて抵抗の記号で表してみただけのことである.信号の周波数によって抵抗の大きさに違いが出たり,位相にずれが生じたりする場合もあるので,抵抗よりも広い意味を含む言葉を使った方がいい.それで「出力抵抗」ではなく「出力インピーダンス」という表現を使っているのだ.
右側にある抵抗は信号を受け取る側のモジュールの,入力端子側から見た時の「回路内部の抵抗的な要素」をひっくるめて表したものである.これもやはりインピーダンスと呼んだ方がいい.こちらは「入力インピーダンス」と呼ばれる.もしこの
がスピーカーやモーターや LED や豆電球などであって,これに電気を流すことが回路の最終的な目的である場合には,この
のことを「負荷抵抗」などと表現することも多い.
いくつかの例外はあるのだが,基本的には,出力インピーダンスは小さければ小さいほど良くて,入力インピーダンス
は大きければ大きいほど良い.いつでも思い出せるように,図もそういう感じに描いておいた.どうしてなのかを今からざっと説明しよう.
左側に描かれている信号源は,信号の波形を電圧の変化で表現している何らかの回路をたとえたものである.もし電流がほとんど流れていなければ出力抵抗での電圧降下はほとんど起きないので,接続端子間にはこの信号源とほとんど同じ電圧が来ることになる.それはすなわち,負荷である抵抗
の両端に,ちゃんと波形の電圧が正確に伝わることを意味する.
しかし電流が流れていれば,この出力インピーダンス
の部分で
だけの電圧降下が起き,その分だけ差し引いた電圧が負荷
の両端に現れることになる.この
がただの抵抗だったならまだマシな方だ.信号電圧が上がろうが下がろうが,同じ割合で少々下がるだけだからである.しかしインピーダンスが周波数によって違っていたりすると,色んな周波数成分が混じった複雑な出力の波形は,元の信号とはかなり違った,崩れた形になってしまうだろう.
が小さければその影響はかなり抑えられるのである.
さて,電流が流れるほど内部抵抗のせいで電圧が下がるというのだから,右側に繋ぐ回路は電流をなるべく食わないようなものが望ましい.抵抗
が大きければ大きいほど,入力端子は電流を吸い込まないようになる.電圧で表現された信号波形を受け取るために,電流が流れることは必ずしも必要ではない.電流がほとんど流れなくとも,電圧の変化をきちんと受け止められる回路が喜ばれるのである.
この図では簡略化しすぎて,と
が直列になっているため,結局,合計のインピーダンスは
であるように見えるし,それが大きければいいのか小さければいいのか一体どっちだ,と言いたくなってしまう.しかしその見方は重要ではない.ここでは,信号源の電圧が抵抗
の両端にどれほど忠実に伝達されるかが重要なのである.だから,
はなるべく小さく,
はなるべく大きく,だ.
要するに,左側(出力側)は,たとえ電流が多く流れても,容易に息切れを起こしたりせず,信号波形が乱れないようなものが望まれており,右側(入力側)は不必要に電流を要求しないような回路が望まれているというわけである.
信号を出す側は低いインピーダンスで,受ける側は高いインピーダンスで.このことを短く表現して,「ロー出し,ハイ受け」などと言われる.
一旦まとめ
念の為に短くまとめておこう.
今のような文脈で話される場合,出力インピーダンスというのは,出力波形を崩したり電圧を下げたりすることがないままで,電流がどれだけ多く取り出せるかという出力装置の能力を示すものである.出力インピーダンスが小さいほど,その能力が高いということである.電池の話をした時の内部抵抗と同じようなもので,色んな影響をひっくるめた仮想的な概念である.
一方,入力インピーダンスは,どれだけ電流を食わない装置であるかを表すバロメーターのようなものである.
インピーダンス整合
ここからが今回の本題である.上で話したのは,電圧の変化を使って信号をやりとりする場合の話だ.無駄に電力を消費しないように,電流をなるべく流さないことを理想としていたのだった.
ところがスピーカーなどを動かそうとする場合にはまるで話が違う.スピーカーから大音量を得るためには,スピーカーの部分で「なるべく電力を消費して欲しい」のである.電圧だけではだめで,電力を伝達したいのだ.
負荷の部分でなるべく電力を消費してもらうためにはどうしたらいいかを考えよう.直感に反することだが,負荷抵抗が小さいほど「重い負荷」だと表現される.なぜなら,電圧が同じなら,抵抗が小さいほど電流が多く流れるからだ.電力というのは電圧と電流の積で決まるから,電流が多いほど電力をバカ食いすることになるというわけだ.
100 W 電球と 10 W 電球とでは,どちらが抵抗が大きいでしょう?というクイズが良くある.100 W 電球は 100 V に繋いだ時に 1 A 流れて欲しいのだから,100 Ω だ.10 W 電球は 100 V に繋いだ時に 100 mA 流れて欲しいのだから,1 kΩ だ.このように,電圧が同じならば抵抗が小さい方が激しくエネルギーを消費するのである.電球というのは抵抗の部分で電気エネルギーが熱エネルギーに変わることを利用しているのだが,抵抗が小さいほど消費が激しいというのは少し意外な感じがする.
ではが小さければ小さいほど良いかといえば,そうではない.あまり小さいと電流が多く流れ,そのせいで出力インピーダンス
の側での電圧降下の方がずっと大きくなってしまって,肝心な
の両端の電圧が下がってしまうからだ.結局,どうなるとちょうど良いのか,最良点を探すことにしよう.
式を立ててグラフを描けば一目瞭然だが,微分を知っていればグラフを描かなくても,グラフの極大点を割り出すことができる.どちらが好みだろうか?とりあえず,グラフを描くためにも式を求めることは必要なので,そこからやってみよう.
信号電圧がだとすると,回路を流れる電流は
であり,それにより,負荷
の両端の電圧
は
となるから,そこで消費される電力は
によって求められて,
となる.
や
が固定された条件で,
がどれくらいの時,一番大きな電力が消費されるかを考えたいので,縦軸を電力
,横軸を
にしたグラフを描くことになる.
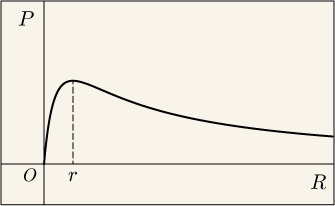
これが最大になる点は微分して 0 になるところである.つまり,
が 0 になるところだから,
のときが最大だということが分かる.つまり,出力インピーダンスと入力インピーダンスとが等しくなっている時に,もっとも多くの電力を次の段に伝えられるのである.このような目的で出力側と入力側のインピーダンスを合わせる設計にすることを「インピーダンス整合」あるいは「インピーダンス・マッチング」と呼ぶ.
グラフで分かるように,負荷抵抗が
よりも小さくなると急激に電力の伝達効率が落ちるので,量産の際には部品のバラつきを考慮して負荷抵抗
の側が少し大きめになるように調整しておいた方が問題が起きにくいかも知れない.
回路のマッチングが取れているとき,すなわちピッタリのとき,
での消費電力と
での消費電力は等しい.例えば,スピーカーを鳴らすためのアンプ(増幅器)と,スピーカー本体を例にして考えると,
スピーカーが音や熱として消費したのと同じエネルギーを,アンプの内部でも熱として無駄に消費することになる.50 W の出力のスピーカーなら,同時にアンプの内部でも 50 W を消費しており,合計 100 W を消費していることになる.これは避けられない.大きな出力を持つアンプに巨大な放熱板が取り付けられているのはそういう理由だ.(実際のスピーカーシステムはこれほど単純な構造ではないので成り立たないという指摘がありました)
特性インピーダンス
インピーダンスマッチングが重要になる別の場面がある.高周波の信号を長距離の電線で繋いで伝える場合だ.アンテナで捕まえた電波の信号を長いアンテナ線を通して引っ張ってきて装置に引き込む場合に,このようなことが重要になる.この時,インピーダンスが合っていないと接続部分で反射が起こって装置内に引き込めないという現象が起きる.
信号を受信する場合だけではない.送信時にも同様のことが起こる.電波を送信するためにケーブルを介して信号をアンテナに送るのだが,効率よく送信されず,信号が戻ってきてしまったりして送信機に大きな負担がかかったりするのである.出て行くはずの電力が出て行かずに戻るので,過剰な発熱を起こしたりする.
これは極めて高周波の信号を扱う時だけに関係する話であり,音声信号のような低周波ではほとんど気にしなくて良い.にもかかわらず心配してこだわる人を割りと良く見かけるので,ちょっと情報不足のせいで混乱してしまっているのだろう.
周波数が低い交流の場合には一本の電線の端から端までほとんど同じ電圧だと考えていれば良い.しかし周波数が高くなってくると,同じ一本の電線上でも場所によって電圧が違ってきてしまうことになる.まずはそれがなぜなのかを説明しよう.
電線の中を電圧の変化が伝わるのは,物質中を伝わる電磁波と同じことである.それは大体光の速さと同じくらいだと考えていい.真空中の光速よりは数十パーセントほど遅いくらいである.例えば 300 MHz くらいの電磁波だと,その波長は 1 m くらいになる.それくらいの信号を電線を使って伝えようとすると,25 cm もあれば 0 から最大まで変化するのである.このように,どれくらいの電線を長距離と呼ぶのかは周波数によって違ってくるわけだ.
音声信号の周波数は 10 kHz 程度であって,電線中での波長は 30 km ほどである.それほどまでに長いケーブルを使うような場合にだけ気にすればいい話だということになる.例えば,昔のアナログ方式の電話線などがそうだ.しかしそれほど線が長いと,むしろ電線自体の抵抗による電力の損失の方が気にすべき問題になる.末端の負荷抵抗をそれなりに大きくしておかないと,電線に掛かる電圧の方が大きくなって,肝心の末端のスピーカーにはちっとも電圧が掛からず,信号がうまく伝わらないのである.
このことによってなぜ信号の反射が起こるのかというのを説明するのは少し難しくなるので,別のもっと理論重視の記事で詳しく話そう.
ごくごく簡単に説明すると,電線が持つ「特性インピーダンス」という量とアンプの持つインピーダンスが一致していないといけないのである.この特性インピーダンスというのは,電線の長さに比例するわけではない.電線の構造によって決まるものであって,電線が長くても短くてもその大きさは変わらないという不思議な概念だ.特に,ケーブルの抵抗成分や漏れ電流が小さな場合には信号の周波数にも関係ない値になる.
このようにちょっと変わった概念であるが,電線を伝わる交流の電圧と電流の比を意味しており,単位は Ω(オーム)で表されるような量なのである.この辺りの話は無線工学をやると重要になってくる.
予告など
このように,色んな場面で複数の理由でインピーダンスマッチングが重要になっている.必要以上にこだわる人もよく見かけるのだが,それほどこだわる必要のない場面も多い.そこは理論的に正しく見極めよう.
さて,インピーダンスマッチングが大事だと言われても,一体どのように両者を合わせたらいいだろうか?調整する手段は幾つかある.トランジスタ回路を使う場合もあるし,トランスを使う場合もある.それはまた後ほど徐々に説明することにしよう.
オーディオ関連の趣味を持つ人たちの間で,特にスピーカーの性能にからんでインピーダンス・マッチングの話が良く出るので,特別にその辺りを説明する記事も書くことにしよう.










