力のモーメント
前回の話から,中心から離れているほど物体を回転させるのに効率が良いという事が分かる.しかし「効率が良い」とはあいまいな表現だ.何かしっかりとした定義が欲しい.この「物体を回転させようとする力」の影響力をうまく表すためには回転の中心からの距離とその点にかかる回転させようとする力
を掛け合わせた量
を作れば良さそうだ.これは前の話から察しがつく.
この
は「力のモーメント」と呼ばれている.正式にはベクトルを使った少し面倒な定義があるのだが,しばらくは本質だけを説明したいのでベクトルを使わないで進むことにする.しかし力の方向についてはここで少し注意を入れておかないといけない.
先ほどから私は「回転させようとする力」という表現をわざわざ使っている.これには意味がある.力がおかしな方向に向けられていると,それは回転の役に立たず無駄になる.それを計算に入れるべきではない.次の図を見てもらいたい.
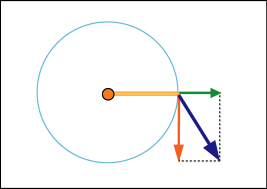
青い矢印で描いた力は棒の先についた物体を回転させるだろうが無駄も多い.この力を 2 方向に分解してやると赤と緑の矢印になる.赤い矢印の力は物体を回転させるが,緑の矢印は全く回転の役に立っていない.つまり,上の定義式でのとしては,この赤い矢印の大きさだけを代入すべきなのだ.「回転させようとする力」と言ってきたのはこういう意味だったのである.
力のモーメントをこのように定義すると,物体の回転への影響を表しやすくなる.例えば中心からの距離が違う幾つかの点にそれぞれ値の違う力がかかっていたとして,それらが互いに打ち消す方向に働いていたとしよう.ベクトルを使って定義していないのでどちら向きの回転をプラスとすべきかははっきり決められないのだが,まぁ,適当にどちらかをプラス,どちらかをマイナスと自分で決めて
を計算してほしい.それが全体として 0 になるようなことがあれば,物体は回転を始めないということになる.また合計の
の数値が大きいほど,勢いよく物体を回転させられるということも分かる.
は,物体の各点に働くそれぞれの力が,物体の回転の駆動に貢献する度合いを表した数値として使えることになる.
モーメントとは何か
この「力のモーメント」という言葉の由来がどうも謎だ.モーメントとは一体どんな意味なのだろうか.
運動量は英語で「モーメンタム(momentum)」と呼ばれるが,この「モーメント(moment)」とはとても似ている言葉である.学生時代にニュートンの「プリンキピア」(もちろん邦訳)を読んだことがあるが,その中で,ニュートンがおそるおそるこの「運動量(momentum)」という単語を慎重に使い始めていたことが記憶に残っている.この言葉はこの時代に造られたのだろうということくらいは推測していたが,語源ともなると考えたこともなかった.
どういう過程でこの二つの単語が使われるようになったのだろう?まず語尾の感じから言って,ラテン語系の名詞の複数形,単数形の違いを思い出す.data は datum の複数形であるという例は高校でよく出てきた.なるほど,ラテン語から来ている言葉に違いない,と思って調べると,「moment」はラテン語で「動き」を意味する言葉だと英和辞典にしっかり載っていた.「時間の動き」→「瞬間」という具合に意味が変化していったらしい.このあたりの発想の転換は理解に苦しむが・・・. しかし,運動量の複数形は「momenta」だということだ.今知りたい「モーメント」とは直接関係なさそうだ.
他にどこを調べても載っていない.回転させる時の「動かしやすさ」というのが由来だろうか.私が今までこの言葉を使ってきた限りでは,「回転のしやすさ」「回転の勢い」というイメージが強く結びついている.
角運動量
力のモーメントの値が大きいほど,物体を勢いよく回せるとのことだった.ところで・・・回転の勢いとは何だろうか.これもまたあいまいな表現であり,ちゃんとした定義が必要だ.そこで「力のモーメント」と同じような発想で,回転の勢いを表す新しい量を作ってやろう.ある半径で回転運動をしている質点の運動量
と,その回転の半径
とを掛け合わせるのである.
「力のモーメント」という命名の流儀に従うなら,これを「運動量のモーメント」と呼びたいところである.しかしこれを英語で言おうとすると「moment of momentum」となって同じような単語が並ぶので大変ややこしい.そこで「angular momentum」という別名を付けたのであろう.それは日本語では「角運動量」と訳されている.
なぜこれが回転の勢いを表すのに相応しいのだろうか.例としてある点の周りを棒に繋がれて回っている質点について二通りの状況を考えよう.両方とも質量,運動量は同じだとする.ただ一つの違いは中心からの距離だけである.一方は,中心から遠いところを回っており,もう一方は中心に近いところを回っている.前者は角運動量が大きく,後者は小さい.回転の半径が大きいというだけで回転の勢いが強いと言えるだろうか.
質点に直接さわって止めようとすれば,中心に近いところを回っているものだろうと,離れたところを回っているものだろうと労力は変わらないだろう.運動量は同じであり,この場合,速度さえも同じだからである.勢いに違いはないように思える.それだけではない.中心に近いところで回転する方が単位時間に移動する角度は大きい.回転数が速いということだ.むしろ角運動量の小さい方が勢いがあるようにさえ見えるではないか.
角運動量の解釈を「回転の勢い」という言葉で表現すること自体が間違っているのかもしれない.力のモーメントも角運動量
も元はと言えば,力
や運動量
にそれぞれ回転半径
をかけただけのものであるので,力
と運動量
の間にある関係式
と同様の関係式が成り立っている.
つまり角運動量とは力のモーメントによる回転の効果を時間的に積算したものである,と言う以外には正しく表しようのないもので,日常用語でぴったりくる言葉はないかも知れない.回転半径の長いところにある物体をある運動量にまで加速するには,短い半径にあるものを同じ運動量にするよりも,より大きなモーメント
あるいはより長い時間が必要だということが表れている量である.
もし上の式で力のモーメントが 0 だったとしたら・・・,つまり回転させようとする外力が存在しなければ,
であり,
は時間的に変化せず一定だということになる.これが「角運動量保存則」である.もちろんこれは,回転半径
が固定されているという仮定をした場合の簡略化した考え方であるから,質点がもっと自由に動く場合には当てはまらない.実は質点が半径を変化させながら運動する場合であっても,
が 0 ならば角運動量が保存することが言えるのだが,それはもう少し後の方で説明することにしよう.この後しばらくの話では回転半径
は固定しているものとして考えていても差し支えないし,その方が分かりやすいだろう.
角速度、角加速度
力や運動量を回転に合わせて拡張した概念が出てきたので,速度や加速度や質量を拡張した概念も作ってやりたいところである.
しかし,今までと同じ方法を使って何も考えずに単に半径をかけたのではよく分からない量が出来てしまうだけだ.そんな事をしなくても例えば,回転の速度というのは単位時間あたりに回転する角度を考えるのが一番分かりやすい.これを「角速度」と呼ぶ.回転角をで表す時,角速度
は次のように表現される.
さらに,角速度がどれくらい変化するかという量として「角加速度」という量を定義する.角速度をもう一度時間で微分すればいい.この辺りは何も難しいことのない概念であろう.
大学生がよくつまづくのは,この後に出てくる,質量に相当する概念「慣性モーメント」の話が出始める頃からである.定義式だけをしげしげと眺めて慣性モーメントとは何かと考えても混乱が始まるだけである.また,「力のモーメント」と「慣性モーメント」と名前が似ているので頭の中がこんがらかっている人も時々見かける.しかし,そんなに難しい話ではない.
慣性モーメント
運動量に相当する「角運動量」と速度に相当する「角速度
」が定義できたので,これらの関係を運動量の定義式
と同じように
という形で表せないか,と考えてみよう.この「回転に対する質量」を表す量
を「慣性モーメント」と呼ぶ.本当は「力のモーメント」と同じように「質量のモーメント」と名付けたかったのかも知れない.しかし今までと定義の仕方のニュアンスが違うので「慣性のモーメント(moment of inertia)」と呼ぶことにしたのであろう.日本語では「of」を略して「慣性モーメント」と訳している.
質量が力を加えられた時の「動きにくさ」や「止まりにくさ」を表すのと同様,この「慣性モーメント」は力のモーメントが加わった時の「回転の始まりにくさ」や「回転の止まりにくさ」を表しているのである.
では,慣性モーメントをどのように定義したらいいだろうか?角運動量は「半径×運動量」であり,運動量は「質量×速度」であって,速度は「角速度×半径」で表せる.これは口で言うより式で表した方が分かりやすい.
これと一つ前の式とを比べると慣性モーメント
は
と表せば良いことが分かるだろう.これが慣性モーメントが定義された経緯である.この定義式ばかりを眺めて,どういう意味合いで半径の 2 乗が関係しているのだろうかなんて事をいくら悩んでも無駄なのである.










