てこの原理
我々はシーソーや天秤はかりなどで,支点から離れたところに力をかけるほど物体を回転させるのに有利になることを知っている.また,二人でバットの回し合いをするときにバットの太いところを握る方が細いところを握るより有利になるのは同じ原理である.ドライバーの柄の部分が太くなっているのはこれを応用したものである.
このように,回そうとする中心点(それは支点と呼ばれることもあるが)からの半径が大きいほど,効率よく物体を回転させることが出来るのである.
我々はこれらのことをよく「てこの原理によって・・・」と一言で片付けているが,よくよく考えるとなぜこのような事が起きるのであろうか?「原理」と呼ばれているが,本当に原理と呼ぶほど基本的な法則なのだろうか?いや,そうではない.もっと基本的なことから説明がつくのである.
てこの原理が成り立つ理由
一本の棒で結ばれた二つの質点を考える.そしてこの棒の端に近い点を支点として,そこを中心に回転させることにする.
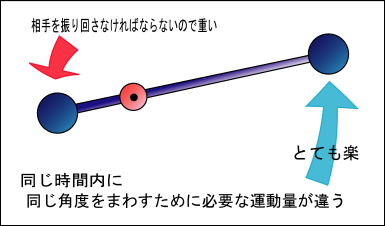
この棒を回転させるときに,我々は回転半径の小さい方に繋がれた質点を押す方がより重く感じることを日常感覚として知っている.しかし,それはなぜだか理解しているだろうか?それは,半径の小さな方の質点を押してこの棒を回すとき,我々は棒の反対側に繋がれた質点をも動かさなければならないからである.反対側の質点は回転半径が大きい分,同じ角度を回すときにより大きな運動量が必要なのである.単位時間に与えられる運動量の大きさを「力」と呼ぶことは以前に説明した.単位時間に,より大きな運動量を与えてやらなければこの棒は回せないのである.
これで,回転半径が小さいほどより大きな力が必要な理由が説明できたであろう.別に,てこの原理がこの宇宙の絶対法則というわけでもないのだ.ただ「2 点の間を結ぶ棒」という制約条件が入る事によって当然成り立つ現象なのである.
二つの点が結ばれているという条件は大切である.もし棒がついていなければ,もう一方は回転半径など気にすることなく苦もなく直進することになる.回転というのは 2 つ以上の物体が「結ばれている」という条件によって大きな意味を持ち始めるのである.そしてこの世にある物質は「力」という制約条件によってお互いに結ばれているのである.










