素粒子論：ニュートリノ振動

3 種のニュートリノ

ニュートリノは 3 種類あり,「電子ニュートリノ」「（ミュー）ニュートリノ」「（タウ）ニュートリノ」と呼ばれている.これらの呼び名の由来は,電子と同じ「第 1 世代」に属するニュートリノ,ミュー粒子（ミューオン）と同じ「第 2 世代」に属するニュートリノ,タウ粒子（タウオン）と同じ「第 3 世代」に属するニュートリノという意味である.それぞれを ν_e , ν_μ , ν_τ という記号で表すことにする.

3 種のニュートリノは質量の違い以外はほとんど同じ性質を持っていると考えられている.これは,電子とミュー粒子とタウ粒子が質量に違いがある以外はほとんど同じ性質を持っていることからも強く類推される.

しかしニュートリノの質量は極めて小さいらしく,直接の測定はいまだできていない.ニュートリノの質量はひょっとするとどれも 0 であるかも知れないと長い間思われていたが,そうではないという証拠が最近になって見付かったのだった.それが「ニュートリノ振動」と呼ばれる現象である.

ある種のニュートリノが核反応で発生してから長い距離を移動する間に,別種のニュートリノに変化したり再び元に戻ったりを繰り返すのである.この変化を繰り返す様子を「振動」と呼んでいるのであって,ニュートリノ自体が空間を揺れながら進むとかいうわけではない.これはニュートリノの種類によって質量が違っていなければ説明できない現象である.

今回はその理論を説明しよう.

ニュートリノ混合

ニュートリノには 3 つの種類があると言ったが,我々が素粒子の反応を通して観測しているこれらの粒子は理論的に純粋な状態ではなく,それぞれが微妙に重ね合わさったものではないかという仮説が立てられた.これはクォーク理論からの類推である.

理論的に純粋な 3 つのエネルギーの固有状態 $|ν_{1}>}$ , $|ν_{2}>}$ , $|ν_{3}>}$ があったとする.それぞれは次のような固有状態になっているということである. そして,例えば我々が電子ニュートリノ |ν_e>} だと思って観測している粒子は,実はこれらの状態が重ね合わさって次のようになっていると考えるわけだ. この時の係数 a,b,c はどうなっているのだろうか.話を簡単にするため「第 2 世代」まで,つまり電子ニュートリノとミューニュートリノの二つに絞って考えよう.状態も二つだけを使って,次のようになっているとしてみる. このイメージは分かりやすい.もともと直交する二つの状態があって,2 次元の内部自由度を持っているわけだが,何らかの理由でこれらがある固定角度だけずれた状態の粒子が,「核反応に関与するニュートリノ」として実現しているというわけだ.

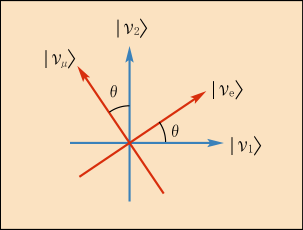
2種類の理論的なニュートリノの状態がある角度で混じり合って現実の2種類のニュートリノが実現していることを表す図

このは現実の 3 次元空間での角度とは何の関係もない.抽象的な内部空間での状態の混じり合い方が,あたかも回転のように表せると言っているのである.この回転的なズレの角度は時間によって変化したりはしないものである.

このイメージは元々クォークに対して提案されたもので,当時はまだストレンジクォークまでしか見付かってなかったので,上の式と同じように第 2 世代までしか考える必要がなかった.クォークの場合,この角度のことを「カビボ角」と呼ぶ.やがてクォークも 3 世代まで見付かって,それぞれの世代が互いに回転的にずれているので,3 次行列で表されるような複雑な混合を考える必要が出て来た.それが「カビボ・小林・益川行列」,頭文字を取って「CKM行列」である.これはクォークが世代の異なる別種のクォークへと変化を起こす理由を説明している.

ニュートリノに対しても同じ考えを当てはめているわけだが,その場合には「カビボ角」という用語は使わない.「ニュートリノ混合角」と呼んでいる.カビボ角は約 13°であることが分かっているが,ニュートリノの場合の混合角はそれとは値が違っており,例えば ν_e と ν_μ の混合角 $θ_{12}$ は約 34°だそうだ. ν_μ と ν_τ の混合角 $θ_{23}$ は理論上の最大値である 45°近くだが,まだ正確には分かっていない.しかし ν_e と ν_τ の混合角 $θ_{13}$ は極めて小さく,0 ではないかと考えられていたこともあったくらいだが,そうでもないらしい.このような角度の生じる理由はまだよく分かっていない.

確率計算

$|ν_{1}>}$ はエネルギー $E_{1}$ の固有状態, $|ν_{2}>}$ はエネルギー $E_{2}$ の固有状態なので,位相はそれぞれ $e^{iE_{1}t/ℏ}$ , $e^{iE_{2}t/ℏ}$ のように変化する.つまり,ミューニュートリノとして生じた |ν_μ>} という状態は時間経過と共に次のように変化する. これはもはやミューニュートリノとは呼べない状態にまで変化したりするので敢えての文字を入れずに |ν(t)>} のように書いておいた.この中に電子ニュートリノ的な成分がどれだけ含まれるのかを計算してみよう.つまり,と |ν_e>} の内積を計算してやればいい. $<ν_{1}|ν_{1}>=<ν_{2}|ν_{2}>=1$ , $<ν_{1}|ν_{2}>=<ν_{2}|ν_{1}>=0$ という関係を使えば良いだけなので簡単だ. 確率を計算するのだったら,これの絶対値の 2 乗を計算してやる必要がある. $e^{-iE_1 t/ℏ}$ の部分の絶対値は 1 だから消せてしまうし,もっと簡単になりそうだ. つまりこれが,元々ミューニュートリノだったものが,時間の経過に応じて電子ニュートリノとして観測される確率である.

波長を求める

ここでエネルギー差 E_2 -E_1 について考えてみよう.これは質量差のことではなく,粒子が持つ全エネルギーの差を意味している.運動量で運動する粒子の全エネルギーは相対論によって次のように表されるのだった. 単独で相互作用せずに運動する粒子は運動量保存則があるのでこの式でのの値は固定である.今回の設定で変化するのは質量の方である.ニュートリノの質量は極めて小さく,質量エネルギーよりも運動エネルギーの方がはるかに大きいことを利用してテイラー近似してみよう. これを使えば, だということになる.ほとんど E=pc が成り立っていることを使えば,式からを消してやることもできる. Δ[(mc^2)^2] は「質量エネルギーの 2 乗の差」という意味で導入した.はニュートリノの全エネルギーである.これを先ほどの確率の式に代入すると次のようになる. ニュートリノはほぼ光速で進むので,秒間に L=ct だけ進む.つまり, t=L/c である. つまり,飛行距離に応じて電子ニュートリノとして観測される確率が上がったり,ミューニュートリノとして観測される確率が上がったりを繰り返すことが言えるのである.その変化の波長を求めたければ, と置くことで, だと分かる.つまり,ニュートリノの発生源からの距離を様々に変えてニュートリノの検出確率を測定し,同時にそのエネルギーを測定することで,ニュートリノの種類による質量差がどれくらいであるかを見積もることができるのである.

原子炉から出ているニュートリノを数百メートルや数百キロメートル離れた場所で測定してみたり,地球上層大気に当たった宇宙線との核反応で生じたニュートリノを地球の裏側で測定してみたり,太陽の内部で発生しているニュートリノを測定してみたりといった努力が続けられている.

あれれ？

ところで,この計算に使った質量というのは状態 $|ν_{1}>}$ と $|ν_{2}>}$ の質量のことだから,正確には電子ニュートリノとミューニュートリノの質量差のことではないようだ.電子ニュートリノやミューニュートリノというのはそれらの状態の混合だというのなら,電子ニュートリノやミューニュートリノの質量というのはどう表してやればいいのだろう？

どうやら,核反応で出てきた直後のニュートリノは質量が確定していない状態であると言って良さそうだ.つまり,異なる質量を持つ複数の可能性が重ね合わさった状態だということになる.だから「それらの粒子にははっきりした質量はない」というのが答えだろう.

だとしたらクォークの質量についても同じことが言えるのだろうか.そう言えばずっと昔に読んだ何かの本では,クォークの質量について,ごまかすような表現が使われていた気がする.当時はまだ当てずっぽうの値しか載っていなかったが,「クォークの質量は普通に想像する意味での質量とは意味が異なるからあまり気にしなくていい」というような感じだった.これはクォークの混合について言おうとしていたのだろうか.そもそもクォークは単離できない粒子なのだから正確な数値にあまり意味はないのかも知れない.3 つのクォークが集まって出来ているハドロンの質量はクォークの質量を合計しても全く足りなくて,内部の運動エネルギーがハドロンの質量の大半を占めるのだった.

しかし,電子やミューオンやタウオンについてはかなりはっきりした質量が明らかになっている.それらはどういう意味での質量なのだろう,と思って調べてみると,どうやらこれらの粒子には今のところ混合が起きている証拠は見付かっていないのだそうだ.