物理数学：コーシーの積分定理

一周すると 0 になる？

複素積分の値は積分路の選び方によって変わるという説明をした.前回の具体例ではいかにもそうなっているように見せかけておいた.ところが f(z)=z や f(z)=z^2 などの簡単な関数で試してみると,始点と終点さえ固定しておけば,どんな積分路を選んでも結果が変わらないという事実に気が付く.

もし積分の値が始点と終点だけで決まるとすると,次のことが言えるはずだ.まず,始点から終点に向かう二通りのコースを考えてみる.

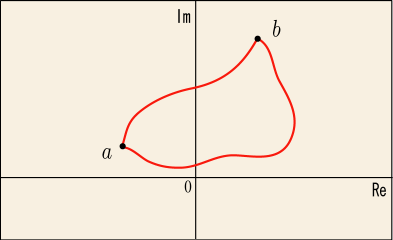
一方のコースでからに向かい,別のコースでからに戻ってくるとどうなるだろうか？同じコースを逆にたどりながら積分する時には,元の計算結果と符号が逆転した結果が得られるのだった.今はどちらのコースを通っても同じ値になるというのだから,どこかへ行って,別のコースで戻ってきた場合の積分の合計値はちょうど打ち消し合って必ず 0 になる.つまり,どんなコースでもいいから輪を描くように一周してくるコースの積分はいつでも 0 になるはずだ. 輪を描いて一周してくる積分を表すのに $\oint$ という記号を使うことがある.今後も時々使うつもりでいるので覚えておいてほしい.

さて,どんな関数のときにこのような性質が成り立っていると言えるのだろう？

秘密にしていても話が進まないから答を言ってしまおう.この積分路の輪の内部で関数が正則であるときには必ず成り立つのである.これを「コーシーの積分定理」と呼ぶ.

例えば f(z)=1/z を考えると,この関数は z=0 の点では定義できないので正則ではない.だから原点を囲むようなコースを選んで計算すると 0 にはならない.しかしそれ以外の点では正則であるから,原点を囲まないように回るならばちゃんとこの定理によって 0 になる.

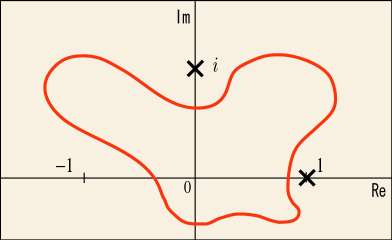
例えば f(z)=1/(z-1)(z-i) という関数ならば,気を付けないといけないのは z=1 の点と z=i の点である.この 2 つの点を含まないように一周する限りはどんなコースを取ってもちゃんと 0 になる.

関数が正則であるというのは複素微分ができるかどうかというものだった.その微分に関する性質が,このような積分の場面で効いてくるというのは一体どういう理屈なのだろうか？

なぜ成り立つのかのイメージ

数学の教科書ではこのコーシーの積分定理の証明のためだけにかなりのページを費やしているものが多い.きちんと説明しようとすればそれなりのページ数が必要になるのだ.本当に知りたい人にはそういうものを読んでもらえばいいので,ここでは「なるほど,いかにも成り立っていそうだ」と納得できるくらいの簡単な説明で終わらせることにしよう.

まず,ほぼ一点と呼べるくらいのごく狭い範囲で一周して積分することを考えてみよう.変数の変化を表すはその小さな積分路に沿って次々と方向を変えることだろう.をちょっと大きめの矢印でイメージすると,その矢印の方向はぐるりと一周するわけだ.今はとても狭い積分範囲を考えているので,ほとんどその場で一回転するようなものである.

ここで,もし積分しようとしている関数 f(z) が一定値だったらどうなるかを考えてみよう.それは回転するを少しずつ足し合わせたものに,最後に一定値である f(z) を掛けるのと同じである.一周分のを合計すると結局は元の場所に戻るのだから,この答は 0 である.しかしまだ「コーシーの積分定理」の内容には程遠い.実際には f(z) は一定値なんかではなく,場所によって値が変化しているからだ.どんな変化をしていると言えるのだったか,そこが重要だ.

正則な複素関数というのは微分可能だという意味だった.微分可能というのは,変数が複素平面上のある一点からどの方向へ向かっても,関数の値の変化率 f'(z) が同じ複素数値になっているということだった.つまり,次の関係が成り立っている. ここで,複素数の積の図形的意味を思い出してもらいたい.互いの絶対値どうしは掛け合わされ,偏角どうしは足し合わされるのだった. f'(z) にに掛けるというのは,の絶対値を f'(z) に掛けて,の方向と同じだけ f'(z) を回すことに相当するわけだ.つまり,ある 1 点を中心にしてそこから一定距離だけ離れた円周上を見回すと,関数 f(z) の変化量 df(z) の絶対値はどこを向いてもほぼ同じであるし,その偏角はまるで,見回す角度と連動しているかのように,ぐるりと一周しているのである.

さて,このような変化量を小さな円周上で積分したらどうなるだろうか？回転する量にさらにを掛けながら足してゆくわけだから丸 2 周分の変化をすることになるわけだが,その合計は結局全て打ち消し合って 0 になる！

関数が変化しない場合には 1 周積分は 0.変化分だけを別に 1 周積分しても 0.結局,正則関数を微小領域で一周積分したものは 0 になるというイメージはだいたいこんなものだ.

以上の話は割りときれいな円形の積分路をイメージしているものだが,少々コースから外れて半径が大きめのところに踏み込んだとしてもいつか戻ってこなくてはならないし,結局 1 周分の角度を回らなくてはならないことに変わりはないので,少々コースがいびつでも同じような結果になるだろうという感じになっている.厳密なことは別の教科書に任せよう.

これをどんな形の積分路でも成り立つというイメージに繋げないといけない.その為には次の図のようなことを考えるのである.

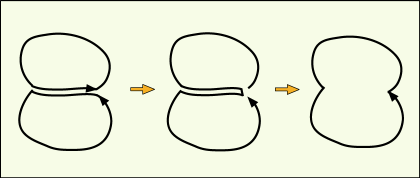
二つの微小領域の 1 周積分はどちらも 0 である.だから,二つの積分路を繋いで一方の領域を回ってから,もう一方を回るようにしても積分値は 0 である.この二つの領域の境界線での積分は同じ所を往復しているだけだから,省いても構わない.つまり,二つの領域をつないだ領域の外側を回るコースでの積分も 0 であることが言える.

このようにして多数の微小領域を繋いで行けば,任意の形の積分路を作っても全体の積分値は 0 だと言えるのである.

グリーンの定理を使った説明（おまけ）

もし読者がグリーンの定理というものを知っていれば,証明はずっと簡単になる.グリーンの定理というのは平面上の線積分を面積分に書き換えたり,その逆をしたりするのに使われるもので,次のように表される. 見ての通り,複素関数とは関係のない定理だ.知らなければ仕方がない.いつか知ることもあるだろう.今はこんなやり方もあるのだという程度に理解しておいてもらえればいい.

複素関数 f(z) の変数を z=x+iy で表すと,複素関数の方は実部と虚部に分けてと表すことが出来る.これを使って複素積分を変形してやると, となる.すでに変形過程でグリーンの定理を使わせてもらった.この最後の積分の中身を見ると,正則な関数の条件である「コーシー・リーマンの関係式」を思い出す.それは次のようなものだった. これを当てはめるとどちらの積分も 0 になることが分かる.要するに,周回積分の領域内で常に正則であるなら,その積分の値は常に 0 であるということが言えるのである.

不定積分が使える？

こうして「積分の値が始点と終点だけで決まってしまうことがある」ことをコーシーの積分定理で説明できるようになった.始点と終点だけで積分値が決まってしまうような場合には途中の経路なんてものはもう関係ないのだから,わざわざ経路に沿った積分をしなくても答が出せるような何らかの法則が見い出せるのではないだろうか？

実はとても楽チンな方法がある.ただし「関数が複素平面の全域で正則である場合」に限り使用可能だ.

次のように,始点の複素数値と終点の複素数値だけで積分値を決められるような関数 F(z) が存在しているのである. この F(z) と f(z) は次のような関係になっている. それって,つまり, F(z) は f(z) の原始関数であって,やっぱり,実数の積分の時の不定積分のようなルールが成り立っているということ！？前回は使っちゃダメだって言ったじゃないか！

そう,これは気を付けて使わないとダメなのだ.だからいつでも使えるような印象を最初に与えてしまうわけには行かなかった.本当のことを言うと「関数 f(z) が複素平面の全域で正則」でない場合にもこの法則が使える場合があるのだが,まだこの段階では使用を制限しておくことにしよう.

この法則が使える理由を証明するのは簡単だ.前回の基本的な計算のやり方を思い出してもらいたい.積分経路を z(t) で表して,始点と終点を z(0)=a , z(1)=b となるように決めておこう.また,式の解釈が楽になるように G(t)≡F(z(t)) という関数を定義しておこう. ハイ！これで終わりだ.

しかしこの説明を見る限り,関数が複素平面の全域で正則でなくても,いつでも使えそうではないか？積分経路が「正則でない点」を踏みさえしなければ成り立つ気がする.一体,何を恐れて使用に制限を付けているのだろう？

なぜ使用を制限するのか

この方法を使われると困った結果になる典型例は f(z)=1/z の場合だ.この関数は z=0 の 1 点で定義されていないから,なるほど確かに「全域で正則」にはなっていない.

z=0 を内部に含むような円形コースではコーシーの積分定理も使えないのだった.実際にやってみると分かるが,始点と終点を固定しておいても, z=0 の点の向こうを回るコースとこっちを回るコースとでは値が違っていることが確認できる.

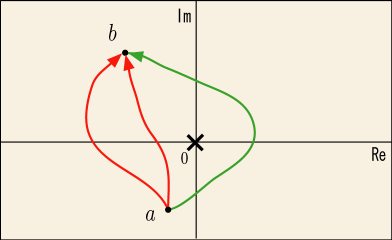
ところが,今しがた紹介した「不定積分の方法」は始点と終点だけで積分値が一つに決まると主張しているのだから,確かに実際と比べて矛盾がありそうだ.なぜこんなことが起きるのであろうか？

f(z)=1/z の原始関数は F(z)=log_e z であった.そう言えば,我々はまだ log 関数の複素平面上での性質を調べていないのだった.ちょっと面倒かも知れないが調査に付き合ってもらえるだろうか？

対数関数の性質

実数で定義されていた色んな関数をテイラー展開したものを複素平面にまで拡張して使用しようというのが,ここまで取って来た方針であった.しかし log_e x を x=0 の周りでテイラー展開しようとしても, 1/x のに 0 を代入するわけには行かないので実行不可能である.かと言って x=1 の周りで展開しても (x-1),(x-1)^2, (x-1)^3, … のような項が続くことになるのであり,見栄えの良いものではない.そこで,関数の形を少し変えて f(x)=log_e(1+x) としたものを x=0 の周りにテイラー展開することが良く行われる. 複素数に拡張しても問題なく使えそうだ.ただしこの級数の収束半径は 1 だから,複素平面上の限られた範囲内でしか使用できない.それは少し面倒ではあるものの大きな問題ではないだろう.別の点を中心にしてテイラー展開してやればいいわけだ.

とは言うものの,今回のようなことを考えるにはさっきの形では使いにくいな.普通に x=1 の周りで展開してみよう. 特に問題なし. x=2 の周りで展開するとどうなるだろう？あまり見かけたことのない形だ.これでは規則性が分かりにくいな.具体的な数値にせず, x=a の周りで展開したらどうなるか,というのを考えてみよう. 収束半径を計算してやると,になるんだな. テイラー展開の中心を右へずらすほど収束半径がどんどん広がって使える範囲が広がるのは有難いのだが,こんなことを幾ら考えてみても,複素平面の左側にまでは拡張できそうにない.

そこで,全く別の考え方に頼ることにしよう.そもそも対数関数というのは指数関数の逆関数として定義されたものだったではないか. なぜこんな基本的なことを後回しにしていたのか,と言いたいくらいだ.

もちろん,いきなりこの考えに飛びつくと読者の不信を招きそうだったからである.

複素平面にまで拡張した指数関数がどんなものだったか復習をしてみよう.複素数に対してを対応させる関数としての指数関数を考える. 考えやすくなるなるように, z=a+bi （もも実数）とすると, であり,の絶対値を決めているのは e^a であり,（ $e^{bi}$ の絶対値は 1 だったことを思い出そう！）偏角を決めているのは $e^{bi}$ の方である.の実数部分が増加するほどの絶対値は e^a のように増加する. e^a は決して 0 以下にはならないから, e^a はの絶対値そのものを表していると言えるだろう.そしての虚数部分であるはの偏角そのものであり,が増加するほどは複素平面上をぐるぐる回る.何度でも回る.の値が増えるたびに,は何度でも同じ値を取ることになる.

以上がとの関係であり,この対応を逆にしたのが複素平面上での対数関数である. つまり,としてある 1 点を決めたら,それに対応するは幾つでもあるのであり,ある値が当てはまったとしたらそれに 2πi だけ足した値も,さらに 2πi 足した値も,皆当てはまる.普通は関数といえば一つの変数の値に対して一つの値を返すものである.これを「1 価の関数」と呼ぶ.それに対して複数の値を返すような関数は「多価関数」と呼ばれる.ところが「複素平面に拡張した対数関数」は二つや三つどころではなくて,一つの変数の値に対して無限個の値を返すのである.このような性質を「無限多価性」と呼ぶ.

e^a が決して 0 にならないので, w=0 に対応する値はない.しかしそれ以外の全ての点で log_e w は値を持つ.例えば,実数の対数関数では決して考えることができなかった log_e (-1) というものも,ちゃんと対応する値を持つ. w=-1 になるには a=0 で b=π であればいいのだから, z=πi だ.そして先ほど話した無限多価性があるので,それに 2πi を足したり引いたりしたものも当てはまる. 実数の範囲だけで対数を考えていた時にはこの無限多価性に気付かずにいたのだ.もちろん実数の範囲であっても同じことが成り立ち,例えばこれまでは log_e 1=0 だと考えていたわけだが,本当はのようになっている.先ほどのテイラー展開では,まるで値が一つに定まるかのように表されていて無限多価性が出てきていないが,これはテイラー展開に問題があったわけではない. log_e a と書いた部分が無限多価性を持つと考えればいい.例えば x=1 の周りの展開では単に log_e 1=0 だと考えて省略してしまっているが, log_e 1=2nπi だとして右辺に反映させてやれば解決である.

なぜ使用を制限するのか（つづき）

不定積分の方法を制限しておきたい理由が分かってもらえただろうか？ log_e z は原点を除く全ての点で値を持つことがはっきりしたのでその点についてはありがたい.それは問題ではないのだが,値が一つに定まらないという問題があるのだ.

先ほど,「 f(z)=1/z という関数を積分しようとすると, z=0 の点の向こうを回るコースとこっちを回るコースとでは値が違っていることが確認できる」という話をした.実際にどれだけ違っているかというと,いつでも 2πi だけ違っているのである.

もっと詳しいことを言うと,積分のコースとしては何度も同じ所をぐるぐると回っても良いわけで,z = 0 の点の周りを一周回るたびに積分値は 2πi だけ変化するのである.今の log の話と符合する話になっている.

では不定積分が対数関数になる f(z)=1/z の場合だけ使用を制限すればいいんじゃないかと思うかも知れないが,なかなか見かけでは判断できない場合があるのだ.まぁ,臭いものには蓋をしておけ,というわけだ.

まだ納得が行かないかも知れない.そんな人は,これから複素関数の性質をもっと深く知ることになると思うが,その上で自己責任で使用して欲しい.今見ているのは,全体からすれば,まだ個々の話に過ぎないのである.これからだんだんと一つの話にまとまってくる.

次回からは,正則でない点を含む関数の性質について調べて行く事にしよう.