物理数学：8 次元表現

先は長いのかも

前回は SU(3) の表現の例としてゲルマン行列を紹介した.ゲルマン行列は 3 次の表現であったが,他の次数による表現はどんなものがあるのだろうか.

少なくとも生成子の数と同じ 8 次元表現というものがあるはずである.それは構造定数から機械的に導き出すことができて,随伴表現と呼ばれるのだった.しかし 8 次の行列なら固有ベクトルも 8 つあるはずだ.それらはウェイト図の上にどのように並べることができるだろうか？この段階ではまだちょっと想像がつかない.

3 次と 8 次の他にはどんな表現が可能なのだろうか？あらゆる可能性を調べ上げてみたい.

ルート図

SO(3) や SU(2) のときの $L_{+}$ や $L_{-}$ と同じようにウェイトを上げ下げできる行列が作れるという話を前回少しだけしたのだった.具体的に見てみるのが一番早い. 6 つもあるので区別するための記号に苦労している. $L_{+}$ や $L_{-}$ の場合にはウェイトは一種類だけだったから上げるか下げるかだけで区別すれば良かったが,今回は 2 次元のウェイト図の上での移動を行わせる働きを持つものなので,移動する方向を,,というベクトルで表している.

最初の二つの式は $L_{+}$ や $L_{-}$ を作った時と全く同じ形をしている. λ_1 と λ_2 と λ_3 がパウリ行列と全く同じ構造なので,同じ結果になるのだろう. 右辺に 2 が出て来ているところが前と違っているが,本質的な差ではない.ゲルマン行列の全てを 1/2 倍すれば消すこともできるが,このままで行くことにする.この式の使い道はすでに分かっていると思うが,思い出すために書いておこう.最初の式は移項してと書けるが,この両辺を |m,s>} に掛けることで, となり, $λ_{+x}|m,s>}$ の λ_3 についての固有値は m+2 であることが分かるのである.つまり, $λ_{+x}$ はの値を 2 だけ大きなベクトルに変換する働きがあるというわけだ.今回はこれ以外に, λ_8 についても考えないといけないから,同じようなものを計算してやると, となる.これはあまり面白くないが,例えば最初の式は移項してとなるので,この両辺を |m,s>} に掛ければであり, $λ_{+x}|m,s>}$ は λ_8 の固有ベクトルではあるのだが,その固有値はのままであることが分かるのである.

結局 $λ_{+x}$ というのは |m,s>} を |m+2,s>} に変化させる働きがあると言えることになる.同じ理屈で $λ_{-x}$ というのは |m,s>} を |m-2,s>} に変化させる働きがあると言える.

次は $λ_{+y}$ について調べてみよう.これに関しては次のような関係があることが確かめられる. この結果を見ただけで分かると思うが, $λ_{+y}$ というのは |m,s>} を |m+1,s+√3 >} に変化させる働きがあることが導かれるだろう. $λ_{-y}$ については省略するがこれとは符号が逆になる.

最後に $λ_{+z}$ についてだが,次のような関係になっている. よって $λ_{+z}$ というのは |m,s>} を |m-1,s+√3 >} に変化させる働きがあることが分かる. $λ_{-z}$ については省略するがこれとは符号が逆になる.

,,というのは,ウェイト図の上での次のようなベクトルを意味していたことになるわけだ. 図で表すと次のようである.

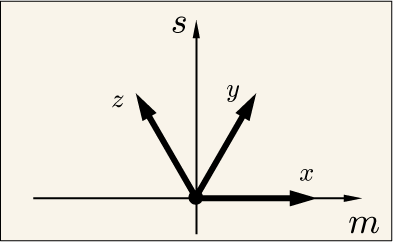
ウェイトを上げ下げする行列がどのようにウェイトを上げ下げできるかをウェイト図の上に表した図

6 つの行列による固有値変化の行き先を全て描くと次のようになる.

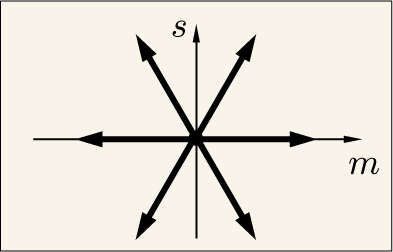
ウェイトを上げ下げする全ての行列がどのようにウェイトを上げ下げできるかをウェイト図の上に表した図

このようなものを「ルート図」と呼ぶ.ウェイト図に描かれる点は固有ベクトルの存在を意味しているわけだが,ある点からこのようなベクトルで示される移動をした先には別の点が存在し得ることになる.しかし固有ベクトルの数は有限なので,やの値にも上限や下限があるはずだ.今回のような状況では,つまり SU(3) では,どのように定めればいいのだろうか.

8 次元表現のウェイト図

8 次元表現があるということは,ウェイト図の上で三角形を並べていったときに,その頂点が 8 個あるように表現できるということだろうか？しかしそのようなものを試しに描いてみても,どうにも配置が非対称というか,不自然になってしまう.

こうなったら具体的に 8 次元表現を作って調べてみよう.「交換関係の秘密」のところで書いたように,行列 S_a の (b,c) 成分を次のように定めればいいのだった. 全部を書き出す必要はない. S_3 と S_8 があれば,そこから固有値を取り出せるはずだ.前回求めた構造定数のうち,添字に 3 を含むものと,8 を含むものだけに注目すればいい. ああ,そうか,今回は対角行列にはならないのだな.ゲルマン行列では構造定数 $f_{abc}$ の添字には同じ数字が入らないのだったから,それを利用して作った行列では対角成分は必ず 0 になるのだ.思ったほど楽には行かない気がしてきた.とりあえず,この二つの行列の積を計算してみて S_3 S_8 と S_8 S_3 が同じになることは確認してみた.この二つの行列は交換可能だ.

それぞれの行列の固有値と固有ベクトルを求めてみよう.まずは S_3 の方から. 固有ベクトルは規格化していない.その方が見やすいだろう.区別しやすいようにそれぞれのベクトルにアルファベットを割り振った.

次は S_8 についてもやってみる.同じベクトルには同じ記号を振っておいた. とはどちらも固有値が同じで,これらの線形結合をして新たなベクトルを作ったとしても同じ固有値なのだから,代わりにとを使ったとしても不都合はない.というわけで,どちらからも共通の 8 つの固有ベクトルが出て来たわけである.これらのベクトルのウェイト図を描いてみよう.

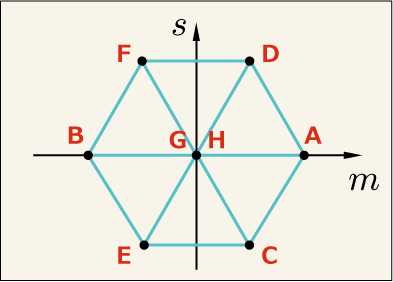
なかなか美しい！やはり三角形が基本となった配置をしている.このような規則的な配置を取るのはとても神秘的というか,不思議なことに思える.

しかしとがどちらも図の中央に位置しているのが気になる.これらは S_3 に対しても S_8 に対しても全く同一の固有値を持ったベクトルだというわけだ.同じものが二つあるのは無駄であるような気もする.どちらか一方を無くして 7 次元表現を作ったりはできないのだろうか？あるいは,G と H のベクトルを線形結合して作られるベクトルの自由度があることが重要な役割を果たしていたりするのだろうか.

状況はイメージできるようになったが,余計な疑問が増えてしまった.

実験

図の上に重なって存在している固有ベクトル G と H の役割があるのかないのか,その構造を明らかにしてみたい.例えば,もし G に対して $λ_{+x}$ を掛ければ,ベクトル A になるのだろう.H に対して同じことをすればやはり A になるのだろうか？逆に A に対して $λ_{-x}$ を掛ければ,その結果は G になるのであろうか,H になるのであろうか.一体どちらに戻るのだろう？あるいはどちらにもならずに,両者の線形結合になったりするのだろうか？

それが分かったとしても,他の方向でやってみたならどういう違いが出るだろうかという疑問も出てくるだろう.結局, S_3 と S_8 だけでなく,全部を作ってみる必要が出て来てしまったではないか.

実際にやってみたが,単調作業で面倒なので,結果だけ書き連ねることにしよう.

G は A に移動できた.しかし,H を A に移動しようとしたら,0 になってしまった.A を元に戻そうとすると G に戻った.H の存在の意味はまるでないかのようだった.

G は B に移動できた.しかし,H を B に移動しようとしたら,0 になってしまった.B を元に戻そうとすると G に戻った.ここまでのところ,H の存在の意味はまるでないかのようだった.

G は D に移動できた.今度は H も D に移動できた.G も H も,どちらも D にも E にも移動できた.さっきとは違っている.戻してやるとどうだろうか.D は G + H という,両者が混じったベクトルに戻ってきた.E も同じだった.

残った方向も試してみよう.G も H も,どちらも F にも C にも移動できた.戻してやると,F からも C からも,G - H という,両者が混じったベクトルに戻ってきた.

まったく意味が分からない感じがしたが,何となく規則性が見えてきた.まるで,120°対称な方向へ向かう 3 つのベクトルの,縦横比のようではないか.横軸へ向かうベクトルにとって,縦の成分は 0 であり,120°の方向へ向かうベクトルにとって,横は 1,縦はであり,240°の方向へ向かうベクトルにとって,横は 1,下向きにである.

ここまでベクトルを規格化しないで考えてきたため大雑把にしか分からないが,符号などにも注意すればちゃんとした図形的に対称な規則が成り立っているのかもしれない.しかし今回はこれくらいにしておこう.

SU(N) の随伴表現のウェイト図はルート図と同じ形状になるという話を聞いたことがある気がするが,それが本当なのか,他の群の場合にどうなっているかを調べている余裕は今のところはない.もう少し先を調べれば,その辺りの手掛かりがつかめるかも知れないと思っている.