SU(3)の全貌を知りたい
まだしばらくは SU(3) の話が続く.ウェイト図の上に三角形を並べていけば何次元表現が可能かが分かるという信頼は打ち砕かれてしまった.8 次元表現のウェイト図は三角形の頂点を数えたならば 7 つしかないが,中央に位置するベクトルが二つ重なって存在しているので 8 次元なのだった.どういう場合にこういうことが起きるのかをはっきりさせたいと思う.
教科書で見かけるものは,8 次元表現や 10 次元表現,15 次元表現だが,それ以外にもありそうな気はする.
しかしなぜか見かけた試しがない.何らかの理由で制限されていて,実際は存在し得ないのだろうか?それとも,ただ面倒だから,教科書では応用例が多いものだけを選んで載せているのだろうか?
三角形を並べると言っても,どんな並べ方が許されるのだろうか?対称的に並べたらそれでいいのだろうか?六芒星のような並べ方は許されるだろうか?
記号や用語の変更
この後の説明のために,ここまで使ってきた用語や記号を少し改めよう.独自の記法を貫くと不便なので,リー群論の教科書でよく見られる書き方に従うことにする.
ここまで二種類のウェイトを取り出すために使っていた行列と
をそれぞれ
,
と表記することにする.そして,ウェイトの上げ下げに使っていた
などをすべてひっくるめて,
と表すことにする.
の部分がルートベクトルを表していて,そこは
かもしれないし,
かもしれないし,
や
などかもしれない.その中身で区別するのである.
にはリー群論の中では特に呼び名があるようには思えないのだが,物理の方から名前を借りて,ここでは「昇降演算子」と呼ぶことにしよう.物理では角運動量の上げ下げに
や
を使うが,これらをそれぞれ「上昇演算子」,「下降演算子」と呼び,二つまとめて呼ぶときには「昇降演算子」という用語を使うのである.さすがに SU(3) ではウェイト図の中で色んな方向に移動するので上がったり下がったりするだけではないのだが,なぜか適切な名前が用意されていないようなのである.「移動演算子」などと命名したいところだが,勝手に名付けるわけにも行くまい.
これまでや
の固有ベクトルを
と表してきたのだった.
が
の固有値を表していて,
が
の固有値を表しているのである.しかしこれも改めて
と表記しよう.
というニュアンスである.
色々と変更をして申し訳ないが,あと少しだけ.これまで物理用語との混同をなるべく避けて来たのだが,便利なので使いたい用語が幾つかある.
これまでのことを徹底して固有ベクトルと呼んできたわけだが,時々は「状態」と呼ぶことを許してもらいたい.量子力学では固有ベクトルの一つ一つが物理的に異なる様々な状態を表しているわけだが,そのニュアンスだ.ウェイト図の上に並ぶ一つ一つの点のことを「状態」と呼びたいのである.「ウェイト図の上にどのような状態が存在し得るか」などという言い方を使えたらわかりやすく話せる気がする.
また,ウェイト図の同じ点に二つ以上の状態が重なって存在していることを「縮退」と呼びたい.これは全くの量子力学の用語であって数学用語ではないのだが,状態が重なって存在しているニュアンスを一言で表すのにこれほど便利な用語を他に知らない.
漸化式を作ってみる
ある状態に対して昇降演算子を作用させることで,ウェイト図の上を移動させることができるのだった.その様子を数式で表すと次のようになる.
というのは何らかの定数である.ベクトル
はどれも規格化されているものを考えることにしたいのだが,昇降演算子を作用させた結果として出てくるベクトルはそのままでは規格化されているわけではないので,調整するための定数が必要なのである.その定数はどの状態に対してどの昇降演算子を作用させるかによって異なるのだが,作用させる前の状態のウェイト図上での位置
と昇降演算子のルートベクトル
の二つを指定することで区別して表そうというわけだ.
SU(3) を表現する行列として何次元のものが許されているかを知りたいわけだが,有限次元なのだから,や
の値には上限や下限があるはずであろう.ウェイト図の原点から一番外側に離れたところにある状態に対して,さらに外側へと移動させようとして昇降演算子を作用させた場合には,
となってくれなくてはならない.つまりそのような場合には,
が成り立ってくれているべきだということだ.
ここから話を先に進めるためには,昇降演算子どうしの交換関係を把握していないといけない.実は巧く話を進めると,次のような関係が成り立っていることが言えるのだ.
また,
の場合には次のような関係が成り立っている.
該当する
が存在していなければこの右辺は 0 になる.
の部分は定数であり,ちゃんと求めるための方法があるが,今回の議論ではあまり必要ではない.これらの証明は後回しにしよう.
(2) 式の両辺にを両側から作用させてみる.
まず右辺から計算してみよう.
とすると,この計算の意味は大して難しくない.
次は (4) 式の左辺だが,この計算のためには (1) 式のエルミート共役を取って作る次のような関係式を使う必要がある.
それで,(4) 式の左辺は次のように変形できる.
つまり (4) 式からは次の式が得られる.
ここにもう少しだけ変更を加えたい.左辺第 1 項の
の部分は次のように変形できる.
それで (5) 式は次のように書ける.
この式のどこが素晴らしいかというと,
の絶対値が分かれば
の絶対値が求まるので,ある状態
に対して
を作用していった結果に付けるべき係数が次々と求まるということである.規格化をするときには位相は好きに選んだらいいので,絶対値さえ得られればそれでいいのである.
先ほど,や
には上限や下限があるべきだという話をした.今,ある状態
に対して
を
回作用させることでその上限の状態に到達したとしよう.すると
は存在しているがその先はないのであるから
であろう.ここから始めて (6) 式を順次適用していけば・・・.つまり,まず初めにこれを (6) 式の第 2 項だと考えて当てはめてやれば,
が得られるだろう.こんな調子でどんどん
を作用していった時の係数が導かれることになる.それがどこまで続くかと言えば,どこかで下限に達するわけだから,
に対して
を
回作用させた時点で訪れたとしよう.そこに至るまでに行うことになるだろう計算を全て並べると次のようになる.
この計算は多くを解決するかのように見えて,肝心な部分で実用性を欠いているように思われる.計算の起点に選んだ
というのがウェイト図上のどこであるかが指定されていないし,そこから両方向へそれぞれ何ステップまで状態が存在するかという
と
という値は勝手な仮定でしかなくて,それを決定する方法はまだ知らないし,しかもウェイト図上を一方向へ進み続けることしか考えられていないから,平面的に広がるウェイト図の全体の様子を調べ尽くせるとは思えない.しかしこの後で意外な視野が開けてくるのでもう少しだけ我慢してもらいたい.
この多数の式を全て足し合わせてみよう.ほとんどの項は打ち消し合って消えるはずだ.いや,左辺は全部消えてしまうな.全部で個の式があるわけだから,右辺も意外と簡単な式にまとめられる.
も
も 0 以上の整数という設定なので,
の部分は決して 0 になることはなくて,
という関係式が得られる.ここで関係式を簡略化するために
だと仮定しよう.つまり,起点となる
はそれ以上に上の状態がないような状態だと仮定することを意味する.ウェイト図に並ぶ多数の状態の中で一番端っこに位置するどれかだということだ.そしてそこから
を使って移動して行き,
ステップまでは状態が存在するということになる.式はこうなる.
この関係式では,ウェイト図の上で移動する方向は
だとしているわけだが,SU(3) の場合には 3 通りの方向があるのだった.つまり,(8) 式と同じ形の式が 3 通り作れるのではないだろうか.もちろん
は方向ごとに異なるから,区別する必要があるだろう.
この 3 つの整数
,
,
を定めて,この関係式を連立させて解いてやれば,
が求まるのではなかろうか.つまり,起点とすべき状態
の座標が導き出せるはずである.いや,待てよ.SU(3) の場合,ウェイト図は 2 次元平面上なのだから,座標を表す 2 つの値が特定できればいい.式は 3 つも要らないはずだ.2 つあれば十分である.例えば
と
の 2 つを決めてやるようにすればれば
が求まり,
はそこから勝手に決まることになるだろう.
最高ウェイト、単純ルート
状況は以上のようなのだが,ウェイトの上限,下限という表現がかなり混乱してきている.例えばもしを使って上のようなことを考えた場合,
を作用させるごとに
の値は下がっていくが,
の値はむしろ次々と増加してくることになってしまい,下限というよりは
の上限を目指すことになる.
この辺りは単に言葉の問題に過ぎないわけだが,誰もが納得できるような統一基準を採用して状況の整理をしておこう.
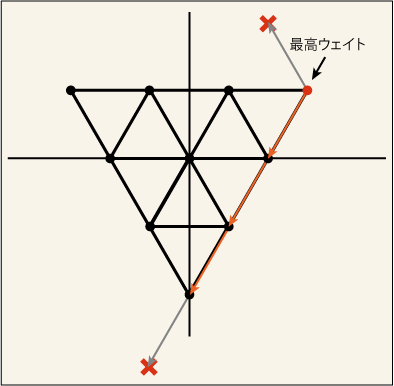
ウェイト図の上に並ぶ様々な状態の間に順序を決めることにする.右側にあるほど上位だと判定する.もし左右で決めることが出来なければ,その場合には上にあるものほど上位だと判定する.そのような基準で一番上位になっている状態のことを「最高ウェイト」と呼ぶことにしよう.
ルートについても基準を見直そう.右側を向いているものを「正ルート」,左を向いているものを「負ルート」と呼ぶことにする.右も左も向いていないものについては,上向きのものを正ルート,下向きのものを負ルートと呼んだらいいが,SU(3) の場合にはそのようなものはなかったのだった.
そして正ルートばかりを集めることにする.とは言っても SU(3) の場合は 3 つしかないわけだが,ここでは拡張の効く話し方をしておこう.ある正ルートが,「他の正ルートに正の係数を掛けて作った線形結合」として表せないとき,それを「単純ルート」と呼ぶことにする.これは線形独立なルートベクトルを選ぶのに似てはいるが,もう少し厳しい条件である.単に線形独立なルートベクトルを選ぶだけなら幾つかの選び方があるが,このような決まりを採用してやると,なぜかうまい具合に線形独立なルートの選び方の中の一つが定まることになるのである.
それがなぜなのかについて,少しだけイメージを話しておこう.先ほどウェイトの順序を決めたのと同じやり方でルートベクトルの順序を決めてやったとすると,単純ルートとして選ばれる可能性が高いのは正ルートの中でも下位のものである.単純ルートの候補は正ルートの中からしか選ばれないし,正の係数だけを使って単純ルートを組み合わせて他の全てのルートを表現することになるのだから,下位のものを足し合わせて上位のものが作られるという形になる可能性が高いわけだ.しかし下位から順番に必ず選ばれるわけではないことに注意しよう.基本的には下位から選んでいくことになるが,途中で候補から外れるものがチラホラと出てくるからだ.
SU(3) では 2 つの単純ルートが選ばれることになる.そして,単純ルートには下位のものから順番に番号を振るという約束にしておこう.前回はルートベクトルに,
,
という記号を付けて区別したが,そのような区別を一旦忘れて 2 つの単純ルートをそれぞれ
,
と表記しよう.次のようになる.
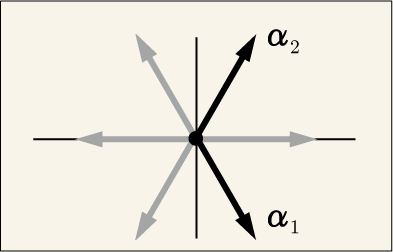
そしてこれらの単純ルートを使って先ほどやったような関係式を作ってやる.
これらを解いて導かれる
は実は最高ウェイトの座標である.なぜだか分かるだろうか.単純ルートは正ルートの中から選ばれたので,求めようとしている
というのは,それより右には状態が存在しないのであり,それはまさに最高ウェイトだというわけだ.
この 2 つの数値と
を定めることで,その状況に合った最高ウェイトの位置がただ一つ導かれることになる.この 2 つの数値を
のように並べて表したものを「ディンキン指数」と呼ぶ.一つのディンキン指数の組を指定することによって,一つの表現が定まるというわけだ.
実現可能な表現というのは,このディンキン指数で表される組み合わせの数だけ,つまり,無限に存在する.
最高ウェイトは縮退していない
これで必要な鍵は揃っただろうか?まだ縮退の問題が解決されていない.ウェイト図上のどこかに二つ以上の状態が重なって存在しているかも知れないわけだが,それをどうやって判定したらいいのだろうか.
とりあえず,最高ウェイトは決して縮退していないことを導くことができる.もし最高ウェイトの位置に異なる二つの状態が重なって存在しているとすれば,一方の状態に対して昇降演算子を次々と作用させてウェイト図上のどこかを一周するコースで元の場所に戻ってきた時に別の状態
になっている可能性があるということだ.
この右辺の昇降演算子の中には必ず正ルートが混じっていることだろう.なぜなら負ルートばかりでは決して元の場所には戻って来られないからである.正ルートの昇降演算子は (3) 式の交換関係を使って位置を交換して右側へと寄せてくることができる.こうして正ルートばかりが右側にあるという式に書き換えることができるわけだ.ところが最高ウェイトというのはそれ以上の状態が存在していないのだから,正ルートを作用させると 0 になってしまう.結局この式が意味するのは
であり,仮定したような状態は存在しないというわけだ.
こういうわけで,最高ウェイトには複数の状態が決して重なっておらず,安心してここを起点にして昇降演算子を作用させて次々と新しい状態を探してゆくことができるということになる.
さて,今の話は最高ウェイトが縮退していないことを説明していたが,この論理はもう少し広く使えて,ウェイト図を描くための重要なヒントをくれる.
最高ウェイトとトップの座を争ってギリギリで負けた別の状態があったとしよう.左右での判定では同順位だったが,上下の判定で惜しくも破れたのである.つまりそのような状態がもしあるとすれば,ウェイト図の上で,最高ウェイトの真下にある.そのような状態が存在するかというと,SU(3) の場合には存在し得ないのである.
理屈は先ほどとほとんど同じだ.SU(3) の場合,上下方向へまっすぐ進む単純ルートがないから,最高ウェイトからこの状態へと向かうためには一旦負ルートの昇降演算子で左へ移動してから正ルートで戻るしか道がない.これを交換関係を使って正ルートを先に作用させる形にすると 0 になってしまうし,負ルートだけになった項ではこの状態へと決して戻ってこれない.
これは SU(3) などの特殊な場合にだけ当てはまる話なので教科書ではわざわざ説明されていないことが多いが,SU(3) で全ての状態を探し出すためにはとても重要な条件である.
縮退の判定
では最高ウェイト以外の状態はどうかというと,縮退している可能性は高い.ある状態を始点にして別の同一のウェイトに到達するために二通りの道筋があるとき,例えば,
のような具合になっているわけだから,
となり,両ベクトルには何らかの差があることになる.とは言っても,これは必ずしも縮退していることを意味しているのではない.ここで (3) 式を使ったわけだが,この係数
は 0 であることもあるし,あるいはこの最終結果が
や
と平行になっている可能性もあって,その場合は
と
は同一であろう.
この辺りの判定法はの具体的な形を知っていないと使えないし,今はそれを求めるためにまず行列の次元の数を知りたいと思っているのだから,本末転倒である.あまり役に立ちそうにもない話に思える.
ワイル鏡映
ウェイト図を描くのに重要なヒントはまだある.ちょっと前に話を戻そう.
ある状態を起点にして,
なら
回,
なら
回作用させるところまでは何かしらの状態が存在するという仮定をして話を進めたのだった.だとしたら,ウェイト図上で
から
だけ離れた場所というのは絶対にこの範囲内にあるわけで,そこには確実に別の状態
が存在していることが言えるのである.
ごく当たり前のことであり,しかも
から
だけ離れた位置というものにそれほど重要な意味があるとも思えないので,今さらなぜこんなことを問題にするのかと思うかもしれない.ところがこの
と
の位置関係が面白いことになっているのである.この式に (7) 式を代入してやろう.
この式から何が言えるだろうか?
から
に向かって引いた直線,すなわち
というベクトルが
と平行になっているのは仮定そのまま過ぎて当然の話である.そうではなく,
と
の中点がどこを向いているかを調べてやろう.
これが中点を指すベクトルだ.これと
との内積を計算してやる.
と
を結んだ線がベクトル
に対して平行,かつ中点がベクトル
に対して垂直であるということは,ウェイト図の中心から,ルートベクトル
に対して垂直に伸ばした線を境界線として,
と
とが対称な位置にあるということである.このような性質を「ワイル鏡映」と呼ぶ.
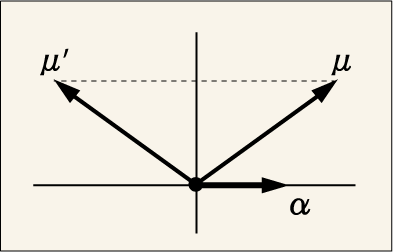
これはどの状態,どのルートベクトルに対しても成り立っているので,ウェイト図のどこかに状態があれば,対称な位置にも必ず状態が存在していることが言えるのである.
ウェイト図のどこかに状態がないと分かれば,対称な位置にも状態が無いということも言える.これは便利だ.
幾つかの実例
では,今までに導いた性質を使って,幾つかのウェイト図を作ってみることにしよう.
(9) 式にと
の座標を当てはめて,あらかじめ
の座標を導いておくと便利である.
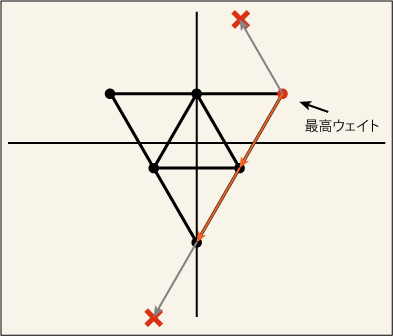
まずはディンキン指数 [0,1] から試してみよう.最高ウェイト
の座標は
となる. [0,1] というのは
方向には一歩も動けず,
方向には一歩だけ動けるという意味だから,どこに状態が存在していないかがすぐに分かり,さらにワイル鏡映の性質を使えば原点の周囲が状態のない部分に囲まれて,次のような図が書き上がる.
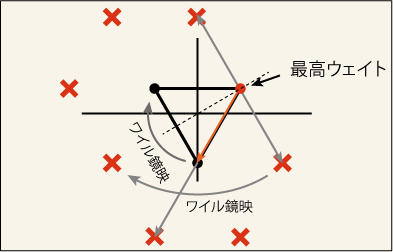
これは以前に一番最初に出て来た 3 次元行列による表現だ.リー群論では「3次元表現」という書き方はせず,「表現」と書く.
次に [1,0] を試してみよう.ほぼ同じだから説明は省略しよう.
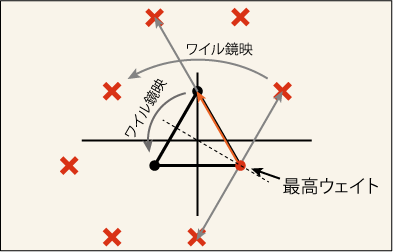
何だろう,これは?状態は 3 つしかないけれども,前に出て来た 3 次元行列による表現ではこのような固有値を取る状態は出てこなかったはずだ.前には見付け出せなかった,この状況に合う行列の作り方が他にあったのだろうか?それについては次回で考えることにしよう.これはリー群論では「表現」と書く.この表記から想像されるように,複素共役が関係しているのだ.
[1,1] にしてみたらどうなるか.
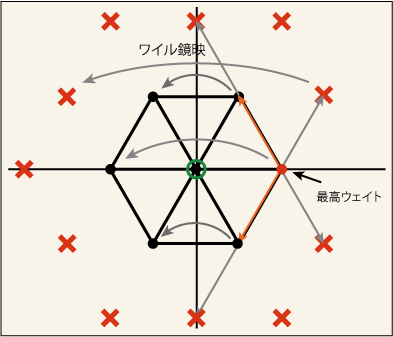
どうやらこれが以前にやった 8 次元の随伴表現に相当するらしい.「表現」だ.中央の状態がなぜ縮退しているのかは,ここまでの話だけから推定するのは難しい.
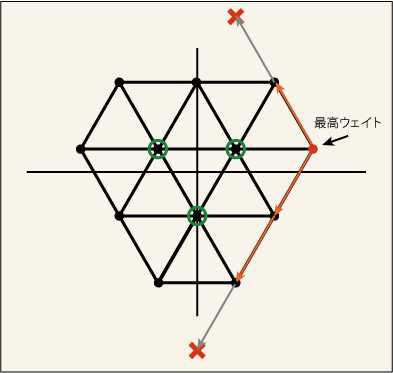
もっと数値を増やしてみよう.[0,2] だと次のようになる.
慣れてきたと思うのであまり多くを書き込んでいない.どうやら状態が 6 個あるように思える.どこが縮退しているのかは判定できないが,他の教科書から推定するところによると,この場合には縮退はどこにもないらしい.「表現」である.
これを [2,0] にするとこの図が上下さかさまの状態が描ける.図は省略するが「表現」である.
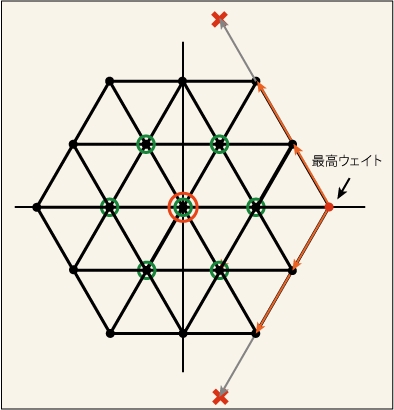
[1,2] は次のようになる.
中心に近い 3 つの状態がどれも 2 重に縮退していて「表現」なのだそうだ.[2,1] は上下が逆さまだから省略しよう.
[2,2] は「表現」
中心がなんと 3 重に縮退していて,その周りが 2 重に縮退しているからだそうな.そうなる理由もあとで突き止めねばならない.
[0,3] は「表現」
こちらは縮退はどこにもないそうだ.なぜなんだ?
これくらいにしておこう.何となくパターンが見えてきたようなそうでないような,微妙な感じだ.
諦めずに探検を続けよう
今回の話で使った昇降演算子の交換関係 (2) 式と (3) 式の証明を最後にやっておこうと考えていたが,もうかなり長くなってしまったし,今回だけで全てが解決しそうにないので次回以降に回すことにしてもいいだろうか.そのついでにルートベクトルについての性質をもう少し詳しく話しておくことも出来そうだ.
最初に持っていた疑問が解決しないばかりか,新たな疑問まで出て来てしまったが,もう少し進んでいけば分かるようになるだろうという希望は無くしていない.










