物理数学：ベクトル解析の準備

ベクトルを微分する

微分や積分の手法を使って関数を調べる数学分野のことを「解析学」と呼ぶ.「ベクトル解析」というのは微積分を使ってベクトルに関連した性質を調べるもので,ほとんど物理のためにあるような数学の応用分野である.

例えば,ベクトルを微分すればベクトルの変化が分かる.ベクトルを微分するなんて一体どうやるんだと思うかも知れないが,ベクトルの各成分が関数で表されているとすると,それぞれの関数を微分してやればいいだけである.

もう少し具体的なもので説明した方が良いだろう.時間によって変化するベクトル A(t) があったとする.これはつまり,各成分が時間の関数で表されていて,時間によって変化するということである. このベクトルを微分したものを dA/dt と書く.その意味は,次の右辺のように計算したものを表している. この dA/dt もまたベクトルであり,やはり時間によって変化するベクトルである.これはベクトル A(t) がどれくらいの割合で変化するかを表している.微小時間秒後にはおよそ dA/dt Δt だけ変化するのである.次のように書けるだろう. 少し前の偏微分の説明のところでもやったように,もし無限小の極限での時間変化を考えてそれをと表すなら,近似ではなく次のように表してもいいだろう. このように割りと単純な話である.今のところは・・・.

微分でベクトルを作る

ベクトル解析ではベクトルを微分するばかりではない.ベクトルではない一つの関数を色んな方向で微分することによって,新たにベクトルを作り出すこともする.

例えば土地の標高を表す関数があるとする.これを h(x,y) としよう.ととで平面上の一点の位置を指定することで,そこの標高を返すようになっている.

この関数をで偏微分したものと,で偏微分したものを並べてベクトルを作ることができる. このベクトルは一体何を表しているだろうか？最初の成分はこの土地を軸方向に移動したときの土地の傾きを表しており,もう一つの成分は軸方向に移動したときの傾きを表している.もし軸方向にも軸方向にも傾いているこの地面の上にボールを置いたなら,軸と軸のどちらの方向にも力を受けて,結局は斜めの方向に転がり出すことだろう.斜面の上で静かに置かれたボールは,傾いている方向へ向かって転がり始めるものである.要するにこのベクトルは「どちらの方向へ向かって最も傾いているか」を表しているイメージになっているのである.

しかしこのベクトルは,斜面に置かれたボールに働く力を表しているわけではない.もし断崖絶壁の急斜面に差し掛かったら,地面の傾きが無限大に近いからと言って,ボールに無限大の力が掛かったりするだろうか？そんなことはない.今の喩えが成り立つのは斜面が非常に緩やかなときだけだ.

それと,(1) 式が表すのは傾きが正になる方向なのだから,ボールが転がる方向ではなくて,その反対方向なのだった.そこにも注意が必要だ.

斜面でボールに働く力

脱線になるが,今の話が気になる人もいるだろうからどうしてそう言えるのかを簡単に説明しておくことにしよう.斜面に置かれたボールには重力が掛かっており,それは地面を垂直に押す力と地面に沿って運動を始める力とに分解できる.斜面の傾きをとすると,前者が mgcosθ であり,後者は mgsinθ である.

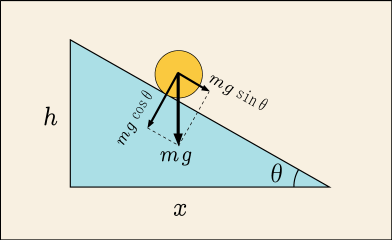
傾きが 90°になったとしてもボールを動かす力はせいぜい止まりであって無限にはならない.ではなぜ傾きが緩やかなときには先ほどの喩えがしっくり来るのか・・・？ sinθ をグラフにしたものを見ると,が極めて小さいところではほぼ直線に近いだろう.あとでテイラー展開を学ぶとはっきり分かるが, sin 関数は次のように展開できる. が極めて小さいところでは右辺の最初の項と次の項の差が大きいのでと近似できる.また斜面の傾きというのは先ほどの図の三角形の高さと底辺の比であって,それは tanθ と同じである. tanθ も同じ理屈でが極めて小さいところではと表せる.傾きが小さいところでは斜面の傾きも sinθ もに近い.

要するに,斜面の傾きが非常に小さいときに限ってはボールに働く力と傾きは比例すると言えるのであり,先ほどの喩えがとてもしっくり来ることになっているのである.

傾きの方向を表している

ということは,傾きが非常に大きい場合にはまだちゃんとした説明ができていないということになる.そういう場合でも (1) 式のベクトルが「斜面の傾きが最も大きくなる方向を示すベクトル」であることを,ちゃんと納得できるような説明を考えなくてはならない.

そういう部分を考えるのは読者に任せてもいいのだが,一応の模範解答みたいなものを書いておこう.本当に模範解答であるかどうかの保障はできない.

地点を (x,y) として,そこから (Δx,Δy) だけ離れた地点を地点とする.地点と地点の高さの差は次のように表されるだろう. もし無限小の極限を考えるなら,この近似は極めて正確になり,次のように表しても良くなる. 偏微分の記事の中で出てきた全微分と同じ形だ.この右辺は ( ∂h/∂x , ∂h/∂y ) というベクトルと ( dx, dy) というベクトルの内積になっている.内積というのは,二つのベクトルの方向が同じときに値が最大になり,その時にはそれぞれのベクトルの大きさを掛け合わせたものに等しくなるのだった.要するに, ( ∂h/∂x , ∂h/∂y ) が表すのと同じ方向へ向かって移動するとき,最も効果的に斜面を駆け登ることが出来るわけである.このとき, ( dx, dy) というベクトルの絶対値が真上から見たときの平面での移動距離を表しており,というベクトルの絶対値がもっとも勾配が大きな方向に向かうときの斜面の傾き具合を表している.

こうして ( ∂h/∂x , ∂h/∂y ) というベクトルが「最も傾きが大きくなる方向を示すベクトル」であることに疑いがなくなっただろう.

3次元への拡張

ここまでの話では,上から見た位置をとで指定することで,その地点での高さを返すような関数を例に使ったのだった.しかし物理学でよく使うのは,これを 3 次元に拡張したような概念である.3 次元内の点を指定すると,その点での何らかの値が返ってくるような関数を使うのである. それは例えば,ポテンシャル・エネルギーと呼ばれるようなものである.場所ごとに滑らかに変化する架空の数値が割り当てられているイメージである.それは先ほどの例での「高さ」のように目に見えるような量ではない.物体はこの値の傾きが最も大きくなるような方向に向かって力を受けると考えるのである.そんなとき,先ほどと同じように作った次のようなベクトルが役に立つ. このようなベクトルを数式の中に毎回書くのは面倒なので,ナブラと呼ばれる記号 $\nabla$ を使って,これと同じベクトルを $\nablaU$ と表すことが多い.つまり,こういうことだ. この $\nablaU$ のことを U(x,y,z) の「勾配」あるいは「グラーディエント」(gradient)と呼ぶ. $\nablaU$ と書く代わりに gradU と書く場合もある.

ここではわざわざ U(x,y,z) と書くのが面倒なので変数を略して $\nablaU$ などと書いているが,もちろん, $\nablaU(x,y,z)$ や gradU(x,y,z) などと書いても良いのである.

さて,先ほど話したことを $\nablaU$ を使って表現してみよう.物体に働く力を 3 次元ベクトルで表すことにする.物体にはポテンシャルエネルギー U(x,y,z) が小さくなるような方向に向かって力が働くのだが, $\nablaU$ というのは傾きを登るような方向を指しているので,そのままではダメだ.マイナスを付ける必要がある.次のように表せば良い. 左辺のは,空間の各点で物体が受ける力を意味している.場所によって力の働く向きが違ってくるわけで,このベクトルも場所によって定まる「場所の関数」だと言えるだろう.だから次のように書くこともある. ここで出てきた「ナブラ」だが,竪琴を意味するヘブライ語に由来するギリシャ語なのだそうだ.竪琴に形が似ているというのでそう呼ばれるようになったのである.ただの逆三角形だけれども.

ベクトル場

急いで色々と話し過ぎた感じもするのだが,まだ「ベクトルを微分する」話と,「位置が変数になっている関数からベクトルを作り出す」話をしただけである.もう一つだけ話しておけば大切な概念が出揃うことになるので無理して聞いてもらいたい.

「位置の関数になっているベクトル」というものを考えることができる.3 次元空間で考えるなら,位置を表す (x,y,z) の 3 つの変数によって,ベクトルの軸,軸,軸の各成分が全て決まるという話であるから, という形になっているベクトルを考えることに他ならない.これは,空間内での位置を指定してやれば,それに応じたベクトルの方向と大きさが決まるというものである.空間がベクトルを表す矢印でびっしり埋め尽くされているようなイメージである.

科学館などの展示で,巨大な磁石の周りに,小さな方位磁針がびっしり並べてあるのを見たことがあるだろうか.あるいは子供向け図鑑などで,地球が巨大な磁石であること表すために,似たような図が描かれていることもある.それらは磁場を可視化するために工夫したものである.磁場の他にも,電気力の場,すなわち電場,重力の場,すなわち重力場などのような「場」が色々とある.それらはその地点で物体に働く力の方向をベクトルで表したものである.

しかし「場」は力を表すものばかりとは限らない.空間内の位置によって定まるベクトルは色々な場面で登場し,応用される.そのような性質を持つベクトルをひっくるめて「ベクトル場」と呼ぶ.そう言えば先ほどの話に出てきた F(x,y,z) というのもベクトル場の一種である.

ちなみに,先ほど出てきた U(x,y,z) のように「位置によって一つの値が決まる」ものは「スカラー場」と呼ぶ.ベクトルは「大きさと方向を持つ量」だが,それに対して「大きさのみを持つ量」のことをスカラーと呼ぶのである.

注意：ベクトルの定義には幾つかあって,それぞれ少しだけ守備範囲が異なっている.「ベクトルとは何か」と聞かれて「大きさと方向を持つ量です」と答えると,場面によってはダメ出しを食らうことになる.例えば線形代数でのベクトルの定義はすでに話したが,かなりイメージの異なる抽象的な定義だっただろう.その他の定義についてはいずれ必要になったときに話すから今はこの程度の説明で軽く流すことにしよう.スカラーについても同様であり,もう少し厳しい定義もあるので,ここでの簡易な説明を鵜呑みにしてはいけない.

補足：ベクトル場の各ベクトルは場所に固定されているものであり,異なる場所にあるベクトルどうしの和を取ることはできないし,やっても意味が無い.線形代数での「ベクトル空間の公理」による定義ではベクトルどうしの和が定義されていないといけなかったから,その意味ではベクトル場のベクトルはベクトルとは認められないことになる.しかしそれで不都合は起こらない.ベクトル場とは何か,と言えば,それは例えば「ユークリッド空間からベクトル空間へと対応させるような関数」であるとして捉えればいいだけである.

次回からはベクトル場についての計算をするときの公式をあれこれ紹介して行くつもりだが,物理では現実の 3 次元世界で起きている現象を扱うことが多いので,3 次元を前提とした公式ばかりが出てくることになる.もちろん物理では 2 次元のベクトル場を考えることもあるし,4 次元以上のベクトル場を考えることもある.とは言うものの,2 次元は単純すぎるし,4 次元は複雑過ぎる.まずは 3 次元で慣れることにしよう.