量子力学：2入力量子ゲート

制御ユニタリゲート

今回は 2 入力 2 出力の量子ゲートの話である.これは「制御ユニタリゲート」という名前で一括りにしてしまえる.

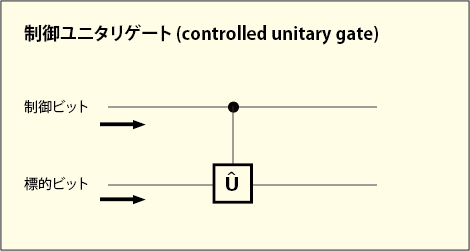
入力のうちの一方は「制御ビット（コントロールビット）」と呼ばれており,何の変化も受けずにそのままの状態で出力される.もう一方の入力は「標的ビット（ターゲットビット）」と呼ばれており,制御ビットの内容によって行われる操作が違ってくる.とは言っても非常に単純な話であって,もし制御ビットが |0>} なら標的ビットの方も何の加工も受けずにそのまま出てくるが,もし制御ビットが |1>} ならゲートごとにあらかじめ定められたユニタリ変換 $\hat{U}$ が施された状態で出てくる,というそれだけである.

もし制御ビットが |0>} と |1>} の重ね合わせだったなら,標的ビットは,加工を受けなかった場合と受けた場合との重ね合わせになるのだが,実はそんな簡単な説明で終わらせていいほど単純ではない.ちょっと予想外だと思うようなことが起きているのである.

それを説明するにはもう少し簡単なところから始めた方がいいだろう.制御ユニタリゲートの中でもかなり単純で,しかも良く使われるものがある.「制御NOTゲート」あるいは「CNOTゲート」と呼ばれるものである.CNOT というのは Controlled-NOT という意味である.

CNOTゲート

CNOTゲートというのは制御ビットが |0>} なら何もしないが,制御ビットが |1>} なら標的ビットの |0>} と |1>} とを反転させるという機能を持つゲートである.反転というのは,標的ビットがもし |0>} なら |1>} になって出ていくし,もし |1>} なら |0>} になって出ていくということで,古典的なNOTゲートに似ている.

もう少し一般的な表現をしておこう.標的ビットが次のような状態だったとする. もし制御ビットが |1>} ならば,この状態は反転されて次のような状態になって出ていく. 実はこの反転というのは前回の話で出て来た「Xゲート」と同じ働きである.前回は言い忘れたが「Xゲート」は「NOTゲート」と呼ばれることもある.

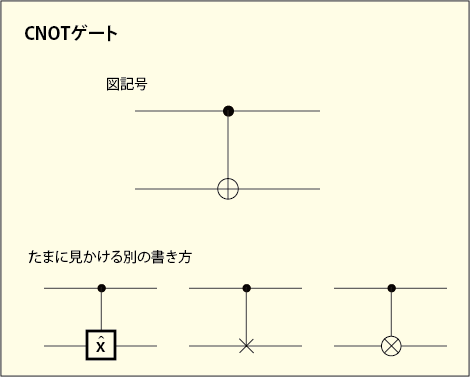
この図記号の意味だが,古典的な論理での排他的論理和を計算するときに使われている $\oplus$ という記号が由来である.二つの入力がともに |0>} のとき,ともに |1>} のときに標的ビットの出力が |0>} になり,一方が |0>} で他方が |1>} のときに標的ビットの出力が |1>} になる様子がまるで XOR ゲート（排他的論理和ゲート）の動作を思い出させるからである.たまに見かけることがある他の書き方は「制御Xゲート」であることを意味しているのだろう.

さて,細かい話はこれくらいにして,本題をさっさと話すとしよう.制御ビットが 1/(√2 ) (|0>}+|1>}) で,標的ビットが |0>} だったとする.つまり,半々の確率で標的ビットは |0>} のままか |1>} に変わることになるだろう.するとそれは結局のところ,標的ビットはと表せる状態になっていそうである.ところがそうではないのだ.もはやこの制御ビットと標的ビットはそれぞれ単独では表せない状態になっているのである.

このゲートを抜けてきた制御ビットを観測すると半々の確率で 1 か 0 が出るのだが,もし 1 が出たら,標的ビットを観測した時も必ず 1 が出る.もし 0 が出たら,標的ビットも必ず 0 として観測されるのである.要するに,「制御ビットが |0>} だったので標的ビットがそのまま |0>} として出て来た世界」と「制御ビットが |1>} だったので標的ビットが反転して |1>} になった世界」との重ね合わせになるわけだ.我々としてはそのどちらかの世界の一方を観測することになる.

制御ビットと標的ビットがそれぞれどちらも 1/(√2 ) (|0>}+|1>}) となって出てきているならこんな観測結果にはならない.どちらも 0 と 1 が半々の確率で出るのだから,観測結果としてはあらゆる組み合わせがありうるはずだが,そうはならないのである.だから,この不思議な状態を表すためには何かもっと別の表現を使う必要がある.制御ビットの状態 |ψ_c>} と標的ビットの状態 |ψ_t>} を並べて組にしたものを一つの状態 |Ψ>} とみなすことをしてみよう. もしそれぞれの状態がとなっていたら, のように表せるだろう.これは |0>}|0>} と |0>}|1>} と |1>}|0>} と |1>}|1>} の 4 つの状態の重ね合わせになっている.ところが今回の場合にはという特殊な状態が出来上がったと言えるのである.何が特殊かと言えば,この状態は |ψ_c>} と |ψ_t>} の積という形では表せないというところだ.(1) 式と(2) 式とを両立させる a,b,c,d の組がないことを確かめてみればいい.つまり, |ψ_c>} と |ψ_t>} の二つの状態は分けて考えることができず,一つの状態 |Ψ>} を共有しているのである.このような状態を「エンタングル状態」と呼ぶ.

最初に「制御ビットの状態 |ψ_c>} は何も変化を受けずに出てくる」と書いたが,どうやら訂正しなければならないようだ. |ψ_c>} と |ψ_t>} の状態をそれぞれ独立して記述することができなくなる場合があり得るらしい.つまり, |ψ_c>} だけを取り出してくることがそもそも無理で,そんなときには「入力と同じままだ」などと言うことが出来ない.そんな場合もあり得るのではないだろうか.

数式的理解

この少し奇妙な制御ユニタリゲートの機能を行列あるいは演算子の形で表してみたい.そうすればどんな入力に対してどんな出力があるのかを計算によって統一的に検証できて,全体像を把握しやすいのではなかろうか.先ほどのCNOTゲートの話ではたまたまエンタングル状態になる例を選んでしまったのかもしれないし,入力パラメータを様々に変えると何が起こるかをちゃんと知っておきたい.

最初の説明では独立した制御ビットと標的ビットがそれぞれ入力されるかのように話したのだが,どうやら両方を合わせて一つの状態となったものである |Ψ>} が入力されて,それが加工されて出ていくというイメージを持っていた方がいいのかもしれない.一つの制御ユニタリゲートから出てくる 2 本の出力がエンタングル状態になって出てきて,その 2 本がそのまま別の制御ユニタリゲートの入力になる場合もあるだろうからだ.

既に話したように,二つの量子ビットを一組にした状態というのは, |0>}|0>} と |0>}|1>} と |1>}|0>} と |1>}|1>} の 4 つの状態の重ね合わせになっている. ただしこの係数は次の条件を満たしている. (1) 式のようにして |Ψ>} を作った場合にはこの条件が自動的に満たされるようになっている.難しくはないので,もし暇なら確認してみてほしい.

この (3) 式の |Ψ>} は |ψ_c>} と |ψ_t>} の積として表すことが出来る場合もあればそうでない場合もある.それでも二つ並んだベクトルの前の方は制御ビットの状態で,後の方は標的ビットの状態である.制御ユニタリゲートの作用は,この状態 |Ψ>} に対して働く次のような演算子として表現すればよい. この |0>}<0|} や |1>}<1|} の部分は制御ビットの方にだけ作用する演算子であり, $\hat{I}$ や $\hat{U}$ は標的ビットの状態だけに作用する演算子だと決めておこう. $\hat{I}$ というのは恒等演算子,つまり何も変化させない演算子で,単位行列のようなものである.

<0|} や <1|} というのはこの量子コンピュータの記事では初めて出てくるものだから簡単に説明しておく必要があるかもしれない. <0|} はベクトル |0>} を転置して複素共役を取ったものである. |0>} が縦ベクトルだったから <0|} は横ベクトルであり, |0>} の成分は簡単に実数に選んでおいたから複素共役を取っても変化がない. <1|} も同じようなものである.だから具体的には次のようなものであると考えてもらっていい. これらには次のような関係がある. これは普通に行列の計算をすれば確かにそうなっていると確認ができる.なるほど, |0>}<0|} の右に |0>} が来ると |0>}<0|0>}=|0>} となって |0>} だけが残るし,右に |1>} が来ると |0>}<0|1>}=0 になって項ごと消えてしまう仕組みなわけだ. |1>}<1|} についても同様で,右に |1>} が来たときだけ項が生き残って,標的ビットに対して $\hat{U}$ が実行されるのである.

|0>}<0|} や |1>}<1|} は行列のようなものだとも考えられる. これも普通に行列の計算をすれば確かにそうなっていると確認ができる.

興味本位でCNOTゲートを全て行列で書いてみよう. $\hat{U}$ の代わりに X ゲートの演算子 $\hat{σ}_x$ を使うのである. これはこれ以上計算して簡略化しようとしてはいけないものである.各項の左側の行列は左側の状態にだけ,右側の行列は右側の状態にだけ働きかけるものだからである.つまり,次のような感じに使うのである. これを使って何を試せば自分としては納得が行くだろうか.

CNOTゲートを調べる

まずはエンタングル状態にない入力を試してみよう. |m>} が制御ビットで, |n>} が標的ビットだという想定である.これを (4) 式に代入すれば次のようになる. なんだか良く分からないし,自分はこれで何をしたかったのだろうかと立ち尽くしてしまうような結果だ.ああ,思い出した.このようにCNOTゲートを通した結果が「制御ビットと標的ビットの積という形で表せる場合」と「そうではなくエンタングル状態になる場合」の違いがどこにあるのかを知っておきたかったのだ.どうすればいいだろうか？

積で表せる場合というのは (1) 式のようになるはずだ.ところが今の結果の (5) 式はそれとは微妙に違っている.(5) 式が (1) 式の形式で表せる条件を知る必要があるが,両方の式が係数に同じ記号を使っているのが問題である.それぞれで違う記号を使って比較すればいいのだが,変数の数が多すぎて面倒くさい.そこで,うまくサボることを考えよう.まず,制御ビットが重ね合わせ状態でない場合はエンタングル状態にならないのは分かるので除外して考えることにしよう.また標的ビットが重ね合わせ状態でない場合のことも先ほど考えたし,それほど複雑ではなかった.制御ビットが重ね合わせ状態ならエンタングル状態になるのだった.そういうわけで,もっと面倒な場合だけに絞って考えてみることにする.つまり,制御ビットも標的ビットも重ね合わせ状態にある場合に限って調べるのである.規格化のことは後で調整してやればいいだけのことなので, a=1 , c=1 と仮定した上で考えてやればよくなる.つまり (5) 式はと表され,一方の (1) 式はという形式で表される.これらが同一になる条件を探ろう.と言っても,ここまで来ればもう簡単な問題であり,結果だけ書いてしまうと, t=1, b=s, d=1 となる場合と t=-1, b=-s, d=-1 となる場合の二通りしかない.

前者はこういうことだ.規格化はせずに書くが, という入力に対して出力はとなり,これはの積として書ける.要するに,制御ビットも標的ビットもどちらも何も変化せずに出てくるパターンだ.は複素数であり,規格化もしていないのだから |ψ_c>} としてはあらゆる状況が当てはまる.つまり標的ビット |ψ_t>} がこの形をしているときに限っては,制御ビットがどんな形をしていようが関係なく何も起こらないということである.考えてみれば当たり前なのかもしれない.標的ビットがこの形なら,反転させても何も変化しないのだから.

次に後者を考えてみよう.こちらはという入力に対して出力はとなり,これはの積として書けるということだ.入力の |ψ_c>} のにマイナスが付いているが,は複素数でどんな数でもいいので,実はあらゆる状況が当てはまる.つまり標的ビット |ψ_t>} がこの形をしているときに限っては,制御ビットがどんな形をしていようが関係なく,制御ビットの方の位相が逆転するということである.なんと,標的ビットは変化しないで,制御ビットの方が変化を受けて出てきてしまうのだ！

こうして,制御ビットは変化しないという最初の説明は便宜的なものであって,全く正しくないことが分かる.とは言っても,こんな劇的なことが起こるのはこのような特殊な場合だけである.

そして,これら以外のほとんどの場合には制御ビットと標的ビットの状態は分離して考えることが出来なくなるわけである.

もう少し調べてみる

既にエンタングル状態にあるものがCNOTゲートに入力されたら,何か面白いことが起こるのだろうか？その辺りも試しておこう.エンタングル状態とそれ以外の状態を判断するのは面倒なので,あらゆる状況を表した (3) 式を使ってみよう.つまり,(4) 式に (3) 式を代入するのである. こうしてみるととても単純である.第 3 項と第 4 項の係数が入れ替わるだけだ.分かりやすい法則だが,これだけのことに何か面白い応用があったりするものだろうか？

交換ゲート

3 つのCNOTゲートを次のように接続してみよう.

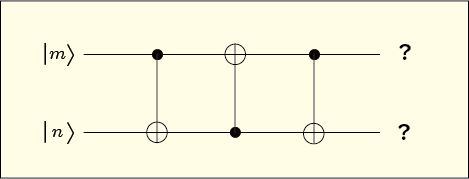
2 段目では制御ビットを標的ビットとして入れて,標的ビットを制御ビットとして入れている.とてもややこしいことが起こりそうだ.

ところがそうでもない.これまでは |Ψ>} を表す時に制御ビットの方を先に書くという考え方をしてきたのだった.しかしその考え方に縛られるのはやめて,図の上側にある量子ビット |m>} を先に書いて下側にある量子ビット |n>} を後に書いて全体の状態を |m>}|n>} と表すという考えに移行してみよう.その上で (6) 式を見直してみる.

(6) 式では制御ビットが |1>} になっている項どうしの係数が入れ替わっていたのだった.今問題にしている 2 段目の逆立ちしたCNOTゲートでは制御ビットが後ろ側に書かれていることになるので,第 2 項と第 4 項の係数を入れ替えるようにすれば,ここで起きることが説明できる.

そこで全体で起きることを考えてみよう.最初は次のような状態だったとする. まず第 3 項と第 4 項の係数を入れ替える. これが第 1 のゲートを抜けてきた後の状態であり,(6) 式と同じである.次は第 2 項と第 4 項の係数を入れ替える. これが 2 段目のゲートを抜けてきた後の状態だ.そして再び第 3 項と第 4 項の係数を入れ替える.結果は次のようになるだろう. 結局,一番最初の状態と比べると第 2 項と第 3 項だけが入れ替わった形だ.これは,二つの量子ビットを並べる順を逆にしてみてから項を並べ替えたのと同じことでもある.つまり,それぞれの量子ビットの役割を入れ替えたことに相当する.

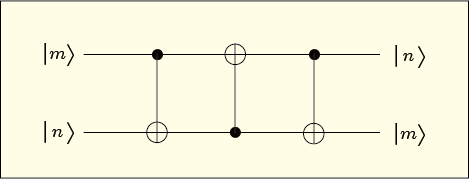
このようなゲートに通すと,二つの量子ビットの量子状態をすっかり入れ替えたのと同じことが起きるわけだ.この組み合わせで作ったゲートは「交換ゲート」あるいは「スワップゲート」と呼ばれる.

わざわざこんなゲートの組み合わせを使わなくても,ただ配線を入れ替えれば済むだけにも思える.しかしゲート式の量子コンピュータは量子ビットを保持した何物かを移動させる方式のものばかりではない.鎮座して在（ましま）す量子ビットに対して外から次々と働きかける方式もある.前者を「弾道型」,後者を「固定型」と分類したりする.

二つの量子状態を入れ替えるのにこのような方法もあるという提案は設計の幅を広げてくれるだろう.実用的な意味がなかったとしても,これはこれで理論的にも面白い.

毎回このような 3 つのCNOTゲートを描くのは面倒なので,交換ゲートを意味する次のような略記号も良く使われている.

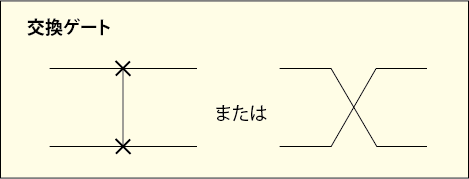
左側は制御 X ゲートが両方向に使われているといういかにも複雑な感じが出ているし,右側は経路を入れ替えれば済むだけだといういかにも軽い感じが出ている.しかしどちらも等価でありただの記号なので,微妙なニュアンスなどは気にしてもしなくてもいいので好きな方を使えばいいと思う.

万能性

ここまでCNOTゲートの話ばかりを書いてきた.しかしCNOTゲートは最初に話した一般的な制御ユニタリゲートのうちで最も単純な例に過ぎないというのだから,いかにもじれったく感じることだろう.

ところがそうでもなく,実はCNOTゲートと,1 量子ビットに対するユニタリゲートを組み合わせれば,どんな制御ユニタリゲートでも実現できてしまうのである.前回は 1 量子ビットに対するユニタリゲートは位相ゲートとアダマールゲートで実現できるという話をした.つまり結局のところ,位相ゲートとアダマールゲートとCNOTゲートがあれば,どんな制御ユニタリゲートでも作れてしまうのである.

具体的にどうやればいいのかと気になる人も多いと思うが,今回の話は既にかなり長くなってしまっているのでその話は次回にしよう.

ついでだからさらに衝撃的なことを先走って話しておこう.今のところ 2 つの量子ビットに対する操作の話しかしていない.しかし量子ビットの数がどれだけ増えても,それらに対するユニタリ的な操作はこれらのゲートの組み合わせで実現できることが知られている.

つまり,これで量子的な万能ゲートが出揃ったことになるわけだ.あとはもう読者の知恵と工夫次第でゲートを組み合わせて,どんな計算ができるか無限の可能性を追求してくれたまえ.……と言いたいところだが,それではあまりにも不親切なのでもう少し話が続くことになる.全部で 4,5 回の話にするつもりだったのだが,かなりの予定オーバーになりそうである.