相対性理論：クルスカル座標

亀座標

話を簡単に進めるために相変わらず dθ= dφ=0 として話を進めていこう.その場合にはシュバルツシルト解はこんな形になる. これを使って計算すると,場所によって光速の値が変化していることが導かれるのだった.しかしそれは無限遠にいる人の使う座標を基準にしているせいである.ブラックホールに落下して行く人にとっては目の前の光速は常にで一定なのである.

では何らかの新しい座標を導入することで光速が常に一定であるという結果が導けるようにできるだろうか.その座標は落下して行く人の視点に近いものになっているに違いない.このような座標を導入する魅力は,グラフに表したときに光の経路が斜め 45°の直線で表せることだ.

そのためには座標 (w,r) の代わりとなる新座標 (W,R) を使って, という形になるようにすればいい.光の経路では ds^2 =0 なので, と計算できるからだ.

関数 f(w,r) が旧座標を使って表されているせいで,(2) 式は新座標と旧座標が混在する形になっているが,そんなに気にすることではない.新座標と旧座標の関係が分かれば新座標に統一する形に書き直すのはいつだってできるからである.

f(w,r) としては色んなものが考えられそうだ.しかしとりあえず次のようなものを試してみよう. あまりややこしいことはしたくなかったのでには手を付けずにの方だけ新座標に変更して (2) 式の形を実現してみようというわけだ.しかしまぁ,これでもうまく行ってしまうのである.続きを見てみよう.これがちゃんとシュバルツシルト解と同じ意味になるようにするには (1) 式と比べてみて,次の関係が成り立っていればいい事が分かる. ここからとの関係を導いてみよう. プラスマイナスが出てきてどちらを選ぼうかと一瞬迷うわけだが,が増加する時にはやはりの方も増加してくれないと気持ちが悪いので,プラスの方を採用することにする.それでも r<a の範囲では右辺が負になるのでそこではとの増加量が逆転するだろうが,が無限大になるときにがマイナスの無限大に向かったりするよりはマシだろう. 単純な微分の式になった.両辺を積分すれば解決だ. これが新旧座標の関係である. r=0 のときに R=0 になるように定数を定めるとなので,次のようになる. こののことを「亀座標」と呼ぶらしい.ブラックホールへ落ちて行って動きが遅くなる人の立場に近い座標の取り方だからだろうか.とは言うものの,これは試しにやってみたらたまたまこうなったというだけの結果であり,物理的な解釈をして導いたわけではない.他の座標を選べる可能性だってあったわけだし,時間だって元の座標時をそのまま使っているのでブラックホールに落ちて行く人の立場を反映しているとは言い難い.

亀座標の意味を解釈することもなかなか難しいのである.との関係をグラフにすると次のようなことになっている.

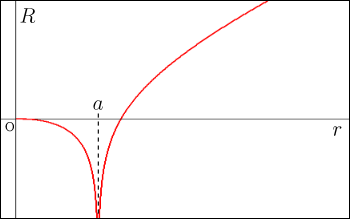
がから無限大にまで変化する間にの方はマイナスの無限大からプラスの無限大まで変化することになってしまっている.え,ちょっと待て！半径がマイナスだって？うーん.それはまぁいいや,無理に解釈しようとしないで数学上のものとして受け入れることにしよう.しかし r<a の領域で同じ範囲を共有することがどうも気持ち悪い.とが一対一対応になっていない辺りが単純なグラフ化を阻んでいる.

問題はさらにもう一つ.この亀座標を導入することで線素 ds^2 は (3) 式のように表されるようになる.もう少しすっきりまとめれば次のような感じだ. これを見ると r=a を境にして全体の符号が変わるという特異点のような振る舞いは相変わらず残っているのではないだろうか？どうしても消えないというなら受け入れるしかないが,どうなのだろう.

私ならこの辺りで諦めて,他にもっといい方法があるんじゃないかと道を引き返すところだ.しかしこのまま突き進んで問題を解決する方法があるのである.

クルスカル座標

これは重要なのだが,とりあえずはシュバルツシルト半径の外側に限定して話を進めよう.そして,次のような変換を使って (w,R) を新しい座標 (U,V) に置き換えることにする. この (U,V) を「クルスカル座標」と呼ぶ.この割りと単純に見える変換には色んな工夫が隠されているのだが,少しずつその全てが分かるように説明してゆくつもりだ.とりあえずは指数関数の肩の部分に注目してみてほしい.が正でも負でもどんな値を取ろうとも指数関数は正の値の範囲に限られる.よって常にである. (w,R) 座標を使ったままではの値がからへと変化するので,シュバルツシルト半径の外側の世界を表現しようとするだけでグラフの全域を使わざるを得なかっただろう.それをグラフの限られた領域へと押し込むことに成功したのである. (U,V) 平面にグラフを描くとしたらグラフの右下の象限に押さえ込んだ形になる.本当は 4 つある象限のどこに押さえ込んでも問題なかったのだが,右下に入れておくのがあとで図形的に分かりやすいことからそうしてある.

気になるのはこの変換を使った場合に線素 ds^2 がどう表されることになるか,だ.そのためにまず,,,の関係を計算する. この計算結果を眺めていると, dU dV という積を作るとすっきりしそうだ. この結果は (5) 式にぴったり当てはまる. この式にはととが混在しているので,(4) 式を使ってだけにしてみよう. ところで今はまだシュバルツシルト半径の外側の r>a の領域に限定して話をしているので,(7) 式の絶対値をそのまま外しても問題ない.そして k=1/2a と決めてやればずいぶん簡単になるだろう. r=a にあった特異点らしきものは消えた.特異点は r=0 に残るのみだ.これで気になっていたことが一つ解決である.

しかしこの結果はどうしたことだ.元の目的から逸れてはいないだろうか.我々は光の経路をグラフ上に 45°の直線で表したいと考えていたのだった.それなのに (8) 式からはいつものように光速を求めることができなくなっているではないか.

いや,大丈夫だ.分かりにくいかも知れないが,実に,その目標の直前に立っているのだ.

(8) 式で ds^2 =0 と置くと,とのいずれかは必ず 0 でないといけないことになる.つまり光の経路は (U,V) 平面のグラフ上において,まっすぐ上下方向,あるいはまっすぐ左右方向に引いた直線に限られるということになる.そこでもう一度確認するが,我々の望みは何だったか？光の経路を 45°の直線で表すことだ.それはもはや簡単ではないか.この座標のグラフを 45°回転させてやればいいだけである.

ちなみに,線素 ds^2 を (8) 式のような形で表せる座標のことを「ヌル座標」と呼ぶ.ヌル（null）というのは「ゼロ」とか「無」とかいう意味だ.二つの座標軸の方向がともに「線素がヌル」である光の経路を表しているからそう呼ばれるのである.

今考えている (U,V) 座標は「ヌル座標の形式のクルスカル座標」だというわけだ.これを 45°回転させたものも,やはりクルスカル座標と呼ばれるのである.

クルスカル拡張

グラフを 45°回転させるのはとても簡単なので後でやることにしよう.それよりも先にやっておくことがある.

ここまではシュバルツシルト半径の外側, r>a に限定した話だったではないか. 0<r<a ではどうなるのだろうか.

(6) の変換式を見れば読み取れると思うが, U=0 の線と V=0 の線はどちらも R=-∞ を表している.ということは, r=a を意味している.つまり,各象限を隔てる軸がシュバルツシルト半径を意味しているのである.（これがクルスカル座標に隠された工夫のひとつだ.）ブラックホールの内部はこれらの線に接した隣の領域にあるはずだ. (U,V) 平面には四つの領域があった. 先ほどまで計算していたのが右下の領域である.クルスカル座標を別の象限にも適用するために,変換規則を次のように拡張しよう. どれも最初の符号を調整しただけだ.秘密の小細工はどこにもない.

領域によって変換のルールを微妙に変えることに一貫性がないだとか人為的ではないかとか感じるかも知れないが,場合分けしないでひとつの数式で変換することにこだわるのは意味が無いことである.一般相対論ではたとえ作為的だろうが,奇妙に思えようが,どんな座標でも使って良いのだった.ただ気を付けないといけないのは,このような境界で計量の値が不連続になることがないようにするべきだということである.

ところがその条件は満たされている.上に並べたどの変換を使おうとも計算の内容には大差はなくて,(7) 式の右辺の最初の符号に違いが出るだけである.ところが r<a である故に絶対値の部分の計算で符号が逆転し,結局はどれも同じ (8) 式に行き着くことになるのである.というわけで,これらの変換を全て正当なものとして採用することにする！

あとはこの (U,V) 平面の全体を 45°左回転してやればいいだけだ.回転後の座標を (u,v) とすると, のようにすればいいのだが,縮尺を気にしなければ係数はこの通りでなくても構わない.今の状況では縮尺を気にしても意味がない.変換後の式が少しでも簡単になるように 1/2 は残しておこう. 下準備として次のような計算をしておく. 同様に, である.これらを使えば,ブラックホールの外側（右下の象限）ではという結果を得る.

次は右上の象限を考えてみよう.ここの領域はブラックホールの内側を表していると考えられるので r<a という前提で変形する必要がある.同じような繰り返しなので計算過程はざっと省いて,こんな感じになる. ルートの中身が少し違うのと,双曲線関数が入れ替わってるくらいの違いだ.

勢いで 4 つの象限を用意してしまったわけだが,左上と左下は何を意味しているのだろうか.どちらにしても,それぞれの境界でうまく接続するためには,先ほども説明したように (7) 式から (8) 式に無事にたどり着く必要がある.そのためには左上では r>a でないといけないし,左下ではブラックホールの内部と同じ r<a として計算しないといけない.

どれも符号に少しの違いがあるだけの似たような結果になるので省略しよう.

クルスカル座標の秘密

クルスカル座標への変換式には色んな工夫が隠されていると話したが,その最後の秘密をここで明らかにしておこう.最後の秘密というのは大袈裟だが,これを話せばもう他に特に言うことは残ってないよというくらいの意味である.

(6) 式をよく見ると,指数の肩の部分に, w+R という要素と w-R という要素が含まれている.すでに気付いているかも知れないが,実はこれは, (w,R) 座標を 45°回転するという意図があったのである.（じっくり考えると反転の要素も混じっているがそこは大して重要ではない.）

議論の流れを思い出すと,最初に我々は光の経路を 45°の直線で表したいと考えて (w,R) という座標を作ってみたのだった.それを 45°回転すれば,そう,ヌル座標になる.

(w,R) から (U,V) へと変換したときにヌル座標になったのは偶然ではなく,実は意図的に設計されたものだったというわけである.

グラフ化

この (u,v) 座標をグラフ化するのはそれほど難しくはない.その前に,45°回転のせいで「右下」とかの表現では分かりにくくなったので各領域に名前を付けておこう.

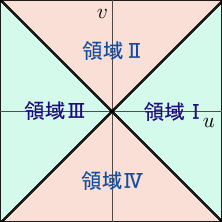
これまで「右下」と呼んでいた部分は今は右側に来ており「領域Ⅰ」とする.以降,左回りに「領域Ⅱ」,「領域Ⅲ」,「領域Ⅳ」とする.

例えば領域Ⅰを考えよう.(10) 式を組み合わせて双曲線関数の性質を利用してやると次のような式が作られる. これは双曲線の式であり,その形はの値によって決まる.つまり一定の線は双曲線によって表されるわけだ.

また,(10) 式からは次のような式も作られる. これは傾き v/u が一定の直線であり,その傾きはの値によって決まる.つまり時刻一定の線は直線によって表されるわけだ.

そのような考え方を他の領域にも当てはめて描いてみたのが次のグラフだ.

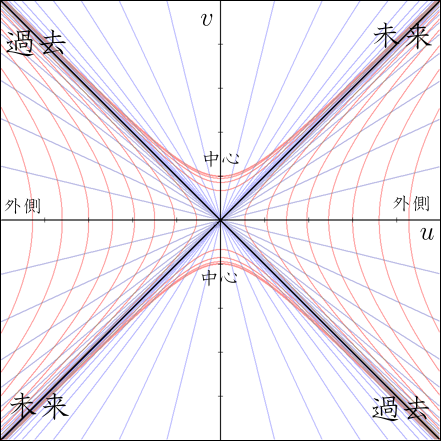
赤い双曲線が同一地点を表わしており,青い直線が同時刻を表している.

領域Ⅰはブラックホールの外側,我々の住む世界である.右へ行くほどブラックホールから離れることを意味する. v=0 の横軸が w=0 を表しており,下が過去で上が未来である.

領域Ⅱはブラックホールの内部である.上へ行くほどブラックホールの中心に近付くことを意味するが,あるところより上には赤い線がない.そこがブラックホールの中心 r=0 を意味している.そこより上の領域は (w,r) に対応しておらず,物理的な意味がない. u=0 の縦軸が w=0 を表わしており,それより右が未来で左が過去を表している.

領域Ⅲはブラックホールの外側であるが,我々の住む世界とは異なるどこか別の世界である.左へ行くほどブラックホールから離れることを意味する.なぜか上から下に向かって,つまり我々の世界とは逆に時が流れている.このような世界が本当に存在するかどうかは分からない.数学に頼りすぎて,現実にはありえない世界を作り出しただけかも知れない.

領域Ⅳは領域Ⅲの住人にとってのブラックホールの内部である.やはりそのようなものが存在するかどうかは分からない.しかし,もしあるとすれば,それは我々の世界とも境を接していることになる.そこからは物質粒子や光が飛び出してくる可能性があるが,内部へ入ることは許されない.ブラックホールとは逆の性質を持つというので「ホワイトホール」と呼ばれることになった.しかしホワイトホールから何かが飛び出してくるとすれば,それが飛び出したのは無限の過去の出来事に相当するわけだ.ホワイトホールが無限の過去から存在していない限りはそんなことはありえないのではなかろうか.

光の軌跡

ではいよいよ,出来上がったグラフを使って幾つかの事例について考えてみよう.そもそも,この目的のためにここまで苦労してきたのだった.

まずはブラックホールの外側にいる人が光を放った場合である.光の軌跡は次の図のように表される.

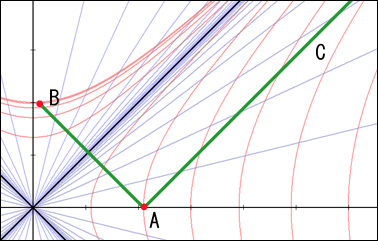
直線 AB はブラックホールの中心へ向けて発射した光の軌跡を表している.点 B はブラックホールの中心であり, r=0 である.光はシュバルツシルト半径を無事に通過して B にたどり着くことが分かる.図では時刻 w=0 に発射したことになっているが,どの時刻から始めても構わない.

ブラックホール内部での軌跡を見ると光は過去へと向かっているように読み取れる.光を発射する位置によっては,光を放った時点よりも過去へたどり着くということも起こり得る.とはいうものの,ブラックホールの中で何が起こっているかを知ることはできないので,このことで問題が起きることは決してない.この時間軸は飽くまでもブラックホールから無限に離れた場所にいる人にとっての時間であり,そう解釈できるというだけの話である.

一方,A から C に向かう直線は反対方向へ放たれた光の軌跡を表している.この直線は赤い双曲線と次々に交差し,時間の経過とともにブラックホールから離れる方向へ向かっていることが読み取れる.

物質はどうしても光よりは遅いので,どんなに頑張ってロケットエンジンを吹かしてみても,これら二本の軌跡に挟まれた領域内のコースを通ることになる.A からはブラックホールに入るコースを取ることもできるし,ブラックホールから離れるコースを取ることも出来る.もしその場にとどまる場合には赤い双曲線に沿ったコースを取ることになるだろう.この双曲線が位置一定の線を表しているというのはそういうことだ.

では次に,ブラックホール内部に落ちた人が光を放った場合のことを考えてみる.

D からブラックホールの中心方向へ放った光は E に到達する.放った時点から過去へ向かって飛んでいくという不思議なことになっているが,放った本人にはそのような感覚はないであろう.ここに描かれている座標は飽くまでもブラックホールの外側の解釈によるのである.

D から F への光はブラックホールの外側へ向けて放った光である.ところがこの到達点である F はやはりブラックホールの中心である.「そんなバカな！？」と思うかも知れないが,ブラックホールの中心へ向かった光も,その反対側へ向けて放たれた光も,いずれはブラックホールの中心へと到達する運命なのである.光より遅い物質は,E と F の間のいずれかの時刻に,やはりブラックホールの中心へと到達するであろう.ブラックホールの強力な重力がこのような不思議なことを引き起こすのである.

いやいや,信じられない.この結果を全力で疑ってみよう.

そうだ.このクルスカル座標では光の軌跡は 45°の直線で表されるということだった.しかしそれだけだ.どちらへ進むとまでは決まっていなかったのではないか？ひょっとしてシュバルツシルト半径の方へ向かって進む光だって許されているかも知れない.D からグラフの右下へ向かう光を考えてもいいのではないか？

しかしそのような線を書き込んでみた後で落ち着いて考えてみれば,これはブラックホールの外側からやってきてブラックホールの中心へと向かう光ではないか.先ほど考えた A から B へと向かう軌跡と全く同じ性質のものだ.この光はブラックホールの外側からやってきて D にいる人を照らすことになるだろう.

しかしやっぱりおかしい！前回の話で,ブラックホールの内部から外側へ向かう光はシュバルツシルト半径の内側ぎりぎりのところでいつまでもとどまるという計算結果を得たのではなかったか.そのような軌跡はこの図の中のどこにあるのだろうかと探してみると,やがて大変なことに気づいて愕然とする.それは先ほど考えた A から B へと向かう光線そのものなのだ.

A から無限の時間をかけてシュバルツシルト半径へと到達した光は,再び,今度は無限の時間を遡ってブラックホールの中心へと向かうことになる.この無限の時間を遡る過程が,外部にいる者にとっては逆回しに見える.まるで無限の時間をかけてシュバルツシルト半径に這い上がろうとしているように映るわけだ.しかしそれは我々がブラックホールの内部に向けて放った光に他ならない！

ああ・・・,何ということだ・・・.

計算では導けなかったのか

D から E に向かう光は A から B へ向かう光と同じ解であることは納得が行った.これについてはクルスカル座標を使わないでも,前回計算によって導くことができたのだった.少し誤解して,ブラックホールの中から這い上がってくる光だと解釈していたのだけれども.

では D から F へ向かう光は前回の話に出てきただろうか.それとも数式だけを使った方法では導くことのできないものだろうか？

いや,実は我々が見落としていただけで,これも数式として出てこようとしていたのである.ブラックホール内での光の軌跡を求める時,外側へ向かう光にだけ注目して,プラスマイナスの記号のうちからマイナスの符号だけを選んだことがあるのを覚えているだろうか？もしそこでプラスの方を選んでいれば次のような式が完成したはずである. これは前回の光の軌跡のグラフの横軸を反転させたものであり,定数を調整すれば次のようなグラフになる.

このように我々の時間での有限時間内にブラックホールの中心にまで到達することが数式からも分かる.もちろんブラックホールの内部を見ることはできないが.前回,この計算をしてみたとしても,割りと当たり前の結果だと受け止めるに終わったに違いない.

今回のようなクルスカル図の助けなしに,果たして我々はこのような奇妙で非常識な結果を理解し,受け入れることができただろうか.ブラックホール内に落ちた人が下向きに放った光も,さらには上向きに放った光も,そして本人も,いずれはブラックホールの中心に落ちてゆくなんて・・・.これを視覚的に受け入れさせるのがクルスカル図の効用である.

まだ疑う

ところでまだ疑いを持っている人がいるかも知れない.直線 DE と直線 DF が本当にブラックホール内にいる人にとっての上と下を意味するのだと断言できるものだろうか.ブラックホールの外にいる人の感覚と中にいる人の感覚は全く違っているのではないだろうか.

この疑問は私も持ったがやがて解決した.これがクルスカル座標のもう一つ面白いところだ.

我々は ds^2 というのが不変量であって,どんな座標で表現した場合にも変わらないようになっていることを知っている.また私の説明では ds^2 を表すときに一貫して座標時の方にマイナスを付けるように定義してきた.光の軌跡の場合は ds^2 =0 であったが,物質は光より遅いので dw^2 > dx^2 となる.だから必ず ds^2 <0 となるのである.

ところで,クルスカル座標 (u,v) を使った場合の線素 ds^2 がどう書けるのかをまだ計算していなかった.これは変換式 (9) の二つの式を辺々足し合わせたり,引いたりして, という関係が出てくるので, と計算できて,これを (8) 式に代入すれば次のように結果が得られる. ブラックホールの内部であろうとも,物質がたどるコースは ds^2 <0 を満たしているはずだ.そのためには必ず du^2 よりも dv^2 の方が勝っていなくてはならない.クルスカル図の中での移動を考える時,常に縦軸方向の変化の方が大きくなっていないといけないということを意味する.これにより,D にいる人が今後たどるコースは直線 DE と直線 DF に挟まれた領域でなければならないことがはっきりと分かるのである.これらの線が彼にとっての移動の限界を定めており,上と下を表すというわけだ.

ブラックホールの中では時間と空間の役割が入れ替わっていると説明する人がいる.外部の人の解釈を当てはめればそういう言い方もできるかも知れない.我々が時間の中を一ヶ所にとどまることができなくてひたすら未来へ向かって流れて行くのと同じように,ブラックホールに落ちた人は決して同じ位置にはとどまることができず,ひたすらブラックホールの中心へと向かうのである.その一方,僅かな範囲ではあるが彼らは時間を未来にも過去にも移動できるように我々には見える.彼らにとってはそのような感覚は全くなくて意味のない話かも知れないが.

そもそも強すぎる重力のせいで生きてなどいられない世界である.