相対性理論：水星の近日点移動

水星の謎

惑星というのは太陽を焦点の一つとした楕円軌道上を運行しているものだが,どれも普通の円と区別が付かない程度にしかひしゃげていない.水星は他より飛び抜けて離心率が大きい軌道を持つが,それでも長径と短径の比が 0.97 くらいであるから,やはり見た目は普通の円とほとんど変わらない.

離心率というのは,焦点位置が長軸半径の何割ほど中心から外れた所にあるかを示す数値である.水星の離心率は 0.2 くらいであるから,水星軌道の焦点の位置は円の中心から目立って離れたところにあることになる.図に描けば今話した事が一目で印象付けられるだろう.

太陽をちょっと大きく描きすぎたかも知れない.太陽の直径は水星軌道の直径の 1/83 程度であるから,直径 8 センチの円軌道を描いたときにやっと直径 1 ミリの粒に見えるくらいが本当だ.

その楕円の長軸の方向は常に一定なのではなく,長い期間の間に徐々にずれてゆく.太陽に最も近くなる位置を「近日点」と呼ぶのだが,それが移動すると表現しても良い.太陽から最も遠くなる点「遠日点」が移動すると考えても同じ事だが,なぜか「近日点移動」と呼ばれるのが普通である.分かり易く大袈裟に図に描くと,次のように綺麗な花模様が描かれて行くようなイメージである.

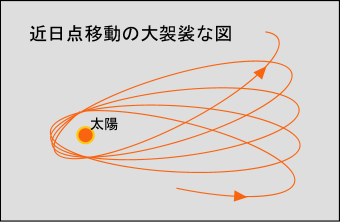
実際はこんなに目で見て分かる程度の動きではなく,ほとんど変化が無いと言っていいくらいだ.どれくらいのずれがあるかと言うと,水星の場合,100 年で僅か 574 秒なのである.ここでの秒とは時間の単位ではなくて,角度の単位である.1 度の 1/60 が 1 分で,そのさらに 1/60 が 1 秒である.つまり 1 秒というのは 1/3600 度.100 年で 0.16°くらいのズレしか起こらないということになる.それでも,そのような微妙な動きがあることが長年の観測によって明らかになっているのだから大したものだ.

そのズレの原因の大部分が,他の惑星からの重力の影響であるとしてニュートン力学の計算で説明できる.それもまた大したものである.ところが 574 秒の内の 43 秒だけがどうしても説明できないまま,19 世紀半ばから何十年もの間,ずっと謎として残っていたのだった.

今回はその 43 秒を相対論が見事に説明してのけた,という話である.この 43 秒という値には ±0.5 秒程度の誤差が含まれると見積もられているが,相対論の計算はその範囲内にしっかりと収まったのである.つまり今のところ,水星の近日点移動の謎は,もう謎ではなくなっているわけだ.

もし相対論のぼろを見付けたいならもっと精度を上げて確認しなければならないだろうが,そんな簡単に出来る話ではない.ニュートン力学による影響を算出するのに使った他の惑星の数値の妥当性も検証しなくてはならないし,影響を与えるものが本当に他にもないのか,あらゆる可能性を検討しなければならない.最近では銀河内での太陽系の運動が与える影響まで調べられているようだ.水星の運動の観測精度だけを上げさえすれば済むわけではない.

計算の方針

どのように考えて計算するのが最も分かり易くて楽だろうか.

水星は 88 日で太陽の周りを一周するのだから,100 年で約 415 回転してきたことになる.つまり一周するごとに約 0.104 秒ずつのずれが生じる事を示せればいいわけだ.

さて,ニュートン力学では惑星の軌道は次の式に従うことが分かっている. は太陽から水星までの距離の逆数で,は太陽を中心とした軸からの角度を表している.は離心率である.要するにこれは楕円の式であり,この式に従う限り近日点移動は起きず,水星は永遠に同じ軌道を回り続けるのである.

前回は測地線の方程式を u(φ) についての微分方程式の形にまで変形して行ったが,同じような方程式を導いてやれば上の式を当てはめて比較してやることが出来るだろう.ただし,今回求めようとしているのは光の軌跡ではないのだから,途中で光速の条件を入れることはしないで変形を続ける必要がある.

そうやって導かれた方程式に上の式をそのまま代入してやっても,きっと条件を満たさない.本当にごく僅かだが,上に書いた式から微妙にずれているはずなのだ.それがどれくらいずれていればその導かれた微分方程式に合うのかを調べてやればいいことになる.

方針としては以上だが,後で具体的な数値を入れるときのために,今の内に少しだけ補足しておこう.上の式にはという記号が使われているが,これは両辺ともちゃんと「長さの逆数」になってますよ,というのを分かり易く示すために使ったに過ぎない.この式で表される楕円について,長軸の長さを求めてやると, となる.理科年表などにはこの長さの半分の値である L/2 が惑星の「軌道長半径」として記載されていることが多いのである.

測地線の方程式

では,測地線の方程式を u(φ) の方程式で表す作業に取り掛かろう.前回「光の湾曲」の記事中でやった計算と途中までは同じである. θ=π/2 とするのも同じで,水星の公転軌道は平面上にあると考えて計算を楽にする.前回と違うのは,光速の条件を入れないようにする点だけである.

とは言うものの,前回は光速の条件によって式がかなり省かれたお陰で,あのすっきりした式にたどり着けたのだった.今回,それが無いのはかなり厳しい.何の工夫もなく変形を続けても係数がごちゃごちゃしてしまってまとまらないのである.先を説明する気が失せてしまうほどだ.

教科書を解読するのに手間取ったが,どうやらそれを回避する良い方法があるようだ.前回の途中の次の式からスタートしよう. 前回はこの式の第 2 項目が,光速の条件 ds^2 =0 を当てはめることですっきりと書き換えられたのであった.それに倣って似た事をやってみよう.今回は ds^2 =0 ではないが,と固有時の間には, - ds^2 = dτ^2 という関係があるのだったから,次のような式が成り立っている. ただし,は定数で, θ=π/2 , dθ=0 であることを代入済みである.この両辺を dτ^2 で割ってやれば, となるだろう.さあ,やろうとしている事に気付いただろうか.これまで何となく媒介変数としてを使ってきたが,ここでととを同一視してやるわけだ.そんなことをしても,もちろん良いのである.というのは測地線のコース上に目盛りを刻むものに過ぎないので,固有時の概念はその代わりとして十分に使える.

前回は光を扱っていたので,敢えてやらなかっただけなのだ.光については固有時の経過は常に 0 であると考えられるために,媒介変数に固有時という物理的解釈を与えることが出来なかった.

以上のことから, という条件式が出来上がる.これが (2) 式の第 2 項にピッタリ収まり,前回と似た変形を経て次の式が得られることになる. 今回もすっきりしてなかなかいい形をしている.これが光に限らないで,普通の物体にも成り立つ測地線の方程式である.時空が曲がっているので,測地線の中には太陽の周りを回り続ける軌跡を描くものもあるというわけだろう.

ところでこの式に含まれる定数は一体何を意味するのだろうか.もしこの定数が今後の計算結果に最後まで残るような場合には,これに何らかの値を代入してやる必要があるからちょっと気になる部分だ.

その心配はあまり要らないのだが,取り敢えず説明しておこう.そもそもこの定数が登場したのは,前回求めた次のような式の積分定数としてであった. 今回はとを同一視しているので,微分は惑星の運動の角速度を意味することになる.つまりこの式は r×rω=h ということだから,これは,ケプラーの法則の一つである「面積速度一定」を表しており,もし両辺に惑星の質量を掛けたなら,角運動量保存則を意味している.しかし今はその値が具体的にどうなるかは考えないでおこう.

ずれを調べる

では先ほど話した計画を実行していくことにする.(1) 式はこのままでは (3) 式を満たさないだろう.しかし前回と同じ理由で (3) 式の右辺第 2 項を無視してやった場合には,(1) 式がそのまま当てはまることが確認でき,ついでに次の関係式が得られる. これを使えば後での値を考える必要がなくなるだろう.このように,(3) 式の右辺第 2 項は相対論的な補正を表しており,それがない場合にはニュートン力学的な運動を表す式になっていることが分かる.

ところが (3) 式の右辺第 2 項を有効にした場合には,ニュートン力学の解に僅かな変更が加わるだけのはずなので,それを次のように表してやろう. これを (3) 式に代入してやれば χ(φ) についての微分方程式が得られる.それを解いてやればいいだろう.・・・などと考えていたが,それは甘い考えだった.はごく小さい関数だと仮定したにも関わらず,の増加に伴ってどこまでも増加を続ける解が出て来てしまって,前提を崩してしまうのだ.

実はこれは非線形微分方程式を解く時には良く起こる問題であり,解くためにはちょっと技巧的なことが必要になってくるのである.

非線形微分方程式の問題

ちょっと相対論から離れて,方程式を解く事に集中しよう.今後の説明が分かりやすいように,(3) 式を簡単な形に書き直しておこう. 実はこれは,バネに吊り下げられて振動するおもりの運動方程式に似た形になっている.質量 m=1 で,バネ定数 k=1 で,おもりに掛かる重力 mg=A といった状況だ.ただし右辺第 2 項にはおもりの変位の 2 乗に比例する項があって,このバネの力がわずかにフックの法則からずれている状況を意味している.おもりがどちらへずれても一定の方向に力が掛かるのはちょっと変であり,この手の問題を扱っている教科書ではの 3 乗の項が使われているのが普通だ.だから残念ながら,教科書から結果だけをもらって来て,「詳しくはその手の教科書を探して調べて欲しい」などと書く事は出来ない.

しかし心強い結論が書いてあった.バネがフックの法則に従わなくなるほど振動が激しくなると,・・・それは右辺の第 2 項のようなものが無視できないほど効いて来るという意味だが・・・,そうなると振動の周期が元の状態からずれるというのは良く知られていることらしい.バネの問題ではは時間の関数なので周期がずれるという結果として現象に表れるのだが,今回の問題ではは回転角の関数なので,前と同じ角度だけ回っても同じ状態には戻ってこないという意味になるだろう.数式の上では似たような問題であるようだ.

非線形微分方程式というのは,それを解くための決定的な手続きというのが存在しないと言われている.それで,過去の経験の蓄積による技巧に頼らざるを得ないことを受け入れてもらいたい.今,が 0 の場合の解 $u_{0}$ は, だとしておく.このは (4) 式の右辺に使われていると同じ定数値で,は別の任意の定数値だ.そしてが 0 から徐々に増加して行く時,解の方も元の状態 $u_{0}$ から徐々にずれるのだろうが,そのずれ方が,に比例する項,の 2 乗に比例する項などの和で表されると考えてみよう. しかし ε^2 というのはとても小さいので,それ以下の項は無視してしまおう.さらに少々の技巧を施して,結局,次のような仮定を採用することにする. に依存する項を cos 関数の中にも追加しておくことにしたわけだ.なぜここには ε^2 に比例する項を入れなかったかというと,それは cos 関数をテイラー展開したものを考えてやれば分かる.その影響は,すでに無視されている ε^2 以下の項と同程度に過ぎないから,一緒に省かれたということだ.

これを (4) 式に代入してやると,次の式を得る. ただし計算途中で ε^2 以上の項が出てきた場合には全て排除してある. cos 関数の中にあったはずのが消えているのもそのためで, εcos[(1+ε)φ] という形が出て来た時点で ε^2 に比例する要素を排除して εcosφ と置き直したのである.

この式を解いて未知関数 $u_{1}$ の形を決定したいのだが,これはまたまたバネの問題とそっくりになっている.しかし非線形の項がないのが救いだ.右辺の全ての項は外力の存在を表している.これにはただ一つの問題があって,右辺の第 3 項はバネの振動周期と同じタイミングでの揺さぶりを掛けることを意味している.外力の中にこのような成分が含まれていて他にブレーキをかける要因がない場合には,共鳴を起こして振幅 $u_{1}$ が際限なく大きくなってしまうことが知られている.そのような解は前提に反するし,欲しくないのである.この問題を避けるためには k=-A であれば良いだろう.そうすれば第 3 項は完全に消えてなくなり,次のように,簡単に解けることになる. 結局つじつまの合う形の (4) 式の近似解は, となるというわけだ.

結論

以上の話を (3) 式に当てはめればいい. であるので, となる.後ろの方に付いて来た項は第 1 項に比べて無視してもいいくらいだと分かって一安心だ.気になるのは最初の項の cos 関数の中身に加わった変化だ.これが軌道にどんな影響を与えることになるだろう.

近日点は今の場合, cos 関数が -1 となるところだ. cos 関数の中身を見ると,に 1 よりごく僅かに小さな係数が掛かっている形になっているので,水星が一周して φ=2π となっても cos 関数は -1 に戻らないことになる.ほんの僅かだがだけ余分に回ってやらないといけない.このことを式で表すとこんな感じか. 細かなところは切り捨ててこれを解くと, となる.これが欲しかった答えだ.定数は結局残らなかったか.後はこれに具体的な数値を入れるだけでよい.

水星の離心率		0.20563
水星の軌道長半径		0.3871 (天文単位)
1 天文単位	-	149,598,700,000 (m)
太陽のシュバルツシルト半径		2953 (m)

ラジアンは,360 × 60 × 60 秒だから,の代わりに 360 × 60 × 60 を使えば,秒単位の値で答えを出せる.

(参考)気になる方は,コピペして Google の電卓機能なんかでご確認ください.
今回の計算値 = 360 * 3600 * 3/2 * 2953/ (1-0.2056^2)/(149598700000 * 0.3871)
シュバルツシルト半径 = 2GM/c^2 = 2 * 6.67300e-11 * 1.98892e30 / 299792458^2

この結果,0.1035 秒という答えを得る.始めに宣言しておいた数値とは少し違っているが,415 を掛けて 100 年分の数字に直すと,42.9 秒という値が出る.ちゃんと誤差の範囲だ.

少し言わせて欲しい

世の中には相対論が完全に間違っていると考えている人がいて,仲間を増やそうと大々的に宣伝を行っているのを良く見かける.

しかしそういう人たちは,相対論に代わってこの数値を説明できるだけの代案を示さなくてはならないことになる.それは非常に難しい事だろうし,無駄な努力に終わる可能性の方が高いだろう.それに賭けたのならば,人生を捨てる覚悟で相当頑張ってもらわないといけない.

いや,彼らが頑張っているのは知っている.しかし相対論に反対するキャンペーンの方ばかり頑張ってもらっても,人生を棒に振る人が増えてしまってとても心配になるのだ.

私のところにもそういうロビイストたちがコンタクトを取ろうとしてくる.「間違った理論に騙されている私」を救おうとして,熱心に説いてくる.その気持ちは本物だが,彼らの説く内容は幼稚で穴だらけ,矛盾だらけである.私がその不備や勉強不足を指摘しても,彼らは私の頑なさに失望し,私のことを憐れみながら去って行くのである.

私もまた彼らを憐れんでいる.彼らが自身の勉強不足を棚に上げて,自分こそは正しいと信じ切っている高慢さに.