前回と今回のつながり
前回は孤立系を考え,全体としてエネルギーが一定不変である状態を想定した.今回の本題に入る前に,もうしばらく孤立系を考え,その中の小部分に注目してみよう.
熱平衡が実現している状況では系の全体がほぼ均質になっているとは言える.しかし,エネルギーが全体に一様に分布しているとまで考える必要はない.そのような制限はしていないのだが,結果としてほぼ均質な状態が実現しているのである.各微小部分に目を向けると,平均値を中心にして上下にわずかなエネルギーの揺らぎがあると考えられる.
ところで熱平衡とは何だったろうか?私に学問的に厳密な言い方を期待しないで欲しいのだが,要するに,2 物体が熱のやり取りをした結果,温度が等しくなって,それ以上の熱のやり取りがなくなったように見える状態である.いや,実はそうなった後でも熱エネルギーのやり取りは続いているのだが,それを時間的に平均して見ると 0 に見えるのである.
一時的ならば・・・,それはつまり一瞬ならばという意味だが,2 物体のうちの一方が平均よりエネルギーが高くなっても構わない.もちろんその分,他方のエネルギーは平均より低くなっているわけだ.それでも我々はこの状況を「2 物体の温度は等しい」と呼ぶのである.温度とエネルギーを同一視できないことが分かるだろう.
話は 2 物体に限らない.これと同じように,孤立系が平衡に達して,全体が一定の温度であると考えられるとき,それでも,その内部の微小部分にはエネルギーが高い部分も低い部分もあり得るわけだ.そのエネルギーの揺らぎは捉え所の無いようなパターンで出現するのだろうか.それとも何らかの規則が見出せるのだろうか.今回はそういう話を考えていこう.
温度についての再確認
ここに来て,はて?では温度とは何だっただろうか,と記憶をたどり直す人もいることだろう.熱力学ではカルノーサイクルの動作を基準にした「熱力学的温度」というものを定義した.しかしこれは学問的に都合がいいように決めたやり方であって,イメージしにくいものであると私も思う.
統計力学ではこれより分かりやすいイメージが出てくることになるのだが,それはまだ説明していない.ただ,理想気体に限ってはの式により,粒子の 1 自由度ずつに分け与えられる平均エネルギーと関係ある量のようだと説明しただけである.だから温度について漠然とした理解しかできていないという気持ちがあったとしても今のところはそれほど心配は要らない.
しかしちゃんとした定義も無いまま,漠然とした感覚だけに頼って話を進めているのではないことに注意しておこう.今のところ,熱力学から借用してきた
という式などを頼りにして議論を進めているのである.一応,こういう議論の土台は熱力学の方にちゃんと持っているということだ.
温度一定の系
今回考えるのは,次のようなモデルである.
前回と同じように体積と粒子数
は一定だが,容器全体が恒温槽に浸されており,エネルギーについては恒温槽とのやり取りがあるとする.もはや孤立系ではないわけだ.代わりに温度は常に外部と同じであり,
で一定だとする.
系のエネルギーが一定でないということは,もはやガンマ空間内の等エネルギー面には縛られていないということである.では今回は,ガンマ空間全体の状態数を数えることになるのだろうか?いや,そんなことをしても何の意味もないだろう.そもそもガンマ空間はエネルギーに上限がない限りは無限に広がっているのであり,状態数を数えようとしてみても際限がないのであるから.
さらに等重率の原理も使えそうにない.等重率の原理はリウビユの定理を基にしているのだった.そしてリウビユの定理は正準方程式を使って導いたのだった.その説明の時には特に孤立系でなくても成り立つと書いたが,それは例えば外部磁場などの影響があっても構わないという意味であって,ハミルトニアンが定義できれば問題ないということだ.ところが今回のような場合にはハミルトニアンが時間によってどう変化するのかは表しようがないのである.
だから,等エネルギー面の制限がなくなったからといって,あらゆるエネルギーの状態が平等に現れることができるだなんて,そんなおかしな考えに飛躍してはいけない.
等重率の原理が使えないとなると,他に使えそうな手は残されていないように思えるのだが,これで一体何ができるというのだろうか.これはもう前回とは全く違った話になっているではないか.
等重率の原理を使う
ところが少し見方を変えると,これは前回の話とそっくりなのである.説明しやすいように,先ほどの図と同じ状況を別の配置で描き換えてみよう.
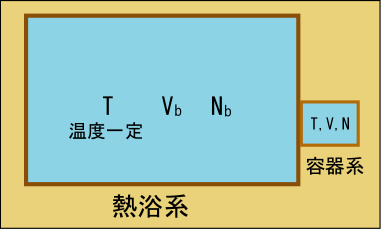
左の大きな容器が恒温槽を表しており,右側の小さな容器が今考えている系である.恒温槽と呼ぶと,電気などを使って温度を一定に保つ装置を思い浮かべてしまうが,今は話を単純化したいので,代わりにもっと原始的なものを考えておこう.つまり,気体の詰まった,ただの巨大な容器である.それは右側の容器に比べてあまりに巨大なので,右側の容器との間で少々のエネルギーをやり取りしたところで温度は少しも変化しないとする.
説明しやすいように,今後は左側を熱浴系,右側を容器系と呼ぶことにしよう.
さて,前回の話とどこが似ているかというと,熱浴系と容器系をひっくるめた全体系は,孤立系ではないか.そして,容器系というのは,その中の微小部分に過ぎないというわけだ.今回の冒頭の話が表していたのはこのことだったのである.しかしこの状況にどうやって数式を当てはめたら話が進むのだろう.
まず,全体系のエネルギーをだとしよう.全体では孤立系になっており前回と同じことが言えるので,全状態数
が計算できるはずだ.その全ての状態の中で,容器系がエネルギー
を持つ状態というのは,一体,幾つほどあると考えられるだろうか.
それはこう考えればいい.容器系と熱浴系の間でエネルギーの交換ができるのは,互いの系の間に相互作用があるお陰であるが,その相互作用のエネルギーは全体から見れば無視できる程度であると考えることにしよう.つまり,お互いの容器の中の粒子間で強い引力や斥力が働いたり,化学反応を起こしたりすることはないということだ.こういう仮定をしておけば,それぞれの容器をそっと引き離したり,そっと触れ合わせたりしても,なんらの影響もないことになる.
今,たまたま容器系がエネルギーを持っているとしよう.すると熱浴系の方は
のエネルギーを持っていることになる.この時,二つの系をそっと引き離したとしたら,それぞれの系は孤立系だと考えられる.そして,前回やったようにそれぞれの状態数を数えることができる.孤立系では状態数というのは
,
,
の関数であったのだから,容器系のみの状態数は
であるし,熱浴系のみの状態数は
という形で表されるであろう.そしてこれらの積こそが,容器系がエネルギー
を持つ時の場合の数だということになる.よって,全体から見た割合は,次のように表される.
なかなか面白くなってきただろう.ところで熱浴系のエントロピー
は,ボルツマンの関係式に
を代入して得られるはずである.
面倒なのでこの式ではエネルギー以外の変数は省略している.この式の左辺を近似することを考えよう.容器系が持つエネルギー
というのは全体のエネルギー
と比較してごくごくわずかだと考えられるので,次のような変形が可能である.
ここで (1) 式を使ったのである.さらに変形を続けよう.
これを (3) 式の右辺と比べてみれば,
となっていることが分かる.つまり (2) 式は,次のように書けることになるのである.
ここでも相変わらず熱浴系の変数
,
は省略されたままだが,そもそも熱浴は全体の温度を
に保つために導入されたものであって,それ以外のパラメータは仮に使ってきただけの定数に過ぎない.よって今後はもう顔を出すことはないだろう.
ところで (4) 式は確率を表しているのだから,許されている範囲の全てのエネルギーについて積分してやったものは 1 にならないといけない.
(4) 式の右辺の分数の部分には変数
は含まれていないので,この部分はもはや単に (5) 式を成り立たせるための規格化定数の意味しか持たないことになる.つまり,(4) 式は次のような実にシンプルな形に表すことができるわけだ.
うーん,いや,これは少しおかしいな.次元が合っていないのが気になる.(6) 式は無次元なのに,(5) 式の左辺でそれをエネルギーについて積分した結果が無次元になるというのは良くない.(6) 式は次のように書き直しておくべきだろう.
エネルギーに揺らぎがあるときにはエネルギーが厳密にちょうど
になるなんてことはないのだから,幅を持たせて考えないといけないのだった.
の範囲に含まれる微視的状態の数を
と表すことにした.
のことを「状態数密度」と呼ぶ.こうすれば (7) 式は (6) 式とさして意味が変わらないし,容器系がエネルギー
を持つ確率という意味になるわけだ.
分配関数
しかし (7) 式が得られたところでこれが一体何の役に立つというのだろう.前回やった「小正準集団の方法」では,全ての状態数を数え上げるのが難しいから応用が利かないと話したのだった.ところがこの式に含まれる
というのは,それを
で微分しただけのものであって,手間は何も変わらないことになる.これでは何の改良にもなっていないではないか.
そうなのだ.実はこの話はもう少し続けないといけないのだが,思っていたより話が長くなってしまった.今回は切りのいい結論まで導いて,具体的な使い方は次回に送る必要がありそうだ.
とりあえず,こんなことを考えてみる.(7) 式に含まれる定数を導きたいと思ったら,まず次のような計算をする必要があるだろう.
この
の逆数が定数
を意味することになる.
で積分するのだから,結果からは
は消えてしまって,
,
,
の関数して表されることになる.この計算結果をわざわざ関数
と名付けて表しているのは,これがこの後で非常に重要な意味を持つことになるからだ.この関数を「分配関数」と呼ぶ.
ところがこの (8) 式はもっと簡単な式で表せそうなのだ.というのが,「エネルギーが
の範囲にある微視的状態の数」を表していた.それに因子
を掛けながら,全てのエネルギーに渡って連続的に足してゆくのである.つまりこれは,あらゆる許された微視的状態について,次のような足し算を実行することに等しいと言えるのではないだろうか.
ここで
は,容器系がある微視的状態
にあるときの,容器系の全エネルギーを意味している.この計算は,エネルギーの値が何であろうと関係なく,容器系の全ての微視的状態について因子
の値を計算しては足し合わせて行くことを意味するのである.
この (9) 式の形で表現された分配関数は量子力学的な考え方を当てはめるのに特に便利な形式であり,「状態和」と呼ぶことがある.また因子は今後も頻繁に出てくることになるが,これを「ボルツマン因子」と呼ぶ.
よくある誤りについて
この分配関数には一体どのような意味があるのだろうか.すっきりした式なので何か直観的な解釈が出来そうな気がするが,今はやめておいた方がいいように思う.冷淡な態度のように思うかも知れないが,これは規格化定数を決めるための計算に過ぎないのだ.
教科書によってはこれを「ボルツマン分布」と呼ばれるものに関連付けて説明されることが良くある.確かに関連はあるのだが,しかしあまり先を急ぐと誤解を招くことがあると思うのだ.例えば,次のような怪しげな説明が世の中にごろごろしているのだが,目にしたことはないだろうか.
| ある温度 |
これは間違っているとは言い切れない文だが,これだけでは解釈を誤らせる可能性がある.全エネルギーがであるような微視的状態の出現確率は,(7) 式で表されるのであり,単純に
だけに比例するのではないからだ.
さらに加えて,この説明だと,ボルツマン分布というのがエネルギーごとの粒子数分布を表していて,その形がであるかのように思えてしまうが,実際はそうではない.正しくは,相空間内の微小な一定範囲に粒子が見出される確率を表しているのだ.これについてはちょっと難しいから,後でボルツマン分布の話をするときに詳しく説明しよう.
それでも上の説明は間違いだとは言い切れない.紛らわしいことだが,ボルツマン分布に従っている集団のものであれば,それがエネルギー分布だろうが速度分布だろうが,どんな形のグラフであろうが,ボルツマン分布と呼ぶことがあるからだ.
しかし文脈をたどっていくと,説明している側でさえ誤解しているようだったり,これでは必ず誤解を誘うだろうというような書き方になっている説明に,時々出くわすのである.
それでも少し考えてみる
直観的解釈とまではいかないが,ボルツマン因子が出てくる理由を少し考えてみよう.
エネルギーが 0 のとき,ボルツマン因子は 1 となり,エネルギーが増加するに従って徐々に 0 へと近付いて行く.小正準集団の方法では,全ての微視的状態の出現確率はどれも等しいと考えたのだった.因子は常に 1 だった,という考え方も出来る.しかし今回は,エネルギーによって出現の度合いが差別されるのである.
もちろん,あるエネルギーが実現する確率はエネルギーだけで決まるのではない.同じエネルギーに属する微視的状態の数が多ければ,そのエネルギーが実現する確率は増すであろう.しかし単純な数の大小だけでは決まらないということだ.一体何がそうさせているのだろう.
今回の式変形を見ていくと,原因は容器系の方にあるわけではない事が分かる.容器系がエネルギーを取るときに,その
の値が増えれば増えるほど,熱浴系の方ではその状態を実現するための「場合の数」が減るのである.その減り方が,ボルツマン因子として現れているだけなのだ.熱浴も含めた「場合の数」を,容器系に属するパラメータ
で表現しようとしてこうなるのである.
ではなぜ,それが指数関数になるのか.それは今回の式変形をもう一度見てもらうことにしよう.私なりに簡単にまとめれば,エネルギーが全体に比べてごくわずかであるとき,エントロピーの変化が
であることが熱力学から要請される.その変化と状態数の変化の比率はボルツマンの関係式で結ばれているから,熱力学の要請を満たしてつじつまの合うように調整したらこうなったというわけだ.










