さっさと行こう
今回はフェルミ粒子についての話である.前回のボース粒子と対比して話をしようと思うが,内容はほとんど同じなので,一部を変更するだけでいい.違う部分だけ話してなるべく短く終えることにしよう.
大正準集団を使う
大正準集団を使えば楽であるというところまで,ボース粒子とほとんど同じである.ボース粒子では次のような分配関数を考えればいいという話になっていた.
しかしフェルミ粒子の場合には一つの一粒子状態に入れる粒子はただ一つのみなので,0 個であるか,1 個であるかのいずれかを考えればいいことになる.つまり上の式の
の部分を 1 に書き直しただけの次のようなものを考えればいい.
途中の式変形も前回と同じように進むだけなので省略.
ここからが少し違う.前回は無限等比数列の和の公式を持ってきたが,今回は 0 から 1 までの和なので,そんなものは必要なくて,単純に次のように 2 つの項に展開して書いてやればいい.
当然なのか偶然なのか,ボース粒子の場合ととてもよく似た形になっている.
フェルミ・ディラック分布
このを使ってグランドポテンシャル
を求めると,
となる.ボース粒子の場合とちょっと符号が違うだけの差である.これを使って
を求めると・・・途中の計算は前回と似たようなものなので省略しても構わないだろう・・・次のようになる.
符号が一箇所違うだけであって,ボース粒子の場合とそっくりの形ではないか.この意味は,やはりボース粒子の場合と同じである.つまり,各状態
にある粒子の個数が,平均して
となっていると解釈できるということだ.しかし今回は
の範囲については何の制限も必要ないようだ.その振る舞いは後でもっとよく調べることにしよう.
こののグラフの形をそのままの意味で粒子数分布であると考えてはいけないという注意点は今回も同じだ.これを次のような関数
として表したとき,これを「フェルミ・ディラック分布」と呼ぶ.
式の符号が一箇所違うだけなのに,このグラフはボソンとはかなり様子が違っていて,面白い特徴がある.
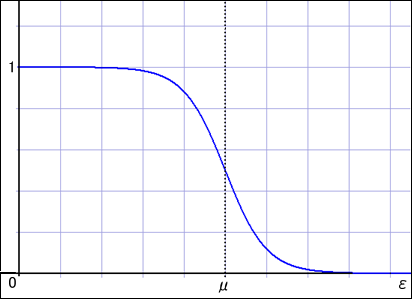
まず,最大値は 1 を超えない.この関数は各状態に存在する粒子の平均個数を表しているのだった.フェルミオンは同じ状態に 1 個以上は入れないのだからこうなって当然である.当然ではあるが,ちゃんと関数がそのルールを守ってくれているのが面白い.そして,エネルギーがに近くなるところまで上がって行くと,存在確率が急激に減少して 0 に近付く.
この急落の度合いは温度によって大きく変化し,が 0 近くになると,次にあるグラフのように,あるところまでは 1 で,それ以上のエネルギーにある粒子数は 0 だという具合に境目がはっきりしてくる.
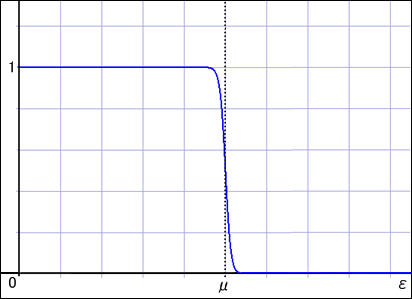
これはつまり,こういう意味だ.粒子はエネルギーの低い状態から順に詰まってゆく.フェルミオンは同じ状態には二つ以上の粒子が入れないので,後から来た粒子はどんどんエネルギーの高い方へと入るしかない.そして,入るべき粒子が全て入り切ってしまうと,それ以上のエネルギーを持つ状態に入る粒子はもうない.
ところが温度が上がってくると,一番高いエネルギー状態に入っている粒子から徐々に,さらに高いエネルギーを持つ状態へとジャンプし始める機会を得ることになる.温度が上がればかなりの数の粒子がこのジャンプに参加できるようになるので,グラフの形の角の部分がなまり始めるというわけだ.
このように,多数のフェルミ粒子の集団は絶対零度にあってもかなり高いエネルギーを持っていることが分かる.絶対零度の状態で,低いエネルギー準位から一つも抜けがなく全ての粒子が詰まっているときに,一番高いエネルギーに入っている 1 粒子のエネルギーのことを「フェルミ準位」または「フェルミエネルギー」と呼ぶ.
化学ポテンシャルとその斥力的作用
これらのグラフを見れば,化学ポテンシャルがどんな値を持っているべきかがおおよそつかめるだろう.それは絶対零度においてはフェルミエネルギーに等しいのである.
しかしながら,はボソンのときと同じく,(1) 式を満たすための規格化定数の役割を果たしているのだから,温度が変化すればそれに合わせて微妙に変化するだろう.一方,フェルミエネルギーは定義からして,温度によって変化するような性質のものではない.
温度が上がったときにはの値は上がるのか,それとも下がるのか.それは今持っている条件だけでは何とも言えない.(1) 式の
が一定になるように振舞うのは確かだが,それはこのグラフの積分値が一定になるという意味とは違うからだ.各エネルギー準位
がどのように分布しているかによって決まるだろう.
しかしとにかく,フェルミオンの化学ポテンシャルはかなり大きな正の値であることだけは確かだ.それはつまり,粒子が加わるときにエネルギーが余分に必要であることを意味している.だってそうだろう.絶対零度のときでさえ,フェルミエネルギーくらいのエネルギーがないことには,この集団には参加することができないのだから.それでフェルミオンの集団というのは,粒子間に特に相互作用がない場合であっても,あたかも斥力的な作用が存在するかのような振る舞いをするということになる.それについての具体的な話はまたいつかしよう.










