統計力学：ボソン

今回の話が長くなった理由

ここでは,ボース粒子を扱うときにおおよそ共通して出くわすだろう事柄について,大雑把にまとめることをしようと思う.これから話すのは考え方のヒントのようなものであって,ここで採用した方法以外にもやり方は色々とある.しかし基本的な疑問さえ解決させて頭を整理しておけば,すべてを網羅する必要はないと思うのだ.

最初にぶつかる大きな問題は,「小正準集団」か「正準集団」か「大正準集団」か,どのアンサンブルを選んで説明したら良いかという問題である.

前にも話したように,実はどの方法を使っても同等であって,ただ問題に応じた使いやすさによって使い分ければいいのである.そして,結論を先に言ってしまえば,粒子を識別できない量子統計の場合には「大正準集団」を採用するのが断然,便利なのだ.

しかしその便利さを実感してもらう為には,別の方法の不便さや限界というものを知ってもらう必要もある.というわけで,他の方法を試してみるという寄り道もしてみよう.

小正準集団の場合

小正準集団で扱うときの基本は,系全体の (N,E,V) を一定だと考えることだった.今,全粒子数がだとして,どれも同等であるとする.同等であるから,どの粒子もそれぞれに, $s_{1},s_{2},…$ という色んな状態のいずれかになることが同じように許されているとしよう.

状態が決まればエネルギーが決まる.ある粒子が番目の状態 $s_{q}$ である時のその一粒子のみのエネルギーを $ε_{q}$ だとしよう.もちろん,状態が違ってもエネルギーの値が同じだということはある.粒子の状態というのはエネルギーだけで決まるものではないからだ.の添え字が違えば別の状態にあるのだと考えることにする.

全ての粒子はどの状態でも取りうるわけだが,一つだけ制限があり,全エネルギーが一定でなければならない.式で書くと次のようになる. ここで番目の粒子が番目の状態にあることを表すために q_i という表現を使っている.本当は粒子を区別しないようにしたいので番目の粒子などという区別はまずいのだが,言っている意味が伝わるようにとりあえず表現してみた.

とにかく,このような条件を満たすような状態の組み合わせを考えつつ,しかも任意の粒子を入れ替えた組み合わせも全く同じものだと考えて,重複して数えることを避け,さらに複数の粒子が同じ状態にある場合についても考慮して,すべての組み合わせを間違いなく求めるというのは,かなりの工夫が要る.

少し前の「プランクの理論」という記事では,上手い具合にさりげなくそれを実行しているのである.いや,これはかなり幸運なケースだろう.なぜそんなことが出来たのか,少し復習してみようか.

もうほとんど忘れているかもしれないが,あの時は,ある周波数だけに反応する共鳴子というものを考えて議論の範囲を絞るのに成功しているのである.どんな種類の共鳴子がどれだけずつ存在するかは,他の論理に任せたのだった.それで,やり取りするエネルギーは全てであるという簡略化したイメージが使えたのである.

それで全エネルギーを同一の個の粒に分けるという考え方が使えた.ここで言う全エネルギーとは「ある周波数だけに反応する共鳴子の群れ」だけが持つ全エネルギーという意味なので,全周波数から見れば一部のエネルギーなのである.とにかく,これで,全エネルギーの条件を満たしつつそれを分配することが楽になった.そしてそれを個の共鳴子に分配する分け方の数は幾つであるかを考えたのだった.これがまさに,起こりうる全ての状態を重複なく数えることに相当しているのである.

プランクは粒子が区別できるかどうかという点には注目していなかった.ただ統計力学の基本的な考えに忠実に,実現し得る状態の数を正しく数えただけなのだが,要するにそれでいいのである.

教科書によってはラグランジュの未定乗数法を使うことで,状態数を重複なく数えるという面倒な内容をうまくやっていたりする.気になる人はそういう流儀の教科書を探してみて欲しい.このサイトでは最初からその手法を使ってこなかったこともあり,今更紹介するのも冗長な気がして何となく気が引けているのである.

正準集団の場合

ここまでの話は,全エネルギーの制限があると非常にやりにくい,というだけの話である.では,正準集団の考えを使えば全エネルギーを気にする必要もなくなるので,もう少し具体的な話に踏み込めるだろうか.

正準集団の方法というのは,とにかく全ての起こり得る状態についての次のような和を計算して分配関数（状態和）を求めてやろうというのが基本である.後はそこから色んな熱力学的な量が求められるのである. 全エネルギーについての制限を考慮する必要は無くなったが,相変わらず,全ての起こり得る状態というものがどんなもので,どれだけあるのかということは考えないといけない.

それで,さっきと同じようにこのように考えたらどうだろうか.今,全粒子数がだとして,どれも同等であるとする.同等であるから,どの粒子もそれぞれに, $s_{1},s_{2},…s_{M}$ という色んな状態のいずれかになることが同じように許されているとしよう.

ここで,1 番目の粒子が状態 $s_{q_1}$ に,2 番目の粒子が状態 $s_{q_2}$ にある・・・と考えて, という計算をすれば,全ての組み合わせを考慮することが出来そうだろう.いや,確かに全ての組み合わせは表現できているのだが,粒子の入れ替えについては何も考慮されておらず,かなりの数え過ぎになってしまっているのである.

そこで考え方を大きく変えることにしよう.

その前に・・・,今回の話では「状態」という言葉に複数の意味があって,さっきからどうも紛らわしいなぁ.混乱しないようにちゃんと呼び名を分けておこう.まず, $s_{1},s_{2},…s_{M}$ のように,粒子の一個一個がそれぞれ取り得る状態のことを「一粒子状態」と呼ぼう.そして個の粒子の一粒子状態の組み合わせによって決まる全体の状態のことを「系全体の状態」とでも呼ぶことにしようか.これですっきりするだろう.

話を続けよう.一粒子状態 $s_{1}$ にある粒子の数は $n_{1}$ 個であり,一粒子状態 $s_{2}$ にある粒子の数は $n_{2}$ 個であり・・・,という具合に,粒子に番号を振らずに,各一粒子状態を取る粒子の数で系全体の状態を指定するのである.こうすれば全エネルギーは, と表せるだろう.各一粒子状態には,最大で個の粒子までの粒子が入るだろうし,全く入らないこともあるから,次のように表現すれば全ての系全体の状態を表現できるだろうか. いやだめだ.これでは全ての一粒子状態に個の粒子が入っているというような,有り得ない状態まで数えてしまっている.全粒子数がなのだから次のような条件が満たされていないといけない. なかなか難しいな.これを無理やり (2) 式に取り入れようとすれば,クロネッカーのデルタ記号でも使って, としてやるしかないだろうか.条件に合う項だけ選んで加えてやる,という意味に過ぎないので,数式で表したからといって根本的な解決になっていないのは分かっている.

粒子数の制限のない大正準集団を使えばこんな問題は回避できるのだが.

ところで「光の粒子説」という記事の中で紹介したアインシュタインによる固体の比熱の計算のところでは正準集団の考え方を使っており,しかもプランクの理論と全く同じ式を導く結果となっているので,この節の話と非常に関係があるのではないかと思えるかも知れない.しかしあれは,全く同じ意味の計算をしていながらも,その思考の前提が全く違うのである.それについては少し後の記事で説明しようと思う.

大正準集団の場合

これで大正準集団の手法を使う理由が分かっただろう.この手法を採用する場合には,粒子数の制限も考えずに次のような状態和を作ってやればいいのであった. これを今の問題にあてはめてみよう.先ほどの (2) 式では 0～N の和を取っていたが,この手法の場合にはもう無限大まで和を取ってやって構わない.またこの式のの部分には今回も (1) 式を使えばいいし,の部分には (3) 式を使ってやればいい. この式はもっと簡単に書き直すことが出来る.指数関数の中で和を取っている形になっているので,積の形に分解してやるのである. これは同じ形式の積になっているので, (…)^M という形にまとめてやりたい気はするのだが,残念ながら $ε_{1},ε_{2},…ε_{M}$ はそれぞれ値が異なっているので,そういう形には出来ない.それで,次のような積の記号を使って省略表記するのがやっとだろう. ところが,この和の記号の部分を見ると,初項が 1 で,公比が $exp\{-n_m (ε_m -μ)/kT\}$ の無限等比数列の和になっており,有名な公式を当てはめることが出来るのである.いや待てよ？その公式は公比の絶対値が 1 未満だという条件付きで使えるのだったから, ε_m -μ>0 でないとまずいな.その点は問題ないだろうか.熱力学を振り返って探してみてもその辺りの明確な根拠は見当たらないように思える.しかしそもそもこの条件が満たされていないことには発散してしまって計算を続けることも出来ないのだから,とりあえずこれを認めてしまうことにしよう.これについては後でちゃんと解決することになるから心配しなくてもいい. 比較的すっきりした形にまとまって一安心だ.

ボース・アインシュタイン分布

折角だからこのを使って,熱力学関数を求めることを試してみよう.グランドポテンシャルは次のように求めるのだった. これを使って S,p,N などを求め,さらに F,U を求めることができるというのは前に大正準集団を紹介した記事の中で説明したが,ここでは話の流れ上,マクロな意味での粒子数を求めることを優先しよう. さあ,この結果はどういう意味であろうか.各一粒子状態にある粒子の個数が,平均してとなっているという具合に解釈できそうだ.いや,たまたまそのような関数の和の形でが表されるというだけで,実際にそういう分布になっているわけではないのではないかと疑う人は,この解釈の正当性を別の方法で試みることも出来る.以前に導き方の手順は示してあるので途中の計算は省略するが,を求めたならば, という結果を得るはずだ.これを見たら $<n_{m}>$ の解釈はほぼ決定的になるだろう.さらに,さまざまな実験結果が,この解釈を裏付けている.

$<n_{m}>$ が粒子の数を表しているというのだから,(5) 式は必ず正の値でなくてはならないはずだ.そのためには $exp\{(ε_m -μ)/kT\}>1$ でなければならず,そのためには全ての ε_m に対して ε_m >μ となっていなければならない.もし ε_m の一番小さいところの値が 0 だとすれば, μ<0 でなければならないということだ.これはボソンの場合にはそういう条件が付くということであり,フェルミオンの場合にはまた別の話になる.これで先ほどの無限等比数列の和の公式の条件の話は解決したと言えるだろう.

さて,この $<n_{m}>$ というのが各エネルギーごとの粒子数分布を表しているらしいというので,それをグラフに表したらどんな形になっているのだろうというところに興味が出てくるだろう.これからそれを描いてみるつもりだが,それを見るときには少し気を付けた方がいいとあらかじめ言っておこう.

なぜなら (4) 式の中の ε_m というのは一粒子状態ごとに決まるエネルギー値であり,連続に存在するものではないし,の数が進むたびに一定のエネルギー幅ごとに増えるものだとも限らないからだ.数限りないほど多くの異なる一粒子状態がどれもほぼ同じエネルギー値を取るように密集しているということもあり得る.だから,ボース粒子の集団がいつだって,これから示すグラフのような形のエネルギーごとの度数分布をしているのだと考えるべきではない.

この注意点は,以前に「正準集団（前編）」という記事の後ろの方の「よくある誤りについて」という節で話したことと共通していると言えるだろう.

ラグランジュの未定乗数法を使う流儀の教科書では,あるエネルギー範囲に存在する状態数というのをあらかじめ導入して計算することで,その辺りの効果をうまく吸収させた上で,同じ式を導き出すに至るのである.私はこれが何を意味しているのか把握できずに結構苦労したのだった.

それでも参考までにこの関数の形を視覚的に把握しておきたいと望むならば,物理的イメージとはひとまず分けておいて,ただのそういう関数として受け入れるか,大雑把な傾向として捉えておくのがいいかも知れない. この関数 f(ε) のことを「ボース・アインシュタイン分布」と呼ぶ.

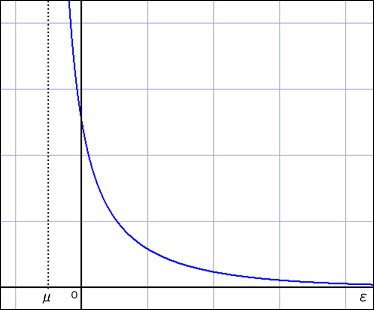
この関数は横軸がとなるところで発散してしまうのだが,ボソンの場合はが基底状態より低い値になっているはずなのでそこは問題にならない.参考までにが負になる領域まで描いておいたが,物理的には何の意味もない.

化学ポテンシャルとその引力的作用

先ほどの値に制限があることを話したが,このの値は固定されたものではなく,温度や粒子数や体積の関数になっている.すると,それはどんな形の関数なのかと思うだろう.

もう一度 (4) 式を見てほしい.ここではの値が決まることによってが計算できるような形になっているわけだが,実のところというのは,この式の結果がとなるように調整するための規格化定数のような役割を果たしている存在なのである.

だいたいの傾向として,が増えればも増えるし,が 0 に近付けばは増える,というくらいのことは読み取れる.系の体積との関係は読み取れないが,それは各 ε_m を通して間接的に入ってきていると言える.各 ε_m は与えられた条件によってどうとでも決まるものなので,それが具体的に定まっていないことには何とも言い難い.

先ほどのグラフで,を 0 に近付けてゆくと,すべての粒子はエネルギーの低い状態へと集中し始める形になることが分かる.グラフを積分した面積は粒子数を直接表すものではないが,粒子数の傾向をおおよそ表すものであり,それは大変小さくなって行く.それを補うために,が徐々に右側へ出て来なくてはならないことが分かるだろう.

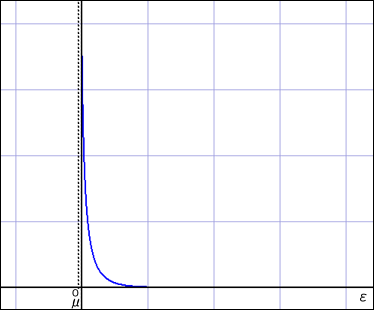
しかしながらは単なる規格化定数としてだけ存在しているわけではない.これには化学ポテンシャルという意味があり,それは体系に粒子を一つ加えるために必要なエネルギーを表しているのだった.それがマイナスであるということは,粒子を取り除くときにエネルギーが要るということを意味する.つまり,ボソンの集団には粒子間に特に相互作用がない場合であっても,何か引力的な作用が存在するかのような振る舞いをするということである.それについてはまた今度,実例を使って説明することにしよう.

プランクの理論との関係

どのアンサンブルを使って考えても同等だという話だったので,大正準集団を使ったここまでの結果とプランクの理論との間にも深い関連があるはずだ.しかしプランクの導いた結果にはは出て来なかった.どう考えたら今回の話にプランクの理論を当てはめることが出来るだろうか.

まず,光の粒をボソンだと考えるわけだ.エネルギーがであるような光の粒子が $1/(e^{(ε-μ)/kT}-1)$ 個だけ存在するというのが今回の話の結論である.そのエネルギーがであれば,その合計のエネルギーはと表されるということで,が入っていることを除いてはプランクの理論と一致する.ところで,光子が取り得るエネルギーはただ一つではない.空洞内では周波数が 0 から（ほぼ）連続的に存在するのだから,光子のエネルギーも同じようにほぼ連続的に存在する.上の方でしてきた話ではボソンが取り得る各エネルギーとして $ε_{1},ε_{2},…$ というような離散的なものを考えたわけだが,連続的に存在していると考えてもイメージは大して変わらない.和を取る代わりに積分をすることになるだろう.周波数幅の範囲ごとに,つまりエネルギー幅 h dν ごとに, (8πν^2/c^3) dν 個ずつの状態が存在するということになる.(4) 式との対応を比較するために書けば, という感じになるだろうか.この式は思い付きで書いてみただけで具体的に計算するつもりはなかったのだが,気になるので試しにやってみた.（少し前の「ちょっと幾つかの確認」という記事でやった計算テクニックが役に立った.）するとどうやらが存在することが原因で発散してしまうようである.では μ=0 にすれば問題ないかというと,今度は温度が増えるに従って,粒子数が幾らでも増えるという結果になってしまう.その無数の粒子は一体どこから来たのだろうか？

それは元からあったと考えるのはどうだろう.エネルギーが 0 というのは光子がない状態のことではあるが,光子が「エネルギー 0 の状態にある」と表現しても問題ない.つまり,エネルギー 0 の光子が元から無数に存在していて,高いエネルギー状態に飛び上がる出番を待っているというイメージなわけだ.先ほどは積分を使ったので,一番低いレベルに集中している大量の粒子の存在が計算上はほぼ無視される結果となったのである.

粒子の数が元から無限大あるとなれば,が 0 でなければならないというのも説明が付くだろう.実際,光子は生まれたり消えたりするのに,以外のエネルギーのやり取りは必要ないわけで,化学ポテンシャルが 0 だという話とも辻褄が合う.

こんな具合にして,光子も一種のボソンだというイメージで説明されるのである.