今回の記事でやろうとしていることは単純である.前回導いた式に具体的な数値を入れてみて,実際にどんなことが起こっているのかを確認しようという,それだけだ.
速さの分布は次のように表せるのだった.
この
のところに水素分子の質量を代入したものをグラフにすると次のようになる.
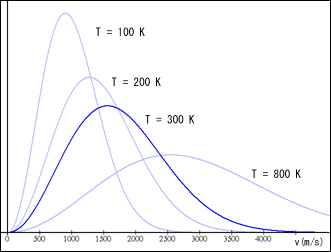
300 K(約 27℃)での分子速度のピークでの値を読むと,1600 m/s にもなる!私はこれをグラフ描画ソフトに描かせているのだが,初め何も考えずにに「水素原子」の質量を代入してしまい,その結果,おおよそ知っていた速度に比べて速すぎるところにピークが来たので首を傾げてしまった.ああ,そうだ.ちゃんと分子を考えないとな.
こういうグラフを自分で描いてみると,色々と気になることが自然と出てくるものだ.例えば,温度を上げていくと,ピークは右へ右へと移動する.しかし一定の数値ずつ温度を上げていっても,ピークの右移動は徐々に鈍ってくる.どうしてそういうことになるのだろう?いや,理由は別に気にしていない.そこにはどういう関係があるかということだ.
またここでは最も軽い例として水素分子を選んでグラフにしてみたが,水素ガスというのは日常的にはあまり馴染みがない.馴染みがあると言えば,空気の大部分を占める窒素ガスだろう.窒素分子の質量は水素分子と比べてかなり違う.質量がこれだけ違うと,分子速度のピークはどう変わるのだろう.そんなことはグラフを描いてみればすぐに分かるのだが,似たようなグラフばかり並べるのも能がない.
分子の種類ごとの違いをどう表すのが読者にとって分かりやすいだろう.例えば,ピークの速度を表にしておくだけで十分だろうか.それだけでグラフの特徴が全て伝わるものだろうか.例えばピークの速度を知っただけで,グラフの裾野が右へどの程度伸びているかということまで分かるものだろうか.
要するに,わざわざ毎回 (1) 式を使わなくても,フリーハンドでかなり正確にグラフの形を再現できるようなテクニックがもしあるのなら,それを提供してみたいと思うのだ.(興味が物理とは関係ない方へ逸れてきた.)
ピークでの速度値
まず,グラフの極大点を求めるくらいは簡単だ.高校の知識で出来る.
意外とすっきりした式だ.これだけのことで,先ほど気になった幾つかの問題は一気にクリアだ.グラフのピークは,温度がケルビン単位で
倍に増えても
倍にしかならないと分かる.
また,分子の質量が倍になると,ピークは
倍のところに下がる.窒素分子の質量は水素分子の約 14 倍だから,
で,約 430 m/s となる.
それでもまだずいぶんと速いものだな.そんな高速の分子が目の前を飛び交っているわけだ.いや,我々自身,常にそれらの衝突を受けているのだ.一体,1 秒に何回くらい,他の分子と衝突しているのだろう?それに,どれくらいの距離,他の分子と衝突しないで直進できるのだろう?それはまた別の機会に考えることにしよう.
分子の平均速度
ところで,グラフのピークのところだけ読み取って,それが分子の速度だと言ってしまうのも強引だろう.その速度よりも速い分子もあれば,遅い分子もある.せめて平均速度くらいは計算しておくべきではなかろうか.
それを計算するのも容易いことだ.(1) 式は分布を表しており,積分すれば 1 になるように規格化定数もつけてあるのだから,これにを掛けて積分するだけで平均値が算出できる.
ここでは「良く使う積分公式」の中の (4) 式を利用している.
この結果を見ると,平均速度というのは,先ほどのピークの速度値
よりも常に
倍大きいというだけのようである.
グラフの着地点
あと気になるのは,グラフが原点からピークまで駆け登った後,どの辺りに着地するように描けばもっともらしいか,という点だ.グラフは無限遠まで伸びていて,厳密にはどこまで行っても着地することはないので,何か他に,グラフの特徴をつかむいい方法を考えないといけない.半値幅とか,変曲点とか,標準偏差とか・・・何に頼るのが一番いいだろう?
色々と試してみたが,どうもあまり面白くない.それでこんなことを考えてみた.グラフが横軸に付きそうな点を求めるのである.(1) 式を無限まで積分すれば 1 になるようにしてあるのだから,どこまで積分すれば 0.99 になるかを調べてやればいい.
しかし (1) 式を積分するという,こういうガウス積分と呼ばれるものは,無限遠までなら積分値が正確に求められるのだが,途中までの積分値は初等関数では表せないというのである.仕方が無いからパソコンで数値積分して,おおよそどの辺りで着地するかを求めてやった.
試行錯誤して,0.99 ではなく 0.999 までにした方が,よりグラフと合うと分かった.例えば,水素分子の場合,T = 100 K で 2532 m/s,T = 200 K で 3581 m/s,T = 300 K で 4386 m/s といった具合だ.グラフと見比べると,ちょうどその辺りでほぼ横軸に接するばかりとなっている.つまり 99.9 % の粒子はこの速度以下だということだ.
こんなことは他の教科書ではわざわざやっていないが,これをほぼ「最高速度」だと判断しよう.さて,この最高速度は温度や粒子の質量によってどう変わるだろうか?数値を変えて計算させて確かめてみた.結果を知ってしまった後では当たり前だと思えるのだが,温度が倍になると
倍になるし,質量が
倍になると
倍になるのである.グラフは横に引き伸ばされても形の比率そのものは変わらないというわけだ.
しかしこれを覚えておけば,グラフをフリーハンドで描いたりするのに役に立つだろう.水素分子で T = 300 K の場合,最頻値が約 1600 m/s であり,ほぼ最高速度である約 4400 m/s はその約 2.8 倍だ.この比率は変わらない.これで気になっていたことが解決したことになるだろう.
この 2.8 倍という数値に何らかの学問的意味があるのかって?いや,ないだろう.99.9 % という数字に何の意味もないのと同じだ.










